数学九年级上册1 菱形的性质与判定备课ppt课件

这是一份数学九年级上册1 菱形的性质与判定备课ppt课件，共13页。PPT课件主要包含了菱形的定义，菱形是轴对称图形，菱形的四条边相等，条对称轴就是对角线，互相垂直，又∵ABAD，∵OBOD，∴AO⊥BD，即AC⊥BD，∵∠BAD60°等内容，欢迎下载使用。
观察下面图形，有什么共同特征
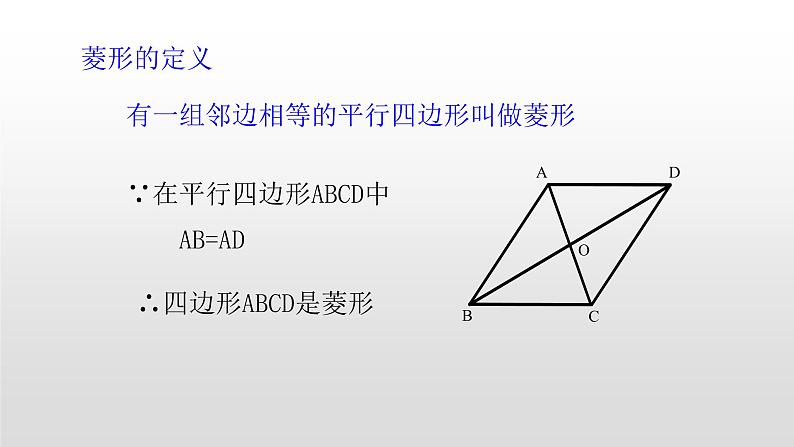
有一组邻边相等的平行四边形叫做菱形
∵在平行四边形ABCD中 AB=AD
∴四边形ABCD是菱形
用菱形纸片折一折，回答下列问题:
( 1 )菱形是轴对称图形吗?如果是，它有几条对称轴?对称轴之间有什么位置关系?
(2)菱形中有哪些相等的线段?
菱形的四条边相等，对角线互相垂直
已知:如图，在菱形ABCD中，AB=AD,对角线AC与BD相交于点O.
求证: (1 ) AB= BC=CD=AD; (2) AC⊥BD.
证明: (1)∵四边形 ABCD是菱形,
∴AB=CD, AD= BC (菱形的对边相等).
∴AB= BC= CD= AD.
(2)∵AB= AD,
∴△ABD是等腰三角形.
又∵四边形ABCD是菱形,
∴OB= OD ( 菱形的对角线互相平分).
在等腰三角形ABD中，
例1如图，在菱形ABCD中，对角线AC与BD相交于点0,∠BAD=60°，BD=6，求菱形的边长AB和对角线AC的长.
解：∵四边形ABCD是菱形，
∴AB= AD (菱形的四条边相等),
AC⊥BD(菱形的对角线互相垂直),
OB= OD= BD = ×6=3 (菱形的对角线互相平分).
∴△ABD是等边三角形.
在Rt△AOB中，由勾股定理，得
OA2+ OB2= AB2
∴AC= 20A= 6 (菱形的对角线互相平分).
菱形的性质(重点、难点)归纳
(1)菱形具有一切平行四边形的特征.
(2)菱形的对角线互相垂全等的直角三角形,往往与勾股定理相联系.
(3)菱形是轴对称图形,每一条对角线所在的直线是它的对称轴.
(4)若菱形的内角有60°(或120°)时，图中含有等边三角形或含30°角的直角三角形.
练习1.如图,已知菱形ABCD的对角线相交于点0,延长AB至点E,使BE=AB,连接CE.(1)求证:BD= EC;(2)若∠E=60°,求∠BAO的大小.
(1)证明:∵四边形ABCD是菱形，
∴四边形BECD是平行四边形，
∴∠BAO=∠DCA =30°.
∴AB = CD,AB//CD,
∴BE= CD, BE//CD.
(2)解:在口BDCE中，∠E =60°,
∴∠CDB = 60°.
2.菱形的周长是16 cm,两邻角之比为1:2,求菱形的两对角线的长.
解:∵两个邻角之比为1:2,
由菱形的性质得AC⊥BD
DO=0B、A0=CO.
∴∠DAO =30°,
作业布置：习题1.1 1，2，3,4
1.如图,已知菱形ABCD中,E、F分别是BC、CD上的点,且∠ B=∠EAF=60°, ∠BAE=18°,求 ∠CEF 的度数.
∴60°+ 18°= 60°+∠CEF,
∵四边形ABCD为菱形，
∴△ABC与△CDA为等边三角形.
∠B=∠ACD=∠BAC=60°.
∴∠BAE=∠CAF.
∴△ABE≌△ACF.
又∵∠EAF= 60°
,∴△EAF为等边三角形,
∴∠AEF= 60°,
∴∠AEC=∠B+∠BAE=∠AEF+∠CEF.
∴∠CEF= 18°.