


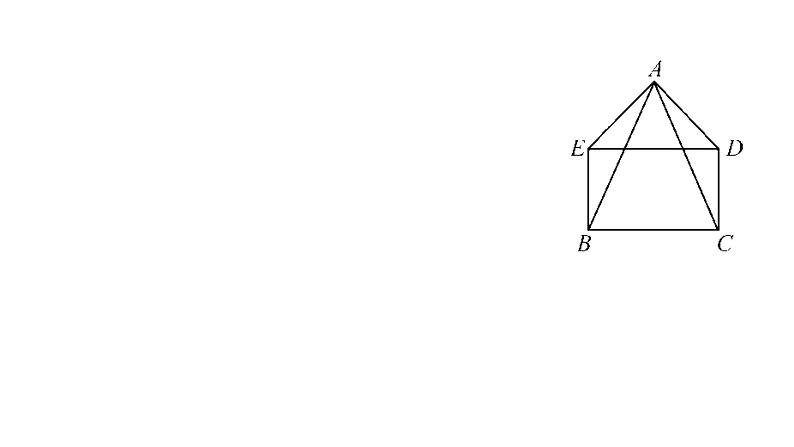



所属成套资源:2020九年级数学上册课件北师大版()
北师大版九年级上册2 矩形的性质与判定课文配套课件ppt
展开
这是一份北师大版九年级上册2 矩形的性质与判定课文配套课件ppt,共43页。PPT课件主要包含了∴□ABCD是矩形,在△ABC中,∴AD⊥BC,∴∠ADC90°,又∵CE⊥AN,∴∠CEA90°,作业布置,选讲习题,∴∠BAD=90°,证明∵MN∥PQ等内容,欢迎下载使用。
例3 如图,在矩形ABCD中,AD=6,对角线AC与BD相交于点O,AE⊥BD,垂足为E,ED=3BE,求AE的长.
解:∵四边形ABCD是矩形,
(矩形的对角线相等且互相平分),
∠BAD=90°(矩形的四个角都是直角).∵ED=3BE,∴BE=OE.∵AE⊥OE,∴AB=AO.∴AB=AO=BO,即△ABO是等边三角形.∴∠ABO=60°,
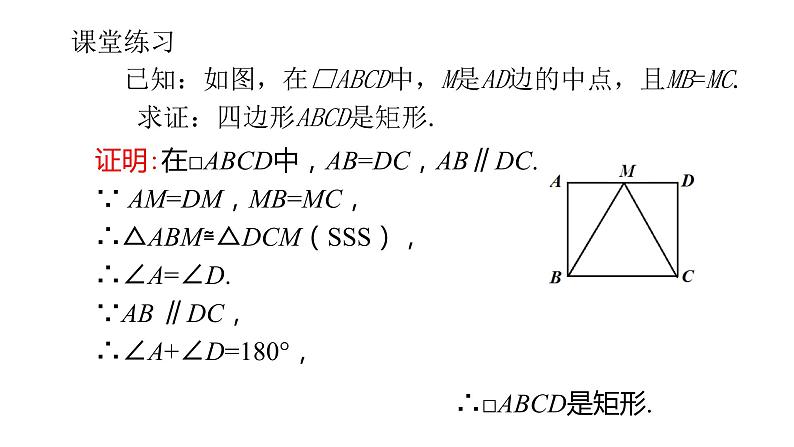
课堂练习 已知:如图,在□ABCD中,M是AD边的中点,且MB=MC. 求证:四边形ABCD是矩形.
证明:在□ABCD中,AB=DC,AB∥DC.∵ AM=DM,MB=MC,∴△ABM≌△DCM(SSS),∴∠A=∠D.∵AB ∥DC,∴∠A+∠D=180°,
例4 已知:如图,在△ABC中,AB=AC,AD是△ABC的一条角平分线,AN为△ABC的外角∠CAM的平分线,CE⊥AN,垂足为E.求证:四边形ADCE是矩形.
证明:∵AD平分∠BAC,AN平分∠CAM,
∴四边形ADCE是矩形.(有三个角是直角的四边形是矩形)
∵AB=AC,AD为∠BAC的平分线,
习题1.5 1,2,3,4
1.如图,已知MN∥PQ,AB、CB分别平分∠MAC、∠PCA,AD、CD分别平分∠NAC、∠QCA.求证:四边形ABCD是矩形.
∴∠MAC+∠PCA=180°.
∵AB、CB分别平分∠MAC、∠PCA,
∴∠BCA+∠BAC=90°,
∵∠MAC+∠CAN=180°,AB、AD分别平分∠MAC、∠NAC,
∴四边形ABCD是矩形.
2.如图,四边形ABCD是矩形,△PBC和△QCD都是等边三角形,且点P在矩形上方,点Q在矩形内.求证:(1)∠PBA=∠PCQ=30°;(2)PA=PQ.
证明:(1)∵四边形ABCD是矩形,
∴∠ABC=∠BCD=90°.
又∵△PBC是正三角形,
∴∠PBC=∠PCB=60°,
∴∠PBA=∠PCD=30°.
又∵△QCD是正三角形,
∴∠PCQ=∠QCD-∠PCD=30°
∴∠PBA=∠PCQ=30°
(2)∵CD=CQ,CD=BA,
又∵∠PBA=∠PCQ=30°,
∴△PAB≌△PQC,
3.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连接BF交AC于点M,连接DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE∶S△BCM=2∶3.其中正确的结论有( )A.4个B.3个C.2个D.1个
【典例2】如图,在Rt△ABC中,∠ACB=90°,DE为△ABC的中位线,∠CEF=∠A.(1)求证:四边形CDEF是平行四边形;(2)若AC=4,BC=3,求四边形CDEF的周长
解答:(1)证明:∵∠ACB=90°,D为AB的中点,∴CD=AD,∴∠A=∠DCA.∵∠CEF=∠A,∵DE为△ABC的中位线,∴DE∥BC,∴DE∥CF,∴四边形CDEF是平行四边形.
∴∠DCA=∠CEF,
4.如图,在矩形ABCD中,AC、BD交于点O,延长BC到点E,使CE=BC,连接AE交CD于点F.若AD=10,求OF的长.
6.(南宁中考)如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.(1)求证:AE=CF;(2)若AB=6,∠COD=60°,求矩形ABCD的面积.
7.如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD,BE,BC于点P,O,Q,连接BP,EQ.(1)求证:四边形BPEQ是菱形;(2)若AB=6,F为AB的中点,OF+OB=9,求PQ的长.
(2)若AB=6,F为AB的中点,OF+OB=9,求PQ的长.
8.(达州中考)如图,在△ABC中,点O是边AC上一个动点,过点O作直线EF∥BC分别交∠ACB,外角∠ACD的平分线于点E,F.(1)若CE=8,CF=6,求OC的长;(2)连接AE,AF.问:当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
(2)解:当点O在边AC上运动到AC中点时,四边形AECF是矩形.理由如下:连接AE,AF,当O为AC的中点时,AO=CO,∵EO=FO,∴四边形AECF是平行四边形,∵∠ECF=90°,∴平行四边形AECF是矩形
9.如图,在▱ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.(1)求证:四边形BECD是平行四边形;(2)若∠A=50°,则当∠BOD=_________时,四边形BECD是矩形.
10.如图,四边形ABCD中,对角线AC,BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.(1)求证:四边形ABCD是矩形.(2)若∠ADF∶∠FDC=3∶2,DF⊥AC,则∠BDF的度数是多少?
(1)证明:∵AO=CO,BO=DO,∴四边形ABCD是平行四边形,∴∠ABC=∠ADC,∵∠ABC+∠ADC=180°,∴∠ABC=∠ADC=90°,∴四边形ABCD是矩形(2)解:∵∠ADC=90°,∠ADF∶∠FDC=3∶2,∴∠FDC=36°,∵DF⊥AC,∴∠DCO=90°-36°=54°,∵四边形ABCD是矩形,∴OC=OD,∴∠ODC=54°,∴∠BDF=∠ODC-∠FDC=18°
11.如图,在▱ABCD中,点P是AB边上一点(不与A,B重合),CP=CD,过点P作PQ⊥CP,交AD边于点Q,连接CQ.(1)若∠BPC=∠AQP,求证:四边形ABCD是矩形;(2)在(1)的条件下,当AP=2,AD=6时,求AQ的长.
(1)证明:∵∠BPQ=∠BPC+∠CPQ=∠A+∠AQP,又∵∠BPC=∠AQP,∴∠CPQ=∠A.∵PQ⊥CP,∴∠CPQ=∠A=90°.又∵四边形ABCD是平行四边形,∴四边形ABCD是矩形
12.如图,在△ABC中,AC=3,BC=4,AB=5,点P在AB上(不与A,B重合),过P作PE⊥AC,PF⊥BC,垂足分别是E,F,连接EF,M为EF的中点.(1)请判断四边形PECF的形状,并说明理由;
解:(1)四边形PECF是矩形.理由:在△ABC中,AC=3,BC=4,AB=5,∴AC2+BC2=32+42=52=AB2.∴∠ACB=90°.∵PE⊥AC,PF⊥BC,∴∠PEC=∠ACB=∠CFP=90°.∴四边形PECF是矩形
(2)随着P点在边AB上位置的改变,CM的长度是否也会改变?若不变,求CM的长度;若有变化,求CM的变化范围.
【典例2】如图,在Rt△ABC中,∠ACB=90°,DE为△ABC的中位线,∠CEF=∠A.(1)求证:四边形CDEF是平行四边形;(2)若AC=4,BC=3,求四边形CDEF的周长分析:(1)由直角三角形的性质,得CD=AD,则∠A=∠DCA,等量代换得到∠DCA=∠CEF,故DC∥EF.又由中位线性质得到DE∥BC,即可得证;(2)求出DE、DC的长,即可得到四边形CDEF的周长.
13.如图,矩形ABCD的对角线交于点O,点E是矩形外一点,AE∥BD,BE∥AC.(1)如图1,求证:四边形AEBO是菱形;(2)如图2,当∠ADB=30°,连接CE交BD于点F,连接AF,若BE=2,求AF的长度.
14.如图,△ABC中,D是AB上的一点,连接CD,DE平分∠BDC交BC于点E,DF平分∠ADC交AC于点F,如果AD=BD=CD,求证:四边形CEDF是矩形.
15.如图,将□ABCD的边AB延长到点E,使BE=AB,连接DE,交边BC于点F.(1)求证:△BEF≌△CDF;(2)连接BD、CE,若∠BFD=2∠A,求证:四边形BECD是矩形.
16如图,在矩形ABCD中,AB= ,BC=3,在BC上取两点E、F(点E在点F左边),以EF为边作等边三角形PEF,使顶点P在AD.上,PE、PF分别交AC于点G、H.(1)求△PEF的边长;
相关课件
这是一份北师大版九年级上册2 矩形的性质与判定教课内容ppt课件,共17页。PPT课件主要包含了一个内角是直角,几何画板,对边平行且相等,对角相等邻角互补,对角线互相平分,是中心对称图形,∠B90°,∠ABC90°,又∵BEED,∴EAEC等内容,欢迎下载使用。
这是一份初中数学北师大版九年级上册2 矩形的性质与判定教学课件ppt,文件包含第1课时矩形的性质pptx、第2课时矩形的判定pptx、第3课时矩形的性质与判定的综合运用pptx、平行四边形的变化mp4、旋转矩形mp4、活动框架mp4、矩形大小不断变化mp4、矩形轴对称mp4等8份课件配套教学资源,其中PPT共61页, 欢迎下载使用。
这是一份初中北师大版第一章 特殊平行四边形2 矩形的性质与判定课文ppt课件,共20页。PPT课件主要包含了导学一,自主探究,矩形的性质,四个角都是直角,对角线相等,邻边互相垂直,例题解析,巩固训练,合作竞学,3对角线等内容,欢迎下载使用。










