初中数学北师大版九年级上册3 正方形的性质与判定示范课ppt课件

这是一份初中数学北师大版九年级上册3 正方形的性质与判定示范课ppt课件，共22页。PPT课件主要包含了如图沿AA′剪开得到，做一做，∴AD⊥AB，解得x5，作业布置，选讲内容，∴AEEC，∵BC10cm，∵EF∥BC，前面和右面剪开等内容，欢迎下载使用。

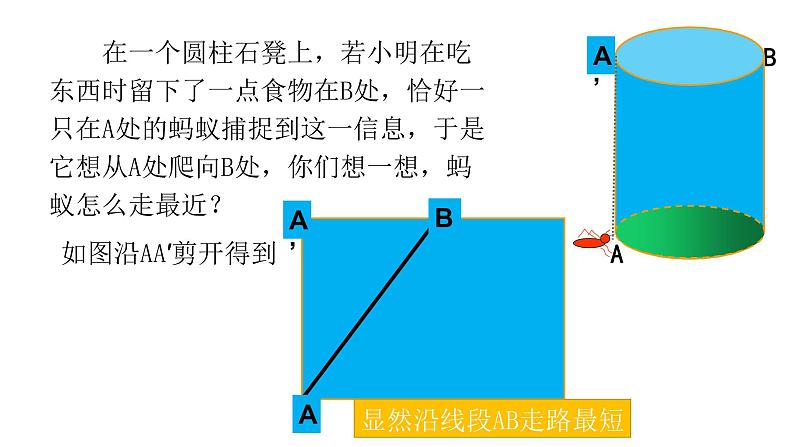
在一个圆柱石凳上，若小明在吃东西时留下了一点食物在B处，恰好一只在A处的蚂蚁捕捉到这一信息，于是它想从A处爬向B处，你们想一想，蚂蚁怎么走最近？
显然沿线段AB走路最短
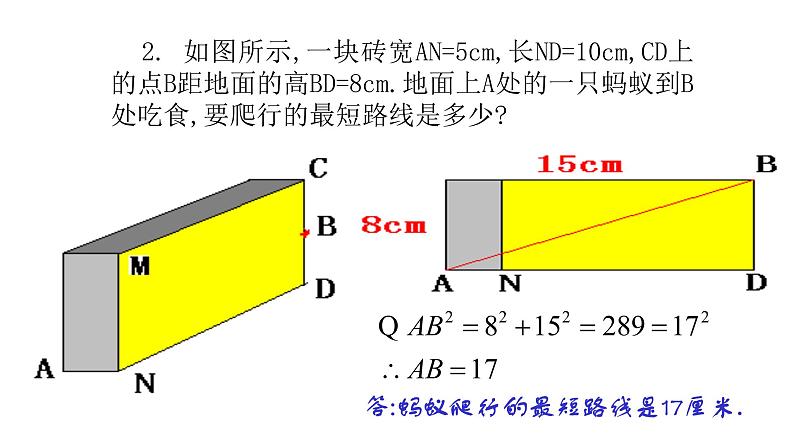
2. 如图所示,一块砖宽AN=5cm,长ND=10cm,CD上的点B距地面的高BD=8cm.地面上A处的一只蚂蚁到B处吃食,要爬行的最短路线是多少?
答:蚂蚁爬行的最短路线是17厘米.
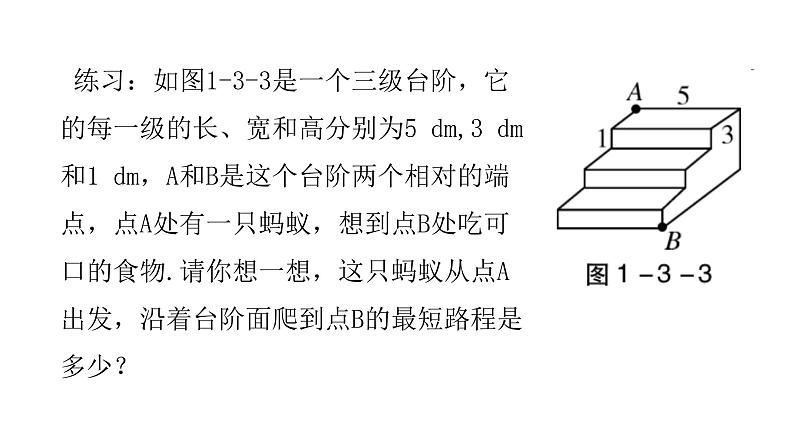
练习：如图1-3-3是一个三级台阶，它的每一级的长、宽和高分别为5 dm,3 dm和1 dm，A和B是这个台阶两个相对的端点，点A处有一只蚂蚁，想到点B处吃可口的食物.请你想一想，这只蚂蚁从点A出发，沿着台阶面爬到点B的最短路程是多少？
解：如答图1-3-1,将台阶展开成平面图形后，可知AC＝5 dm，BC＝3×(3＋1)＝12(dm)，∠C＝90°.在Rt△ABC中，因为AB2＝AC2＋BC2，所以AB2＝52＋122＝132.所以AB＝13（dm）.答：这只蚂蚁从点A出发,沿着台阶面爬到点B的最短路程是13 dm.
李叔叔想要检测雕塑底座正面的AD边和BC边是否分别垂直于底边AB，但他随身只带了卷尺，（1）你能替他想办法完成任务吗？
连接对角线AC，只要分别量出AB、BC、AC的长度即可。
若：AB2+BC2=AC2
则△ABC为直角三角形
同理可判断△ABD是否为直角三角形
（2）李叔叔量得AD长是30 cm，AB长是40 cm，BD长是50 cm，AD边垂直于AB边吗？为什么？
经计算AD2+AB2=BD2
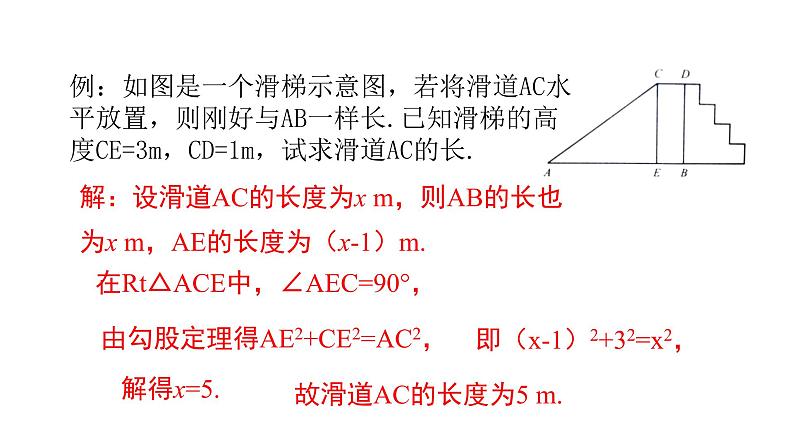
例：如图是一个滑梯示意图，若将滑道AC水平放置，则刚好与AB一样长.已知滑梯的高度CE=3m，CD=1m，试求滑道AC的长.
解：设滑道AC的长度为x m，则AB的长也为x m，AE的长度为（x-1）m.
在Rt△ACE中，∠AEC=90°，
由勾股定理得AE2+CE2=AC2，
即（x-1）2+32=x2，
故滑道AC的长度为5 m.
【例2】如图1-3-5，在一条东西走向河的一侧有一村庄C，河边原有两个取水点A，B，其中AB=AC，由于某种原因，由C到A的路现在已经不通，某村为方便村民取水决定在河边新建一个取水点H（A，H，B在一条直线上），并新修一条路CH，测得CB=3 km，CH=2.4 km，HB=1.8 km. （1）问CH是否为从村庄C到河边的最近路？（即问CH与AB是否垂直？）请通过计算加以说明；（2）求原来的路线AC的长.
解：（1）是.理由如下.在△CHB中，因为CH2+BH2=（2.4）2+（1.8）2=9, BC2=9,所以CH2+BH2=BC2.所以CH⊥AB.所以CH是从村庄C到河边的最近路.（2）设AC=x.在Rt△ACH中，由已知得AC=AB=x，AH=x-1.8，CH=2.4,由勾股定理,得AC2=AH2+CH2，所以x2=（x-1.8）2+（2.4）2.解得x=2.5.答：原来的路线AC的长为2.5 km.
练习： “中华人民共和国道路交通管理条例”规定：小汽车在城街路上行驶速度不得超过70 km/h，如图1-3-6，一辆小汽车在一条城市街道上直道行驶，某一时刻刚好行驶到路面对车速检测仪A的正前方60 m处的C点，过了5秒后，测得小汽车所在的B点与车速检测仪A之间的距离为100 m. （1）求B，C间的距离；（2）这辆小汽车超速了吗？请说明理由.
解：（1）在Rt△ABC中，因为AC=60 m，AB=100 m，且AB为斜边，根据勾股定理，得BC=80（m）.（2）这辆小汽车没有超速. 理由如下.因为80÷5=16（m/s），平均速度为16 m/s，16 m/s=57.6 km/h，57.6＜70，所以这辆小汽车没有超速.
习题1.4 1，2，3，4
1.如图1-3-8,长方形纸片ABCD沿对角线AC折叠,设点D落在D'处,BC 交AD'于点E,AB=6 cm,BC=8 cm,求阴影部分的面积.
解析　在△ABE和△CD'E中,∠B=∠D'=90°,∠AEB=∠CED',AB=CD',∴△ABE≌△CD'E,设AE=x cm(x>0),则BE=(8-x)cm.在Rt△ABE中,AB2+BE2=AE2,即62+(8-x)2=x2,∴x= ,∴EC=AE=  cm.
∴S阴影=0.5C·AB= × ×6= (cm2)
2.如图所示,将长方形纸片ABCD(四个角都是直角)折叠,使点D落在BC边上的点F处,已知AB=DC=8 cm,AD=BC=10 cm,求EC的长.
故EC的长为3 cm.
解析　设EC的长为x cm,则DE=(8-x)cm.
∵△ADE折叠后的图形是△AFE,
∴AD=AF,DE=EF=(8-x)cm.
∵AD=10 cm,∴AF=10 cm.
又∵AB=8 cm,AB2+BF2=AF2,
∴82+BF2=102,∴BF=6 cm.
∴FC=BC-BF=10-6=4(cm).
在Rt△EFC中,根据勾股定理,得FC2+EC2=EF2,
∴42+x2=(8-x)2,即16+x2=64-16x+x2,
化简,得16x=48,解得x=3.
3.如图,在B港有甲、乙两艘渔船同时 航行,若甲船沿北偏东60°方向以8海里/小时的速度前进,乙船沿南偏东 某方向以15海里/小时的速度前进,2小时后甲船到达M岛,乙船到达P岛, 两岛相距34海里,你知道乙船沿哪个方向航行吗?
解析　由题意知BM=8×2=16(海里),BP=15×2=30(海里),在△BMP中,BM2+BP2=256+900=1 156,PM2=342=1 156,∴△BMP是直角三角形,∠MBP=90°,∴∠ABP=180°-90°-60°=30°.故乙船沿南偏东30°方向航行.
4.我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图1-3-10所示,把枯木看作一个圆柱体,因一丈是十尺,所以该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛藤的最短长度是        尺.
解析　因为葛藤绕枯木五周而到达顶端,所以将枯木滚动5周,如图.由题意得AA'=15尺,A'B'=20尺,AB'的长就是葛藤的最短长度,∴AB'2=AA'2+A'B'2=152+202=625,∴AB'=25尺.
5.如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,∠BAC,∠ACB的平分线相交于点E,过点E作EF∥BC交AC于点F,求EF的长。
在Rt△EFN中,NF=CN-CF=8-2-CF=6-EF .
解如图,过点E分别作ED⊥AB,EM⊥BC,EN⊥AC,垂足分别为D,M,N,
∵∠BAC,∠ACB的平分线相交于点E,∴ED=EM=EN.
在Rt△ABC中,由勾股定理得AC=10.
设ED=EM=EN=x,易知AN=AD=6-x,CN=CM=8-x.
又6-x+8-x=10,∴x=2.
∴∠FEC=∠ECB,
∵∠FCE=∠ECB,
∴∠FEC=∠FCE.∴EF=CF.
∴EF2-(6-EF)2=22,解得x=
6.如图1 -3 -5,长方体的长为15cm, 宽为10cm,高为20cm,点B到点C的距离为5cm.一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是多少?
解:将长方体展开，分别得到如图①、图②、图③所示三种情况,连接AB.
在图①中,AB2 =AD2 + BD2 =202 + ( 10 +5)2 =625 ;
在图②中,AB2 =AE2 + BE2 = 102+ (20 +5)2 =725
在图③中,AB2 =AC2 + BC2 = (20 + 10)2 +52=925
∴最短距离AB =25cm.