初中1 菱形的性质与判定课文内容ppt课件

这是一份初中1 菱形的性质与判定课文内容ppt课件，共21页。PPT课件主要包含了情景导入，Sa+SbSc，a2+b2c2，勾2+股2弦2，课堂练习，美丽的勾股树，∴售货员没搞错，作业布置等内容，欢迎下载使用。

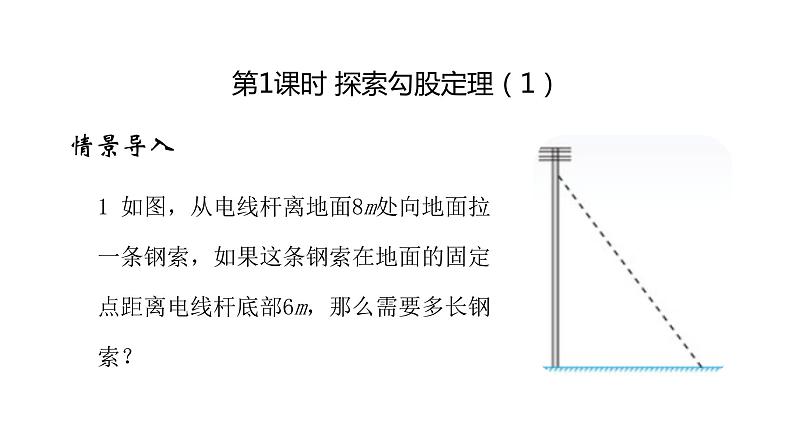
第1课时 探索勾股定理（1）
1 如图，从电线杆离地面8m处向地面拉一条钢索，如果这条钢索在地面的固定点距离电线杆底部6m，那么需要多长钢索？
(1)在纸上画若干个直角三角形，分别测量它们的三条边，看看三边长的平方之间有怎样的关系?与同伴进行交流.
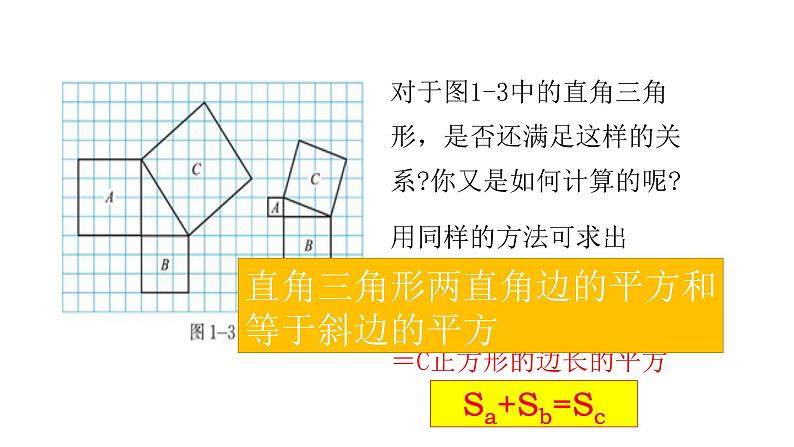
直角三角形两直角边的平方和等于斜边的平方
(2)如图1- 2,直角三角形三边的平方分别是多少，它们满足上面所猜想的数量关系吗?你是如何计算的?与同伴进行交流.
由图可知A正方形的边长的平方32=9， B正方形的边长的平方32=9SC=S大-(S1+S2+S3+S4)＝62-（0.5×3×3+0.5×3×3+0.5×3×3+0.5×3×3＝18故C正方形的面积是18，C正方形的边长的平方是18所以A正方形的边长的平方+B正方形的边长的平方＝C正方形的边长的平方
同样的方法求出第二个图
对于图1-3中的直角三角形，是否还满足这样的关系?你又是如何计算的呢?
用同样的方法可求出A正方形的边长的平方+B正方形的边长的平方＝C正方形的边长的平方
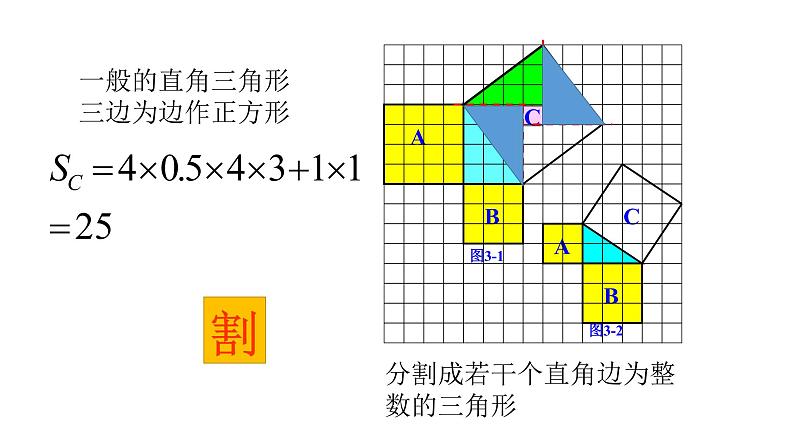
分割成若干个直角边为整数的三角形
一般的直角三角形三边为边作正方形
(3)如果直角三角形的两直角边分别为1.6 个单位长度和2.4个单位长度,上面所猜想的数量关系还成立吗?说明你的理由.
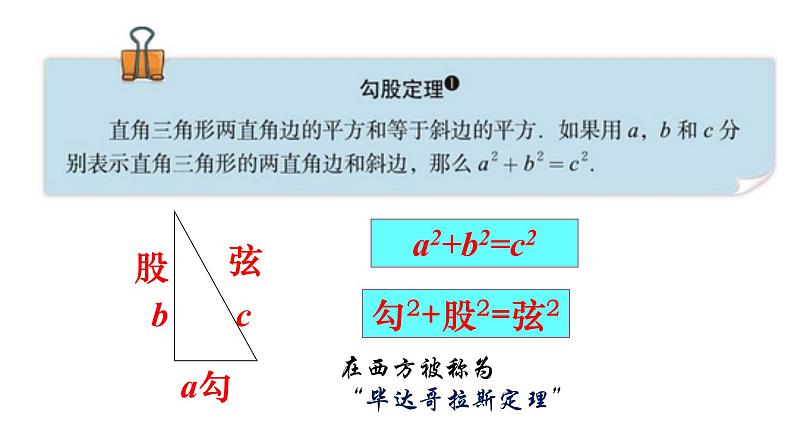
我国古代把直角三角形中较短的直角边称为勾，较长的直角边称为股，斜边称为弦。因此，我国称上面的结论为勾股定理.
发现:直角三角形两直角边的平方和等于斜边的平方
在西方被称为“毕达哥拉斯定理”
1 .求出下列三角形中未知边的长度.（1） （2）
解：（1）由勾股定理得： x2=62+82=100.
（2）由勾股定理得： y2=132－52=144.
常用的勾股数:3, 4, 5 5, 12, 137, 24, 25 15, 20, 25 9, 40, 41 11, 60, 61 8, 15, 17 12, 35, 37 20, 21, 29 10, 24, 26
它们的K倍也成立，如3K,4K.5K.
2.求出下列字母所代表的正方形的面积.
3.小明家买了一台29英寸的电视机.小明量了电视机的屏幕后，发现屏幕只有58厘米长和46厘米宽，他觉得一定是售货员搞错了.你能解释这是为什么吗？
29英寸×2.54=约74厘米
582+462=5480
荧屏对角线大约为74厘米
4.巩固练习.已知∠ACB=90°,CD⊥AB,AC=3,BC=4. 求CD的长.
2．在△ABC中，AB＝13，BC＝14.(1)如图①，AD⊥BC于点D，且BD＝5，则△ABC的面积为_______；(2)在(1)的条件下，如图②，点H是线段AC上任意一点，分别过点A，C作直线BH的垂线，垂足为E，F，设BH＝x，AE＝m，CF＝n，请用含x的代数式表示m＋n，并求m＋n的最大值和最小值．
1.如图1-1-4所示,已知Rt△ABC中,AB=4,分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值等于 (　　)
2.一直角三角形的三边长分别为2、3、x,那么以x为边长的正方形的面积为　　　    .
解析　以x为边长的正方形的面积为x2.当2和3都是直角边时,x2=4+9=13; 当3是斜边时,x2=9-4=5.故答案为13或5.