

还剩5页未读,
继续阅读
所属成套资源:2020新课标高考数学二轮精品教案
成套系列资料,整套一键下载
2020新课标高考数学二轮讲义:第三部分回顾6解析几何
展开
回顾6 解析几何
[必记知识]
1.直线方程的五种形式
(1)点斜式:y-y1=k(x-x1)(直线过点P1(x1,y1),且斜率为k,不包括y轴和平行于y轴的直线).
(2)斜截式:y=kx+b(b为直线l在y轴上的截距,且斜率为k,不包括y轴和平行于y轴的直线).
(3)两点式:=(直线过点P1(x1,y1),P2(x2,y2),且x1≠x2,y1≠y2,不包括坐标轴和平行于坐标轴的直线).
(4)截距式:+=1(a,b分别为直线的横、纵截距,且a≠0,b≠0,不包括坐标轴、平行于坐标轴和过原点的直线).
(5)一般式:Ax+By+C=0(其中A,B不同时为0).
2.直线的两种位置关系
当不重合的两条直线l1和l2的斜率存在时:
(1)两直线平行l1∥l2⇔k1=k2.
(2)两直线垂直l1⊥l2⇔k1·k2=-1.
[提醒] 当一条直线的斜率为0,另一条直线的斜率不存在时,两直线也垂直,此种情形易忽略.
3.三种距离公式
(1)A(x1,y1),B(x2,y2)两点间的距离
|AB|=.
(2)点到直线的距离d=(其中点P(x0,y0),直线方程为Ax+By+C=0).
(3)两平行线间的距离d=(其中两平行线方程分别为l1:Ax+By+C1=0,l1:Ax+By+C2=0且C1≠C2).
[提醒] 应用两平行线间距离公式时,注意两平行线方程中x,y的系数应对应相等.
4.圆的方程的两种形式
(1)圆的标准方程:(x-a)2+(y-b)2=r2.
(2)圆的一般方程:x2+y2+Dx+Ey+F=0(D2+E2-4F>0).
5.直线与圆、圆与圆的位置关系
(1)直线与圆的位置关系:相交、相切、相离,代数判断法与几何判断法.
(2)圆与圆的位置关系:相交、内切、外切、外离、内含,代数判断法与几何判断法.
6.椭圆的标准方程及几何性质
标准方程
+=1(a>b>0)
+=1(a>b>0)
几
何
性
质
图形
范围
-a≤x≤a,-b≤y≤b
-b≤x≤b,-a≤y≤a
对称性
对称轴:x轴,y轴;对称中心:原点
焦点
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
顶点
A1(-a,0),A2(a,0);
B1(0,-b),B2(0,b)
A1(0,-a),A2(0,a);
B1(-b,0),B2(b,0)
轴
线段A1A2,B1B2分别是椭圆的长轴和短轴;长轴长为2a,短轴长为2b
焦距
|F1F2|=2c
离心率
焦距与长轴长的比值:e∈(0,1)
a,b,c的关系
c2=a2-b2
[提醒] 椭圆的离心率反映了焦点远离中心的程度,e的大小决定了椭圆的形状,反映了椭圆的圆扁程度.因为a2=b2+c2,所以=,因此,当e越趋近于1时,越趋近于0,椭圆越扁;当e越趋近于0时,越趋近于1,椭圆越接近于圆.所以e越大椭圆越扁;e越小椭圆越圆,当且仅当a=b,c=0时,椭圆变为圆,方程为x2+y2=a2(a>0).
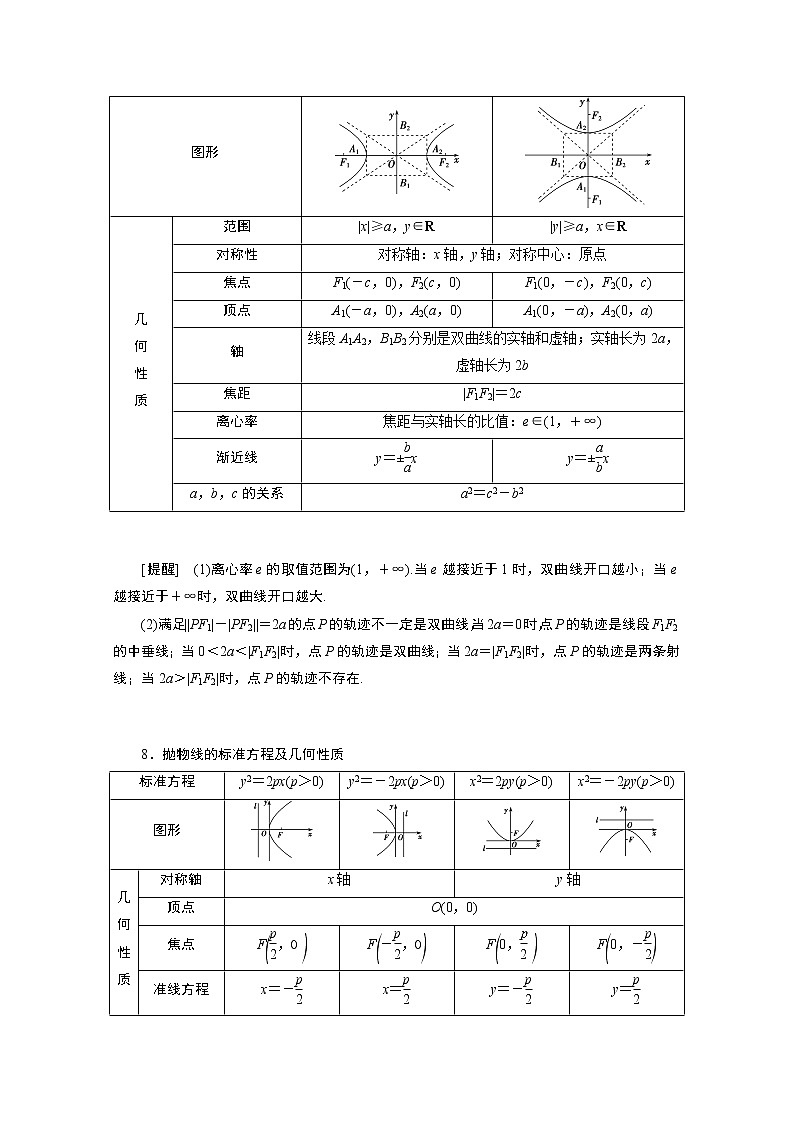
7.双曲线的标准方程及几何性质
标准方程
-=1
(a>0,b>0)
-=1
(a>0,b>0)
图形
几
何
性
质
范围
|x|≥a,y∈R
|y|≥a,x∈R
对称性
对称轴:x轴,y轴;对称中心:原点
焦点
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
顶点
A1(-a,0),A2(a,0)
A1(0,-a),A2(0,a)
轴
线段A1A2,B1B2分别是双曲线的实轴和虚轴;实轴长为2a,虚轴长为2b
焦距
|F1F2|=2c
离心率
焦距与实轴长的比值:e∈(1,+∞)
渐近线
y=±x
y=±x
a,b,c的关系
a2=c2-b2
[提醒] (1)离心率e的取值范围为(1,+∞).当e越接近于1时,双曲线开口越小;当e越接近于+∞时,双曲线开口越大.
(2)满足||PF1|-|PF2||=2a的点P的轨迹不一定是双曲线,当2a=0时,点P的轨迹是线段F1F2的中垂线;当0<2a<|F1F2|时,点P的轨迹是双曲线;当2a=|F1F2|时,点P的轨迹是两条射线;当2a>|F1F2|时,点P的轨迹不存在.
8.抛物线的标准方程及几何性质
标准方程
y2=2px(p>0)
y2=-2px(p>0)
x2=2py(p>0)
x2=-2py(p>0)
图形
几何性质
对称轴
x轴
y轴
顶点
O(0,0)
焦点
F
F
F
F
准线方程
x=-
x=
y=-
y=
范围
x≥0,y∈R
x≤0,y∈R
y≥0,x∈R
y≤0,x∈R
离心率
e=1
[必会结论]
1.与圆的切线有关的结论
(1)过圆x2+y2=r2上一点P(x0,y0)的切线方程为x0x+y0y=r2.
(2)过圆(x-a)2+(y-b)2=r2上一点P(x0,y0)的切线方程为(x0-a)(x-a)+(y0-b)(y-b)=r2.
(3)过圆x2+y2=r2外一点P(x0,y0)作圆的两条切线,切点为A,B,则过A,B两点的直线方程为x0x+y0y=r2.
(4)过圆x2+y2+Dx+Ey+F=0(D2+E2-4F>0)外一点P(x0,y0)引圆的切线,切点为T,则|PT|=.
(5)过圆C:(x-a)2+(y-b)2=r2(r>0)外一点P(x0,y0)作圆C的两条切线,切点分别为A,B,则切点弦AB所在的直线方程为(x0-a)(x-a)+(y0-b)(y-b)=r2.
(6)若圆的方程为(x-a)2+(y-b)2=r2(r>0),则过圆外一点P(x0,y0)的切线长d=.
2.椭圆中焦点三角形的相关结论
由椭圆上一点与两焦点所构成的三角形称为焦点三角形.解决焦点三角形问题常利用椭圆的定义和正、余弦定理.
以椭圆+=1(a>b>0)上一点P(x0,y0)(y0≠0)和焦点F1(-c,0),F2(c,0)为顶点的△PF1F2中,若∠F1PF2=θ,则
(1)|PF1|=a+ex0,|PF2|=a-ex0(焦半径公式),|PF1|+|PF2|=2a.(e为椭圆的离心率)
(2)4c2=|PF1|2+|PF2|2-2|PF1||PF2|·cos θ.
(3)S△PF1F2=|PF1||PF2|·sin θ=b2tan=c|y0|,当|y0|=b,即P为短轴端点时,S△PF1F2取得最大值,为bc.
(4)焦点三角形的周长为2(a+c).
3.双曲线的方程与渐近线方程的关系
(1)若双曲线的方程为-=1(a>0,b>0),则渐近线的方程为-=0,即y=±x.
(2)若渐近线的方程为y=±x(a>0,b>0),即±=0,则双曲线的方程可设为-=λ.
(3)若所求双曲线与双曲线-=1(a>0,b>0)有公共渐近线,其方程可设为-=λ(λ>0,焦点在x轴上;λ<0,焦点在y轴上).
4.双曲线常用的结论
(1)双曲线的焦点到其渐近线的距离为b.
(2)若P是双曲线右支上一点,F1,F2分别为双曲线的左、右焦点,则|PF1|min=a+c,|PF2|min=c-a.
(3)同支的焦点弦中最短的为通径(过焦点且垂直于长轴的弦),其长为,异支的弦中最短的为实轴,其长为2a.
(4)P是双曲线上不同于实轴两端点的任意一点,F1,F2分别为双曲线的左、右焦点,则kPA·kPB=,S△PF1F2=,其中θ为∠F1PF2.
(5)P是双曲线-=1(a>0,b>0)右支上不同于实轴端点的任意一点,F1,F2分别为双曲线的左、右焦点,I为△PF1F2内切圆的圆心,则圆心I的横坐标恒为a.
5.抛物线焦点弦的相关结论
设AB是过抛物线y2=2px(p>0)的焦点F的弦,若A(x1,y1),B(x2,y2),α为直线AB的倾斜角,则
(1)焦半径|AF|=x1+=,|BF|=x2+=.
(2)x1x2=,y1y2=-p2.
(3)弦长|AB|=x1+x2+p=.
(4)+=.
(5)以弦AB为直径的圆与准线相切.
(6)S△OAB=(O为抛物线的顶点).
[必练习题]
1.过圆x2+y2-x-y+=0的圆心,且倾斜角为的直线方程为( )
A.x-2y=0 B.x-2y+3=0
C.x-y=0 D.x-y+1=0
解析:选C.由题意知圆的圆心坐标为,所以过圆的圆心,且倾斜角为的直线方程为y=x,即x-y=0.
2.圆心为(4,0)且与直线x-y=0相切的圆的方程为( )
A.(x-4)2+y2=1 B.(x-4)2+y2=12
C.(x-4)2+y2=6 D.(x+4)2+y2=9
解析:选B.由题意,知圆的半径为圆心到直线x-y=0的距离,即r==2,结合圆心坐标可知,圆的方程为(x-4)2+y2=12,故选B.
3.若双曲线-=1(a>0,b>0)的离心率为,则其渐近方程为( )
A.y=±2x B.y=±4x
C.y=±x D.y=±x
解析:选C.由题意得e==,又a2+b2=c2,所以=,所以双曲线的渐近线方程为y=±x,选C.
4.设AB是椭圆的长轴,点C在椭圆上,且∠CBA=,若|AB|=4,|BC|=,则椭圆的两个焦点之间的距离为( )
A. B.
C. D.
解析:选A.不妨设椭圆的标准方程为+=1(a>b>0),如图,由题意知,2a=4,a=2,因为∠CBA=,|BC|=,所以点C的坐标为(-1,1),因为点C在椭圆上,所以+=1,所以b2=,所以c2=a2-b2=4-=,c=,则椭圆的两个焦点之间的距离为.
5.已知⊙M经过双曲线S:-=1的一个顶点和一个焦点,圆心M在双曲线S上,则圆心M到原点O的距离为( )
A.或 B.或
C. D.
解析:选D.因为⊙M经过双曲线S:-=1的一个顶点和一个焦点,圆心M在双曲线S上,所以⊙M不可能过异侧的顶点和焦点,不妨设⊙M经过双曲线的右顶点和右焦点,则圆心M到双曲线的右焦点(5,0)与右顶点(3,0)的距离相等,所以xM=4,代入双曲线方程可得yM=± =±,所以|OM|==,故选D.
6.设F为抛物线C:y2=3x的焦点,过F且倾斜角为30°的直线交C于A,B两点,O为坐标原点,则△OAB的面积为( )
A. B.
C. D.
解析:选D.易知直线AB的方程为y=,与y2=3x联立并消去x得4y2-12y-9=0.设A(x1,y1),B(x2,y2),则y1+y2=3,y1y2=-,S△OAB=|OF|·|y1-y2|=×==.故选D.
7.已知双曲线-=1(a>0),以原点为圆心,双曲线的实半轴长为半径的圆与双曲线的两条渐近线相交于A,B,C,D四点,四边形ABCD的面积为4,则双曲线的方程为( )
A.-=1 B.-=1
C.-=1 D.-=1
解析:选D.根据对称性,不妨设点A在第一象限,A(x,y),则解得因为四边形ABCD 的面积为4,所以4xy==4,解得a=2,故双曲线的方程为-=1,选D.
8.已知圆C1:(x-1)2+y2=2与圆C2:x2+(y-b)2=2(b>0)相交于A,B两点,且|AB|=2,则b=________.
解析:由题意知C1(1,0),C2(0,b),半径r1=r2=,所以线段AB和线段C1C2相互垂直平分,则|C1C2|=2,即1+b2=4,又b>0,故b=.
答案:
9.已知椭圆+=1(a>b>0),以原点O为圆心,短半轴长为半径作圆O,过椭圆的长轴的一端点P作圆O的两条切线,切点为A,B,若四边形PAOB为正方形,则椭圆的离心率为________.
解析:如图,因为四边形PAOB为正方形,且PA,PB为圆O的切线,所以△OAP是等腰直角三角形,故a=b,所以e==.
答案:
10.已知抛物线C1:y=x2(p>0)的焦点与双曲线C2:-y2=1的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p=________.
解析:由题意知,经过第一象限的双曲线的渐近线方程为y=x.抛物线的焦点为F1,双曲线的右焦点为F2(2,0).又y′=x,故抛物线C1在点M处的切线的斜率为,即x0=,所以x0=p,又点F1,F2(2,0),M三点共线,所以=,即p=.
答案:
回顾6 解析几何
[必记知识]
1.直线方程的五种形式
(1)点斜式:y-y1=k(x-x1)(直线过点P1(x1,y1),且斜率为k,不包括y轴和平行于y轴的直线).
(2)斜截式:y=kx+b(b为直线l在y轴上的截距,且斜率为k,不包括y轴和平行于y轴的直线).
(3)两点式:=(直线过点P1(x1,y1),P2(x2,y2),且x1≠x2,y1≠y2,不包括坐标轴和平行于坐标轴的直线).
(4)截距式:+=1(a,b分别为直线的横、纵截距,且a≠0,b≠0,不包括坐标轴、平行于坐标轴和过原点的直线).
(5)一般式:Ax+By+C=0(其中A,B不同时为0).
2.直线的两种位置关系
当不重合的两条直线l1和l2的斜率存在时:
(1)两直线平行l1∥l2⇔k1=k2.
(2)两直线垂直l1⊥l2⇔k1·k2=-1.
[提醒] 当一条直线的斜率为0,另一条直线的斜率不存在时,两直线也垂直,此种情形易忽略.
3.三种距离公式
(1)A(x1,y1),B(x2,y2)两点间的距离
|AB|=.
(2)点到直线的距离d=(其中点P(x0,y0),直线方程为Ax+By+C=0).
(3)两平行线间的距离d=(其中两平行线方程分别为l1:Ax+By+C1=0,l1:Ax+By+C2=0且C1≠C2).
[提醒] 应用两平行线间距离公式时,注意两平行线方程中x,y的系数应对应相等.
4.圆的方程的两种形式
(1)圆的标准方程:(x-a)2+(y-b)2=r2.
(2)圆的一般方程:x2+y2+Dx+Ey+F=0(D2+E2-4F>0).
5.直线与圆、圆与圆的位置关系
(1)直线与圆的位置关系:相交、相切、相离,代数判断法与几何判断法.
(2)圆与圆的位置关系:相交、内切、外切、外离、内含,代数判断法与几何判断法.
6.椭圆的标准方程及几何性质
标准方程
+=1(a>b>0)
+=1(a>b>0)
几
何
性
质
图形
范围
-a≤x≤a,-b≤y≤b
-b≤x≤b,-a≤y≤a
对称性
对称轴:x轴,y轴;对称中心:原点
焦点
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
顶点
A1(-a,0),A2(a,0);
B1(0,-b),B2(0,b)
A1(0,-a),A2(0,a);
B1(-b,0),B2(b,0)
轴
线段A1A2,B1B2分别是椭圆的长轴和短轴;长轴长为2a,短轴长为2b
焦距
|F1F2|=2c
离心率
焦距与长轴长的比值:e∈(0,1)
a,b,c的关系
c2=a2-b2
[提醒] 椭圆的离心率反映了焦点远离中心的程度,e的大小决定了椭圆的形状,反映了椭圆的圆扁程度.因为a2=b2+c2,所以=,因此,当e越趋近于1时,越趋近于0,椭圆越扁;当e越趋近于0时,越趋近于1,椭圆越接近于圆.所以e越大椭圆越扁;e越小椭圆越圆,当且仅当a=b,c=0时,椭圆变为圆,方程为x2+y2=a2(a>0).
7.双曲线的标准方程及几何性质
标准方程
-=1
(a>0,b>0)
-=1
(a>0,b>0)
图形
几
何
性
质
范围
|x|≥a,y∈R
|y|≥a,x∈R
对称性
对称轴:x轴,y轴;对称中心:原点
焦点
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
顶点
A1(-a,0),A2(a,0)
A1(0,-a),A2(0,a)
轴
线段A1A2,B1B2分别是双曲线的实轴和虚轴;实轴长为2a,虚轴长为2b
焦距
|F1F2|=2c
离心率
焦距与实轴长的比值:e∈(1,+∞)
渐近线
y=±x
y=±x
a,b,c的关系
a2=c2-b2
[提醒] (1)离心率e的取值范围为(1,+∞).当e越接近于1时,双曲线开口越小;当e越接近于+∞时,双曲线开口越大.
(2)满足||PF1|-|PF2||=2a的点P的轨迹不一定是双曲线,当2a=0时,点P的轨迹是线段F1F2的中垂线;当0<2a<|F1F2|时,点P的轨迹是双曲线;当2a=|F1F2|时,点P的轨迹是两条射线;当2a>|F1F2|时,点P的轨迹不存在.
8.抛物线的标准方程及几何性质
标准方程
y2=2px(p>0)
y2=-2px(p>0)
x2=2py(p>0)
x2=-2py(p>0)
图形
几何性质
对称轴
x轴
y轴
顶点
O(0,0)
焦点
F
F
F
F
准线方程
x=-
x=
y=-
y=
范围
x≥0,y∈R
x≤0,y∈R
y≥0,x∈R
y≤0,x∈R
离心率
e=1
[必会结论]
1.与圆的切线有关的结论
(1)过圆x2+y2=r2上一点P(x0,y0)的切线方程为x0x+y0y=r2.
(2)过圆(x-a)2+(y-b)2=r2上一点P(x0,y0)的切线方程为(x0-a)(x-a)+(y0-b)(y-b)=r2.
(3)过圆x2+y2=r2外一点P(x0,y0)作圆的两条切线,切点为A,B,则过A,B两点的直线方程为x0x+y0y=r2.
(4)过圆x2+y2+Dx+Ey+F=0(D2+E2-4F>0)外一点P(x0,y0)引圆的切线,切点为T,则|PT|=.
(5)过圆C:(x-a)2+(y-b)2=r2(r>0)外一点P(x0,y0)作圆C的两条切线,切点分别为A,B,则切点弦AB所在的直线方程为(x0-a)(x-a)+(y0-b)(y-b)=r2.
(6)若圆的方程为(x-a)2+(y-b)2=r2(r>0),则过圆外一点P(x0,y0)的切线长d=.
2.椭圆中焦点三角形的相关结论
由椭圆上一点与两焦点所构成的三角形称为焦点三角形.解决焦点三角形问题常利用椭圆的定义和正、余弦定理.
以椭圆+=1(a>b>0)上一点P(x0,y0)(y0≠0)和焦点F1(-c,0),F2(c,0)为顶点的△PF1F2中,若∠F1PF2=θ,则
(1)|PF1|=a+ex0,|PF2|=a-ex0(焦半径公式),|PF1|+|PF2|=2a.(e为椭圆的离心率)
(2)4c2=|PF1|2+|PF2|2-2|PF1||PF2|·cos θ.
(3)S△PF1F2=|PF1||PF2|·sin θ=b2tan=c|y0|,当|y0|=b,即P为短轴端点时,S△PF1F2取得最大值,为bc.
(4)焦点三角形的周长为2(a+c).
3.双曲线的方程与渐近线方程的关系
(1)若双曲线的方程为-=1(a>0,b>0),则渐近线的方程为-=0,即y=±x.
(2)若渐近线的方程为y=±x(a>0,b>0),即±=0,则双曲线的方程可设为-=λ.
(3)若所求双曲线与双曲线-=1(a>0,b>0)有公共渐近线,其方程可设为-=λ(λ>0,焦点在x轴上;λ<0,焦点在y轴上).
4.双曲线常用的结论
(1)双曲线的焦点到其渐近线的距离为b.
(2)若P是双曲线右支上一点,F1,F2分别为双曲线的左、右焦点,则|PF1|min=a+c,|PF2|min=c-a.
(3)同支的焦点弦中最短的为通径(过焦点且垂直于长轴的弦),其长为,异支的弦中最短的为实轴,其长为2a.
(4)P是双曲线上不同于实轴两端点的任意一点,F1,F2分别为双曲线的左、右焦点,则kPA·kPB=,S△PF1F2=,其中θ为∠F1PF2.
(5)P是双曲线-=1(a>0,b>0)右支上不同于实轴端点的任意一点,F1,F2分别为双曲线的左、右焦点,I为△PF1F2内切圆的圆心,则圆心I的横坐标恒为a.
5.抛物线焦点弦的相关结论
设AB是过抛物线y2=2px(p>0)的焦点F的弦,若A(x1,y1),B(x2,y2),α为直线AB的倾斜角,则
(1)焦半径|AF|=x1+=,|BF|=x2+=.
(2)x1x2=,y1y2=-p2.
(3)弦长|AB|=x1+x2+p=.
(4)+=.
(5)以弦AB为直径的圆与准线相切.
(6)S△OAB=(O为抛物线的顶点).
[必练习题]
1.过圆x2+y2-x-y+=0的圆心,且倾斜角为的直线方程为( )
A.x-2y=0 B.x-2y+3=0
C.x-y=0 D.x-y+1=0
解析:选C.由题意知圆的圆心坐标为,所以过圆的圆心,且倾斜角为的直线方程为y=x,即x-y=0.
2.圆心为(4,0)且与直线x-y=0相切的圆的方程为( )
A.(x-4)2+y2=1 B.(x-4)2+y2=12
C.(x-4)2+y2=6 D.(x+4)2+y2=9
解析:选B.由题意,知圆的半径为圆心到直线x-y=0的距离,即r==2,结合圆心坐标可知,圆的方程为(x-4)2+y2=12,故选B.
3.若双曲线-=1(a>0,b>0)的离心率为,则其渐近方程为( )
A.y=±2x B.y=±4x
C.y=±x D.y=±x
解析:选C.由题意得e==,又a2+b2=c2,所以=,所以双曲线的渐近线方程为y=±x,选C.
4.设AB是椭圆的长轴,点C在椭圆上,且∠CBA=,若|AB|=4,|BC|=,则椭圆的两个焦点之间的距离为( )
A. B.
C. D.
解析:选A.不妨设椭圆的标准方程为+=1(a>b>0),如图,由题意知,2a=4,a=2,因为∠CBA=,|BC|=,所以点C的坐标为(-1,1),因为点C在椭圆上,所以+=1,所以b2=,所以c2=a2-b2=4-=,c=,则椭圆的两个焦点之间的距离为.
5.已知⊙M经过双曲线S:-=1的一个顶点和一个焦点,圆心M在双曲线S上,则圆心M到原点O的距离为( )
A.或 B.或
C. D.
解析:选D.因为⊙M经过双曲线S:-=1的一个顶点和一个焦点,圆心M在双曲线S上,所以⊙M不可能过异侧的顶点和焦点,不妨设⊙M经过双曲线的右顶点和右焦点,则圆心M到双曲线的右焦点(5,0)与右顶点(3,0)的距离相等,所以xM=4,代入双曲线方程可得yM=± =±,所以|OM|==,故选D.
6.设F为抛物线C:y2=3x的焦点,过F且倾斜角为30°的直线交C于A,B两点,O为坐标原点,则△OAB的面积为( )
A. B.
C. D.
解析:选D.易知直线AB的方程为y=,与y2=3x联立并消去x得4y2-12y-9=0.设A(x1,y1),B(x2,y2),则y1+y2=3,y1y2=-,S△OAB=|OF|·|y1-y2|=×==.故选D.
7.已知双曲线-=1(a>0),以原点为圆心,双曲线的实半轴长为半径的圆与双曲线的两条渐近线相交于A,B,C,D四点,四边形ABCD的面积为4,则双曲线的方程为( )
A.-=1 B.-=1
C.-=1 D.-=1
解析:选D.根据对称性,不妨设点A在第一象限,A(x,y),则解得因为四边形ABCD 的面积为4,所以4xy==4,解得a=2,故双曲线的方程为-=1,选D.
8.已知圆C1:(x-1)2+y2=2与圆C2:x2+(y-b)2=2(b>0)相交于A,B两点,且|AB|=2,则b=________.
解析:由题意知C1(1,0),C2(0,b),半径r1=r2=,所以线段AB和线段C1C2相互垂直平分,则|C1C2|=2,即1+b2=4,又b>0,故b=.
答案:
9.已知椭圆+=1(a>b>0),以原点O为圆心,短半轴长为半径作圆O,过椭圆的长轴的一端点P作圆O的两条切线,切点为A,B,若四边形PAOB为正方形,则椭圆的离心率为________.
解析:如图,因为四边形PAOB为正方形,且PA,PB为圆O的切线,所以△OAP是等腰直角三角形,故a=b,所以e==.
答案:
10.已知抛物线C1:y=x2(p>0)的焦点与双曲线C2:-y2=1的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p=________.
解析:由题意知,经过第一象限的双曲线的渐近线方程为y=x.抛物线的焦点为F1,双曲线的右焦点为F2(2,0).又y′=x,故抛物线C1在点M处的切线的斜率为,即x0=,所以x0=p,又点F1,F2(2,0),M三点共线,所以=,即p=.
答案:
相关资料
更多








