

2020江苏高考理科数学二轮讲义:专题一第3讲 基本初等函数、函数与方程及函数应用
展开第3讲 基本初等函数、函数与方程及函数应用
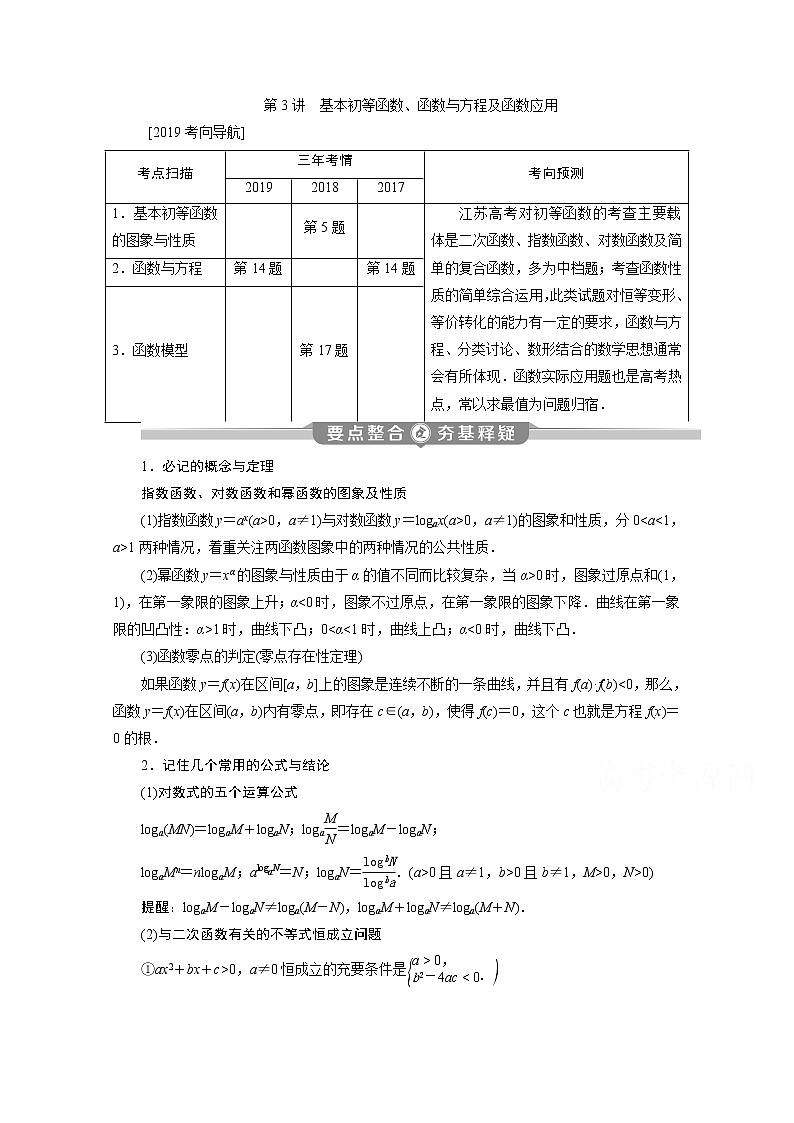
[2019考向导航]
考点扫描 | 三年考情 | 考向预测 | ||
2019 | 2018 | 2017 | ||
1.基本初等函数的图象与性质 |
| 第5题 |
| 江苏高考对初等函数的考查主要载体是二次函数、指数函数、对数函数及简单的复合函数,多为中档题;考查函数性质的简单综合运用,此类试题对恒等变形、等价转化的能力有一定的要求,函数与方程、分类讨论、数形结合的数学思想通常会有所体现.函数实际应用题也是高考热点,常以求最值为问题归宿. |
2.函数与方程 | 第14题 |
| 第14题 | |
3.函数模型 |
| 第17题 |
| |
1.必记的概念与定理
指数函数、对数函数和幂函数的图象及性质
(1)指数函数y=ax(a>0,a≠1)与对数函数y=logax(a>0,a≠1)的图象和性质,分0<a<1,a>1两种情况,着重关注两函数图象中的两种情况的公共性质.
(2)幂函数y=xα的图象与性质由于α的值不同而比较复杂,当α>0时,图象过原点和(1,1),在第一象限的图象上升;α<0时,图象不过原点,在第一象限的图象下降.曲线在第一象限的凹凸性:α>1时,曲线下凸;0<α<1时,曲线上凸;α<0时,曲线下凸.
(3)函数零点的判定(零点存在性定理)
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
2.记住几个常用的公式与结论
(1)对数式的五个运算公式
loga(MN)=logaM+logaN;loga=logaM-logaN;
logaMn=nlogaM;alogaN=N;logaN=.(a>0且a≠1,b>0且b≠1,M>0,N>0)
提醒:logaM-logaN≠loga(M-N),logaM+logaN≠loga(M+N).
(2)与二次函数有关的不等式恒成立问题
①ax2+bx+c>0,a≠0恒成立的充要条件是
②ax2+bx+c<0,a≠0恒成立的充要条件是
3.需要关注的易错易混点
(1)在比较幂值的大小时,必须结合幂值的特点,选择适当的函数.借助其单调性进行比较,准确掌握各个幂函数的图象和性质是解题的关键.
(2)解函数应用题常见的错误:①不会将实际问题抽象转化为函数模型或转化不全面;②在求解过程中忽视实际问题对变量参数的限制条件.
基本初等函数的图象与性质
[典型例题]
(1)已知a>b>1.若logab+logba=,ab=ba,则a=________,b=________.
(2)已知a>0,b>0,ab=8,则当a的值为________时,log2a·log2(2b)取得最大值.
【解析】 (1)由于a>b>1,则logab∈(0,1),因为logab+logba=,即logab+=,所以logab=或logab=2(舍去),所以a=b,即a=b2,所以ab=(b2)b=b2b=ba,所以a=2b,b2=2b,所以b=2(b=0舍去),a=4.
(2)由于a>0,b>0,ab=8,所以b=.
所以log2a·log2(2b)=log2a·log2=log2a·(4-log2a)=-(log2a-2)2+4,
当且仅当log2a=2,即a=4时,log2a·log2(2b)取得最大值4.
【答案】 (1)4 2 (2)4
指数函数、对数函数的图象和性质受底数a的影响,解决与指数、对数函数特别是与单调性有关的问题时,首先要看底数a的范围.
[对点训练]
1.(2019·南通市高三模拟)已知函数f(x)=loga(x+b)(a>0且a≠1,b∈R)的图象如图所示,则a+b的值是________.
[解析] 将(-3,0),(0,-2)分别代入解析式得loga(-3+b)=0,logab=-2,解得a=,b=4,从而a+b=.
[答案]
2.使log2(-x)<x+1成立的x的取值范围是________.
[解析] 作出函数y=log2(-x)及y=x+1的图象.其中y=log2(-x)及y=log2x的图象关于y轴对称,观察图象(如图所示)知,-1<x<0,
即x∈(-1,0).也可把原不等式化为后作图.
[答案] (-1,0)
函数与方程
[典型例题]
(1)设函数f(x)的定义域为R,f(-x)=f(x),f(x)=f(2-x),当x∈[0,1]时,f(x)=x3,则函数g(x)=|cos πx|-f(x)在区间上零点的个数为__________________________.
(2)(2019·高考江苏卷)设f(x),g(x)是定义在R上的两个周期函数,f(x)的周期为4,g(x)的周期为2,且f(x)是奇函数.当x∈(0,2]时,f(x)=,g(x)=其中k>0.若在区间(0,9]上,关于x的方程f(x)=g(x)有8个不同的实数根,则k的取值范围是________.
【解析】 (1)由f(-x)=f(x),得f(x)的图象关于y轴对称.由f(x)=f(2-x),得f(x)的图象关于直线x=1对称.当x∈[0,1]时,f(x)=x3,所以f(x)在[-1,2]上的图象如图.
令g(x)=|cos πx|-f(x)=0,得|cos πx|=f(x),两函数y=f(x)与y=|cos πx|的图象在上的交点有5个.
(2)当x∈(0,2]时,令y=,则(x-1)2+y2=1,y≥0,即f(x)的图象是以(1,0)为圆心、1为半径的半圆,利用f(x)是奇函数,且周期为4,画出函数f(x)在(0,9]上的图象,再在同一坐标系中作出函数g(x)(x∈(0,9])的图象,如图,关于x的方程f(x)=g(x)在(0,9]上有8个不同的实数根,即两个函数的图象有8个不同的交点,数形结合知g(x)(x∈(0,1])与f(x)(x∈(0,1])的图象有2个不同的交点时满足题意,当直线y=k(x+2)经过点(1,1)时,k=,当直线y=k(x+2)与半圆(x-1)2+y2=1(y≥0)相切时,=1,k=或k=-(舍去),所以k的取值范围是.
【答案】 (1)5 (2)
判断函数零点个数的方法
(1)解方程法:若对应方程f(x)=0可解时,通过解方程,则有几个解就有几个零点.
(2)零点存在性定理法:利用定理不仅要判断函数在区间[a,b]上是连续不断的曲线,且f(a)·f(b)<0,还必须结合函数的图象与性质(如单调性、奇偶性、周期性、对称性)才能确定函数有多少个零点.
(3)数形结合法:转化为两个函数的图象的交点个数问题.先画出两个函数的图象,看其交点的个数,其中交点的个数,就是函数零点的个数.
[对点训练]
3.(2019·南京四校高三联考)已知周期为4的函数f(x)=,则方程3f(x)=x的根的个数为________.
[解析] 作出函数y=f(x)的图象及直线y=如图所示,则两个图象的交点个数为3,即方程的根的个数为3.
[答案] 3
4.(2019·苏州市高三调研)已知函数f(x)=ax+x-b的零点x0∈(n,n+1)(n∈Z),其中常数a、b满足2a=3,3b=2,则n=________.
[解析] f(x)=ax+x-b的零点x0就是方程ax=-x+b的根.设y1=ax,y2=-x+b,
故x0就是两函数交点的横坐标,
由2a=3,3b=2,得a>1,0<b<1.可知f(x)为增函数.
当x=-1时,y1==log32<y2=1+b=1+log32,
当x=0时,y1=a0=1>y2=b,
所以-1<x0<0,所以n=-1.
[答案] -1
函数模型
[典型例题]
(2018·高考江苏卷)某农场有一块农田,如图所示,它的边界由圆O的一段圆弧MPN(P为此圆弧的中点)和线段MN构成.已知圆O的半径为40米,点P到MN的距离为50米.现规划在此农田上修建两个温室大棚,大棚Ⅰ内的地块形状为矩形ABCD,大棚Ⅱ内的地块形状为△CDP,要求A,B均在线段MN上,C,D均在圆弧上.设OC与MN所成的角为θ.
(1)用θ分别表示矩形ABCD和△CDP的面积,并确定sin θ的取值范围;
(2)若大棚Ⅰ内种植甲种蔬菜,大棚Ⅱ内种植乙种蔬菜,且甲、乙两种蔬菜的单位面积年产值之比为4∶3.求当θ为何值时,能使甲、乙两种蔬菜的年总产值最大.
【解】 (1)设PO的延长线交MN于H,则PH⊥MN,所以OH=10.
过O作OE⊥BC于E,则OE∥MN,所以∠COE=θ,
故OE=40cos θ,
EC=40sin θ,
则矩形ABCD的面积为2×40cos θ·(40sin θ+10)=800(4sin θcos θ+cos θ),△CDP的面积为
×2×40cos θ(40-40sin θ)=1 600(cos θ-sin θcos θ).
过N作GN⊥MN,分别交圆弧和OE的延长线于G和K,则GK=KN=10.连结OG,令∠GOK=θ0,则sin θ0=,θ0∈.
当θ∈时,才能作出满足条件的矩形ABCD,
所以sin θ的取值范围是.
(2)因为甲、乙两种蔬菜的单位面积年产值之比为4∶3,
设甲的单位面积的年产值为4k,乙的单位面积的年产值为3k(k>0),则年总产值为4k×800(4sin θcos θ+cos θ)+3k×1 600(cos θ-sin θcos θ)=8 000k(sin θcos θ+cos θ),θ∈.
设f(θ)=sin θcos θ+cos θ,θ∈,则
f′(θ)=cos2θ-sin2θ-sin θ=-(2sin2θ+sin θ-1)=-(2sin θ-1)·(sin θ+1).
令f′(θ)=0,得θ=,
当θ∈时,f′(θ)>0,所以f(θ)为增函数;
当θ∈时,f′(θ)<0,所以f(θ)为减函数,
因此,当θ=时,f(θ)取到最大值.
应用函数模型解决实际问题的一般程序是:
⇒⇒⇒
与函数有关的应用题,经常涉及物价、路程、产值、环保等实际问题,也可涉及角度、面积、体积、造价的最优化问题.解答这类问题的关键是建立相关函数解析式,然后应用函数、方程、不等式和导数的有关知识加以综合解答.
[对点训练]
5.(2019·江苏省四星级学校联考)某品牌开发了一种新产品,欲在沿海城市寻找一个工厂代理加工生产该新产品,由于该新产品的专利保护要求比较高,某种核心配件只能从总公司购买并且由总公司统一配送,该厂每天需要此核心配件200个,配件的价格为1.8元/个,每次购买配件需支付运费236元.每次购买来的配件还需支付保密费用(若n天购买一次,则需要支付n天的保密费用),其标准如下:7天以内(含7天),均按10元/天支付;7天以外,根据当天还未生产时剩余配件的数量,以每天0.03元/个支付.
(1)当9天购买一次配件时,求该厂用于配件的保密费用p(元)的值;
(2)设该厂x天购买一次配件,求该厂在这x天中用于配件的总费用y(元)关于x的函数关系式,并求该厂多少天购买一次配件才能使平均每天支付的费用最少.
[解] (1)当9天购买一次配件时,该厂用于配件的保密费用p=70+0.03×200×(2+1)=88(元).
(2)①当0<x≤7时,y=1.8×200x+10x+236=370x+236.
②当x>7时,y=1.8×200x+236+70+200×0.03×[(x-7)+(x-8)+…+2+1]=3x2+321x+432,
所以y=.
设该厂x天购买一次配件时,平均每天支付的费用为f(x)元,
则f(x)=.
当0<x≤7时,f(x)=370+,f(x)是(0,7]上的减函数,
所以当x=7时,f(x)有最小值.
当x>7时,f(x)=3x++321=3+321≥3×2×+321=393,
当且仅当x=,即x=12时取等号.
又>393,所以当该厂12天购买一次配件时才能使平均每天支付的费用最少.
1.已知点M在幂函数f(x)的图象上,则f(x)的表达式为________.
[解析] 设幂函数的解析式为f(x)=xα,则3=,得
α=-2.故f(x)=x-2.
[答案] f(x)=x-2
2.(2019·常州模拟) 函数y=的值域为________.
[解析] 由指数函数性质知值域为(0,+∞).
[答案] (0,+∞)
3.函数y=|x|2-|x|-12两个零点的差的绝对值是________.
[解析] 令|x|2-|x|-12=0,得(|x|-4)(|x|+3)=0,
即|x|=4,
所以两个零点的差的绝对值是|4-(-4)|=8.
[答案] 8
4.(2019·绵阳期中)若a=30.6,b=log30.2,c=0.63,则a,b,c的大小关系为________.
[解析] 30.6>1,log30.2<0,0<0.63<1,所以a>c>b.
[答案] a>c>b
5.(2019·山西大学附中期中)有四个函数:①y=x;②y=21-x;③y=ln(x+1);④y=|1-x|.其中在区间(0,1)内单调递减的函数的序号是________.
[解析] 分析题意可知①③显然不满足题意,画出②④中的函数图象(图略),易知②④中的函数满足在(0,1)内单调递减.
[答案] ②④
6.设2a=5b=m,且+=2,则m=________.
[解析] 因为2a=5b=m,所以a=log2m,b=log5m,
所以+=+=logm2+logm5=logm10=2.所以m=.
[答案]
7.(2019·南京、盐城高三模拟)已知函数f(x)=-kx(e为自然对数的底数)有且只有一个零点,则实数k的取值范围是________.
[解析] 由题意,知x≠0,函数f(x)有且只有一个零点等价于方程-kx=0只有一个根,即方程=k只有一个根,设g(x)=,则函数g(x)=的图象与直线y=k只有一个交点.
因为g′(x)=,所以函数g(x)在(-∞,0)上为增函数,在(0,2)上为减函数,在(2,+∞)上为增函数,g(x)的极小值g(2)=,且x→0时,g(x)→+∞,x→-∞时,g(x)→0,x→+∞时,g(x)→+∞,则g(x)的图象如图所示,由图易知0<k<.
[答案]
8.(2019·高三第二次调研测试)定义在R上的奇函数f(x)满足f(x+4)=f(x),且在[2,4)上,f(x)=则函数y=f(x) -log5|x|的零点个数为______.
[解析] 由f(x+4)=f(x)得奇函数f(x)的最小正周期为4,作出函数f(x)与y=log5|x|的部分图象如图所示,根据图象易知,函数y=f(x)与y=log5|x|的图象有5个交点,故函数y=f(x)-log5|x|的零点个数是5.
[答案] 5
9.设a>0且a≠1,函数y=a2x+2ax-1在[-1,1]上的最大值是14,则a的值为________.
[解析] 令t=ax(a>0且a≠1),则原函数化为y=(t+1)2-2(t>0).
①当0<a<1时,x∈[-1,1],t=ax∈,
此时f(t)在上为增函数.
所以f(t)max=f=-2=14.
所以=16,所以a=-或a=.
又因为a>0,所以a=.
②当a>1时,x∈[-1,1],t=ax∈,
此时f(t)在上是增函数.
所以f(t)max=f(a)=(a+1)2-2=14,
解得a=3(a=-5舍去).
综上得a=或3.
[答案] 或3
10.(2019·江苏省高考名校联考信息卷(五))已知函数f(x)=(x∈R),g(x)满足g(2-x)+g(x)=0.若函数f(x-1)与函数g(x)的图象恰好有2 019个交点,则这2 019个交点的横坐标之和为______.
[解析] 由于f(-x)+f(x)=+=0,所以函数f(x)=为奇函数,从而函数f(x-1)的图象关于点(1,0)对称.由函数g(x)满足g(2-x)+g(x)=0,可知g(x)的图象也关于点(1,0)对称,所以函数F(x)=g(x)-f(x-1)的图象关于点(1,0)对称,从而这2 019个零点关于点(1,0)对称,由于F(1)=g(1)-f(0)=0,所以x=1是F(x)的一个零点,其余2 018个零点首尾结合,两两关于点(1,0)对称,和为2 018,故所有这些零点之和为2 019,即函数f(x-1)与函数g(x)的图象的2 019个交点的横坐标之和为2 019.
[答案] 2 019
11.已知函数f(x)=x2,g(x)=x-1.
(1)若存在x∈R使f(x)<b·g(x),求实数b的取值范围;
(2)设F(x)=f(x)-mg(x)+1-m-m2,且|F(x)|在[0,1]上单调递增,求实数m的取值范围.
[解] (1)∃x∈R,f(x)<bg(x)⇒∃x∈R,x2-bx+b<0⇒(-b)2-4b>0⇒b<0或b>4.
故b的取值范围为(-∞,0)∪(4,+∞).
(2)F(x)=x2-mx+1-m2,
Δ=m2-4(1-m2)=5m2-4.
①当Δ≤0,即-≤m≤时,
则必需⇒-≤m≤0.
②当Δ>0,即m<-或m>时,
设方程F(x)=0的根为x1,x2(x1<x2).
若≥1,则x1≤0,
即⇒m≥2;
若≤0,则x2≤0,
即⇒-1≤m<-.
综上所述,m的取值范围为[-1,0]∪[2,+∞).
12.(2019·南通市高三模拟)某宾馆在装修时,为了美观,欲将客房的窗户设计成半径为1 m的圆形,并用四根木条将圆分成9个区域,其中四边形ABCD为中心在圆心的矩形.现计划将矩形ABCD区域设计为可推拉的窗口.
(1)若窗口ABCD为正方形,且面积大于 m2(木条宽度忽略不计),求四根木条总长的取值范围;
(2)若四根木条总长为6 m,求窗口ABCD面积的最大值.
[解] (1)当ABCD为正方形时,四根木条的长度相等,设一根木条长为x m,
则正方形的边长为2= m.
因为S四边形ABCD>,所以4-x2>,即0<x<.
又四根木条将圆分成9个区域,所以x>,
所以4<4x<2,
即四根木条总长的取值范围为(4,2).
(2)设AB所在木条长为a m,BC所在木条长为b m.
由条件知,2a+2b=6,即a+b=3.
因为a,b∈(0,2),所以b=3-a∈(0,2),从而a,b∈(1,2).
由于AB=2,BC=2,
S矩形ABCD=4·=·,
因为·≤≤=,
当且仅当a=b=∈(1,2)时,S矩形ABCD=,
所以窗口ABCD面积的最大值为 m2.
13.(2019·江苏省高考名校联考(九))某公司研发了一款新型的洗衣液,其具有“强力去渍、快速去污”的效果.研发人员通过多次试验发现每投放a(1≤a≤4,a∈R)克洗衣液在一定量水的洗衣机中,它在水中释放的浓度y(克/升)随着时间x(分钟)变化的函数关系式近似为y=a·f(x),其中f(x)=且当水中洗衣液的浓度不低于16克/升时,才能够起到有效去污的作用.若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和.
(1)若一次投放4克的洗衣液,则有效去污时间可达几分钟?
(2)如果第一次投放4克洗衣液,4分钟后再投放4克洗衣液,写出第二次投放之后洗衣液在水中释放的浓度y(克/升)与时间x(分钟)的函数关系式,其中x表示第一次投放的时长,并判断接下来的4分钟是否能够持续有效去污.
[解] (1)当一次投放4克洗衣液,即a=4时,
y=4·f(x)=
因为当水中洗衣液的浓度不低于16克/升时,才能够起到有效去污的作用,所以当0≤x≤4时,由8x≥16,解得x≥2,所以此时2≤x≤4;当x>4时,由+8≥16,得x≤6,所以此时4<x≤6.
综上可得2≤x≤6.
所以若一次投放4克洗衣液,有效去污时间可达4分钟.
(2)由(1)得,当4≤x≤8时,
y=+8+8(x-4)=+8(x-3);
当x>8时,y=+8++8
=++16.
综上,y=
当4≤x≤8时,
y=+8(x-3)≥2=16,当且仅当x=3+时等号成立.
又16>16,所以接下来的4分钟能够有效去污.
14.设函数fn(x)=xn+bx+c(n∈N*,b,c∈R).
(1)设n≥2,b=1,c=-1,证明:fn(x)在区间内存在唯一零点;
(2)设n=2,若对任意x1,x2∈[-1,1],有|f2(x1)-f2(x2)|≤4,求b的取值范围.
[解] (1)证明:b=1,c=-1,n≥2时,fn(x)=xn+x-1.
因为fnfn(1)=×1<0,
所以fn(x)在内存在零点.
又当x∈时,f′n(x)=nxn-1+1>0,
所以fn(x)在上是单调递增的,
所以fn(x)在内存在唯一零点.
(2)当n=2时,f2(x)=x2+bx+c.
对任意x1,x2∈[-1,1]都有|f2(x1)-f2(x2)|≤4等价于f2(x)在[-1,1]上的最大值与最小值之差M≤4.
据此分类讨论如下:
①当>1,即|b|>2时,
M=|f2(1)-f2(-1)|=2|b|>4,与题设矛盾.
②当-1≤-<0,即0<b≤2时,
M=f2(1)-f2=≤4恒成立.
③当0≤-≤1,即-2≤b≤0时,
M=f2(-1)-f2=≤4恒成立.
综上可知,-2≤b≤2.








