2021版高考文科数学（北师大版）一轮复习教师用书：第四章　第6讲　第1课时　正弦定理和余弦定理

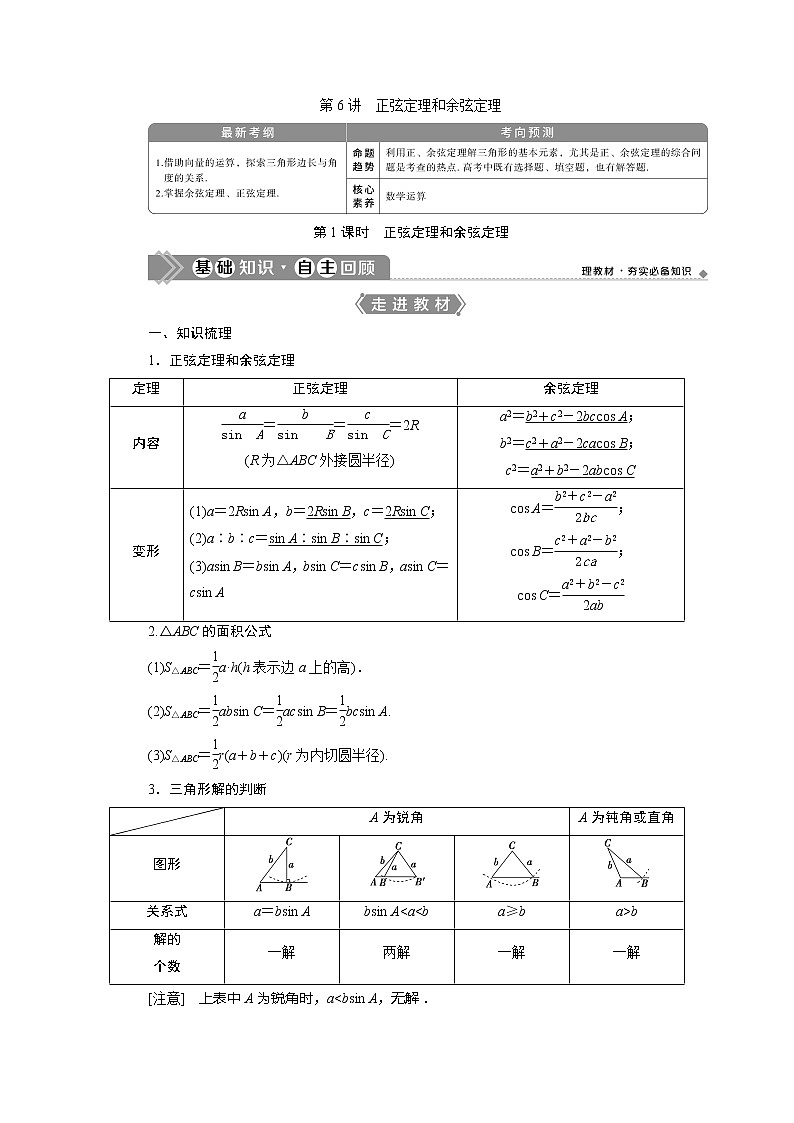
第6讲　正弦定理和余弦定理第1课时　正弦定理和余弦定理一、知识梳理1．正弦定理和余弦定理定理正弦定理余弦定理内容＝＝＝2R(R为△ABC外接圆半径)a2＝b2＋c2－2bccos A；b2＝c2＋a2－2cacos B；c2＝a2＋b2－2abcos C变形(1)a＝2Rsin A，b＝2Rsin B，c＝2Rsin C；(2)a∶b∶c＝sin A∶sin B∶sin C；(3)asin B＝bsin A，bsin C＝csin B，asin C＝csin Acos A＝；cos B＝；cos C＝2.△ABC的面积公式(1)S△ABC＝a·h(h表示边a上的高)．(2)S△ABC＝absin C＝acsin B＝bcsin A.(3)S△ABC＝r(a＋b＋c)(r为内切圆半径). 3．三角形解的判断 A为锐角A为钝角或直角图形关系式a＝bsin Absin A<a<ba≥ba>b解的个数一解两解一解一解[注意]　上表中A为锐角时，a<bsin A，无解．A为钝角或直角时，a＝b，a<b均无解．常用结论1．三角形内角和定理在△ABC中，A＋B＋C＝π；变形：＝－.2．三角形中的三角函数关系(1)sin(A＋B)＝sin C.(2)cos(A＋B)＝－cos C.(3)sin＝cos .(4)cos＝sin .3．三角形中的射影定理在△ABC中，a＝bcos C＋ccos B；b＝acos C＋ccos A；c＝bcos A＋acos B.二、教材衍化   1．在△ABC中，角A，B，C所对的边分别为a，b，c若c<bcos A，则△ABC为(　　)A．钝角三角形　　　　　 B．直角三角形C．锐角三角形  D．等边三角形答案：A2．在△ABC中，AB＝5，AC＝3，BC＝7，则∠BAC＝(　　)A.   B.C.  D．解析：选C.因为在△ABC中，设AB＝c＝5，AC＝b＝3，BC＝a＝7，所以由余弦定理得cos∠BAC＝＝＝－，因为∠BAC为△ABC的内角，所以∠BAC＝.故选C.3．在△ABC中，A＝60°，AC＝4，BC＝2，则△ABC的面积等于        ．解析：设△ABC中，角A，B，C对应的边分别为a，b，c，由题意及余弦定理得cos A＝＝＝，解得c＝2.所以S＝bcsin A＝×4×2×sin 60°＝2.答案：2一、思考辨析判断正误(正确的打“√”，错误的打“×”)(1)三角形中三边之比等于相应的三个内角之比．(　　)(2)在△ABC中，若sin A＞sin B，则A＞B.(　　)(3)在△ABC中的六个元素中，已知任意三个元素可求其他元素．(　　)答案：(1)×　(2)√　(3)×二、易错纠偏(1)利用正弦定理求角，忽视条件限制出现增根；(2)不会灵活运用正弦、余弦定理．1．△ABC的内角A，B，C的对边分别为a，b，c.已知C＝60°，b＝，c＝3，则A＝        ．解析：由题意：＝，即sin B＝＝＝，结合b＜c可得B＝45°，则A＝180°－B－C＝75°.答案：75°2．设△ABC的内角A，B，C的对边分别为a，b，c，且a＝2，cos C＝－，3sin A＝2sin B，则c＝        ．解析：由3sin A＝2sin B及正弦定理，得3a＝2b，所以b＝a＝3.由余弦定理cos C＝，得－＝，解得c＝4.答案：4　　　　利用正弦、余弦定理解三角形(师生共研) (1)(2019·高考全国卷Ⅰ)△ABC的内角A，B，C的对边分别为a，b，c.已知asin A－bsin B＝4csin C，cos A＝－，则＝(　　)A．6　　　　　　　　　　 B．5C．4  D．3(2)(2020·济南市学习质量评估)已知△ABC的内角A，B，C的对边分别为a，b，c，且2c＋a＝2bcos A.①求角B的大小；②若a＝5，c＝3，边AC的中点为D，求BD的长．【解】　(1)选A.由题意及正弦定理得，b2－a2＝－4c2，所以由余弦定理得，cos A＝＝＝－，得＝6.故选A.(2)①由2c＋a＝2bcos A及正弦定理，得2sin C＋sin A＝2sin Bcos A，又sin C＝sin(A＋B)＝sin Acos B＋cos Asin B，所以2sin Acos B＋sin A＝0，因为sin A≠0，所以cos B＝－，因为0＜B＜π，所以B＝.②由余弦定理得b2＝a2＋c2－2a·ccos∠ABC＝52＋32＋5×3＝49，所以b＝7，所以AD＝.因为cos∠BAC＝＝＝，所以BD2＝AB2＋AD2－2·AB·ADcos∠BAC＝9＋－2×3××＝，所以BD＝.(1)正、余弦定理的选用①利用正弦定理可解决两类三角形问题：一是已知两角和一角的对边，求其他边或角；二是已知两边和一边的对角，求其他边或角；②利用余弦定理可解决两类三角形问题：一是已知两边和它们的夹角，求其他边或角；二是已知三边求角．由于这两种情形下的三角形是唯一确定的，所以其解也是唯一的．(2)三角形解的个数的判断已知两角和一边，该三角形是确定的，其解是唯一的；已知两边和一边的对角，该三角形具有不唯一性，通常根据三角函数值的有界性和大边对大角定理进行判断．1．(一题多解)(2020·江西五市联考)在△ABC中，角A，B，C所对的边分别为a，b，c，已知a＝1，b＝，A＝30°，B为锐角，那么A∶B∶C为(　　)A．1∶1∶3  B．1∶2∶3C．1∶3∶2  D．1∶4∶1解析：选B.法一：由正弦定理＝，得sin B＝＝.因为B为锐角，所以B＝60°，则C＝90°，故A∶B∶C＝1∶2∶3，选B.法二：由a2＝b2＋c2－2bccos A，得c2－3c＋2＝0，解得c＝1或c＝2.当c＝1时，△ABC为等腰三角形，B＝120°，与已知矛盾，当c＝2时，a<b<c，则A<B<C，排除选项A，C，D，故选B.2．(2020·河南南阳四校联考)在△ABC中，角A，B，C的对边分别为a，b，c，若b＝8，c＝3，A＝60°，则此三角形外接圆的半径R＝(　　)A.   B.C.  D．解析：选D.因为b＝8，c＝3，A＝60°，所以a2＝b2＋c2－2bccos A＝64＋9－2×8×3×＝49，所以a＝7，所以此三角形外接圆的直径2R＝＝＝，所以R＝，故选D.3．(2019·高考全国卷Ⅰ改编)△ABC的内角A，B，C的对边分别为a，b，c，设(sin B－sin C)2＝sin2A－sin Bsin C.(1)求A；(2)若a＋b＝2c，求C.解：(1)由已知得sin2B＋sin2C－sin2A＝sin Bsin C，故由正弦定理得b2＋c2－a2＝bc.由余弦定理得cos A＝＝.因为0°＜A＜180°，所以A＝60°.(2)由(1)知B＝120°－C，由题设及正弦定理得sin A＋sin(120°－C)＝2sin C，即＋cos C＋sin C＝2sin C，可得cos(C＋60°)＝－.由于0°＜C＜120°，所以C＋60°＝135°，即C＝75°.　　　　　　判断三角形的形状(典例迁移) (1)(一题多解)设△ABC的内角A，B，C所对的边分别为a，b，c，若bcos C＋ccos B＝asin A，则△ABC的形状为(　　)A．直角三角形  B．锐角三角形C．钝角三角形  D．不确定(2)在△ABC中，若c－acos B＝(2a－b)cos A，则△ABC的形状为        ．【解析】　(1)法一：因为bcos C＋ccos B＝b·＋c·＝＝a，所以asin A＝a即sin A＝1，故A＝，因此△ABC是直角三角形．法二：因为bcos C＋ccos B＝asin A，所以sin Bcos C＋sin Ccos B＝sin2 A，即sin(B＋C)＝sin2 A，所以sin A＝sin2 A，故sin A＝1，即A＝，因此△ABC是直角三角形．(2)因为c－acos B＝(2a－b)cos A，所以由正弦定理得sin C－sin Acos B＝2sin Acos A－sin Bcos A，所以sin(A＋B)－sin Acos B＝2sin Acos A－sin Bcos A，故cos A(sin B－sin A)＝0，所以cos A＝0或sin A＝sin B，即A＝或A＝B，故△ABC为等腰或直角三角形．【答案】　(1)A　(2)等腰或直角三角形【迁移探究】　(变条件)若将本例(1)条件改为“2sin Acos B＝sin C”，试判断△ABC的形状．解：法一：由已知得2sin Acos B＝sin C＝sin(A＋B)＝sin Acos B＋cos Asin B，即sin(A－B)＝0，因为－π<A－B<π，所以A＝B，故△ABC为等腰三角形．法二：由正弦定理得2acos B＝c，再由余弦定理得2a·＝c⇒a2＝b2⇒a＝b，故△ABC为等腰三角形．判定三角形形状的两种常用途径[提醒]　“角化边”后要注意用因式分解、配方等方法得出边的相应关系；“边化角”后要注意用三角恒等变换公式、三角形内角和定理及诱导公式推出角的关系．1．(2020·陕西西安模拟)在△ABC中，a∶b∶c＝3∶5∶7，那么△ABC是(　　)A．直角三角形  B．钝角三角形C．锐角三角形  D．非钝角三角形解析：选B.因为a∶b∶c＝3∶5∶7，所以可设a＝3t，b＝5t，c＝7t，由余弦定理可得cos C＝＝－，所以C＝120°，△ABC是钝角三角形，故选B.2．(2020·河北衡水中学三调)在△ABC中，角A，B，C所对的边分别为a，b，c，且b2＋c2＝a2＋bc，若sin Bsin C＝sin2A，则△ABC的形状是(　　)A．等腰三角形  B．直角三角形C．等边三角形  D．等腰直角三角形解析：选C.在△ABC中，因为b2＋c2＝a2＋bc，所以cos A＝＝＝，因为A∈(0，π)，所以A＝，因为sin Bsin C＝sin2A，所以bc＝a2，代入b2＋c2＝a2＋bc，得(b－c)2＝0，解得b＝c，所以△ABC的形状是等边三角形，故选C.核心素养系列11　数学运算——计算三角形中的未知量数学运算是在明确运算对象的基础上，依据运算法则解决数学问题的过程．主要包括：理解运算对象、掌握运算法则、探究运算方向、选择运算方法、设计运算程序、求得运算结果等． (2019·高考北京卷)在△ABC中，a＝3，b－c＝2，cos B＝－.(1)求b，c的值；(2)求sin(B＋C)的值．【解】　(1)由余弦定理b2＝a2＋c2－2accos B，得b2＝32＋c2－2×3×c×.因为b＝c＋2，所以(c＋2)2＝32＋c2－2×3×c×.解得c＝5.所以b＝7.(2)由cos B＝－得sin B＝.由正弦定理得sin A＝sin B＝.在△ABC中，B＋C＝π－A.所以sin(B＋C)＝sin A＝.本题第(1)问利用余弦定理得到关于b，c的一个方程，结合b－c＝2可求出b，c的值；第(2)问利用正弦定理求出sin A的值，由同角三角函数关系求出sin(B＋C)的值体现核心素养中的数学运算．　在△ABC中，角A，B，C的对边分别为a，b，c.(1)若a＝3c，b＝，cos B＝，求c的值；(2)若＝，求cos B的值．解：(1)因为a＝3c，b＝，cos B＝，由余弦定理cos B＝，得＝，即c2＝.所以c＝.(2)因为＝，由正弦定理＝，得＝，所以cos B＝2sin B.从而cos2B＝(2sin B)2，即cos2B＝4(1－cos2B)，故cos2B＝.因为sin B>0，所以cos B＝2sin B>0，从而cos B＝.[基础题组练]1．设△ABC的内角A，B，C的对边分别为a，b，c.若a＝2，c＝2，cos A＝且b<c，则b＝(　　)A．3　　　　　　　　　 B．2C．2  D．解析：选C.由余弦定理b2＋c2－2bccos A＝a2，得b2－6b＋8＝0，解得b＝2或b＝4，因为b<c＝2，所以b＝2.选C.2．在△ABC中，已知a＝2，b＝，A＝45°，则满足条件的三角形有(　　)A．一个  B．两个C．0个  D．无法确定解析：选B.由正弦定理得sin B＝＝＝，因为b>a，所以B＝60°或120°，故满足条件的三角形有两个．3．(2020·湖南省湘东六校联考)在△ABC中，A，B，C的对边分别为a，b，c，其中b2＝ac，且sin C＝sin B，则其最小内角的余弦值为(　　)A．－   B.C.  D．解析：选C.由sin C＝sin B及正弦定理，得c＝b.又b2＝ac，所以b＝a，所以c＝2a，所以A为△ABC的最小内角．由余弦定理，知cos A＝＝＝，故选C.4．在△ABC中，a，b，c分别是角A，B，C的对边，以下四个结论中，正确的是(　　)A．若a＞b＞c，则sin A＞sin B＞sin CB．若A＞B＞C，则sin A<sin B<sin CC．acos B＋bcos A＝csin CD．若a2＋b2＜c2，则△ABC是锐角三角形解析：选A.对于A，由于a＞b＞c，由正弦定理＝＝＝2R，可得sin A＞sin B＞sin C，故A正确；对于B，A＞B＞C，由大边对大角定理可知，则a＞b＞c，由正弦定理＝＝＝2R，可得sin A＞sin B＞sin C，故B错误；对于C，根据正弦定理可得acos B＋bcos A＝2R(sin A·cos B＋sin Bcos A)＝2Rsin(B＋A)＝2Rsin(π－C)＝2Rsin C＝c，故C错误；对于D，a2＋b2＜c2，由余弦定理可得cos C＝＜0，由C∈(0，π)，可得C是钝角，故D错误．5．(2020·长春市质量监测(一))在△ABC中，内角A，B，C的对边分别为a，b，c，若b＝acos C＋c，则角A等于(　　)A．60°  B．120°C．45°  D．135°解析：选A.法一：由b＝acos C＋c及正弦定理，可得sin B＝sin Acos C＋sin C，即sin(A＋C)＝sin Acos C＋sin C，即sin Acos C＋cos Asin C＝sin Acos C＋sin C，所以cos Asin C＝sin C，又在△ABC中，sin C≠0，所以cos A＝，所以A＝60°，故选A.法二：由b＝acos C＋c及余弦定理，可得b＝a·＋c，即2b2＝b2＋a2－c2＋bc，整理得b2＋c2－a2＝bc，于是cos A＝＝，所以A＝60°，故选A.6．在△ABC中，角A，B，C满足sin Acos C－sin Bcos C＝0，则三角形的形状为        ．解析：由已知得cos C(sin A－sin B)＝0，所以有cos C＝0或sin A＝sin B，解得C＝90°或A＝B.答案：直角三角形或等腰三角形7．(2019·高考天津卷改编)在△ABC中，内角A，B，C所对的边分别为a，b，c，已知b＋c＝2a，3csin B＝4asin C，则cos B＝        ．解析：在△ABC中，由正弦定理＝，得bsin C＝csin B，又由3csin B＝4asin C，得3bsin C＝4asin C，即3b＝4a.因为b＋c＝2a，得到b＝a，c＝a.由余弦定理可得cos B＝＝＝－.答案：－8．(2020·河南期末改编)在△ABC中，B＝，AC＝，且cos2C－cos2A－sin2B＝－sin Bsin C，则C＝        ，BC＝        ．解析：由cos2C－cos2A－sin2B＝－sin Bsin C，可得1－sin2C－(1－sin2A)－sin2B＝－sin Bsin C，即sin2A－sin2C－sin2B＝－sin Bsin C．结合正弦定理得BC2－AB2－AC2＝－·AC·AB，所以cos A＝，A＝，则C＝π－A－B＝.由＝，解得BC＝.答案：　9．(2020·江西赣州模拟)已知在△ABC中，角A，B，C的对边分别为a，b，c，且asin B＋bcos A＝0.(1)求角A的大小；(2)若a＝2，b＝2，求边c的长．解：(1)因为asin B＋bcos A＝0，所以sin Asin B＋sin Bcos A＝0，即sin B(sin A＋cos A)＝0，由于B为三角形的内角，所以sin A＋cos A＝0，所以sin＝0，而A为三角形的内角，所以A＝.(2)在△ABC中，a2＝c2＋b2－2cbcos A，即20＝c2＋4－4c，解得c＝－4(舍去)或c＝2.10．在△ABC中，A＝2B.(1)求证：a＝2bcos B；(2)若b＝2，c＝4，求B的值．解：(1)证明：因为A＝2B，所以由正弦定理＝，得＝，所以a＝2bcos  B.(2)由余弦定理，a2＝b2＋c2－2bccos A，因为b＝2，c＝4，A＝2B，所以16cos2B＝4＋16－16cos 2B，所以cos2B＝，因为A＋B＝2B＋B<π，所以B<，所以cos B＝，所以B＝.[综合题组练]1．在△ABC中，B＝，BC边上的高等于BC，则cos A＝(　　)A.   B.C．－  D．－解析：选C.如图，过点A作AD⊥BC.设BC＝a，则BC边上的高AD＝a.又因为B＝，所以BD＝AD＝a，AB＝a，DC＝a－BD＝a，所以AC＝＝a.在△ABC中，由余弦定理得cos A＝＝＝－.2．(2020·郑州市调研测试)已知△ABC的内角A，B，C的对边分别是a，b，c，且＝，若a＋b＝4，则c的取值范围为(　　)A．(0，4)  B．[2，4)C．[1，4)  D．(2，4]解析：选B.根据正弦定理可得＝，即＝，由三角形内角和定理可得sin(A＋B)＝sin C，所以sin2A＋sin2B－sin2C＝sin Asin B，再根据正弦定理可得a2＋b2－c2＝ab.因为a＋b＝4，a＋b≥2，所以ab≤4，(a＋b)2＝16，得a2＋b2＝16－2ab，所以16－2ab－c2＝ab，所以16－c2＝3ab，故16－c2≤12，c2≥4，c≥2，故2≤c＜4，故选B.3．(2020·广东佛山顺德第二次质检)在△ABC中，角A，B，C所对的边分别为a，b，c，2bsin Ccos A＋asin A＝2csin B.(1)证明：△ABC为等腰三角形；(2)若D为BC边上的点，BD＝2DC，且∠ADB＝2∠ACD，a＝3，求b的值．解：(1)证明：因为2bsin Ccos A＋asin A＝2csin B，所以由正弦定理得2bccos A＋a2＝2cb，由余弦定理得2bc·＋a2＝2bc，化简得b2＋c2＝2bc，所以(b－c)2＝0，即b＝c.故△ABC为等腰三角形．(2)法一：由已知得BD＝2，DC＝1，因为∠ADB＝2∠ACD＝∠ACD＋∠DAC，所以∠ACD＝∠DAC，所以AD＝CD＝1.又因为cos∠ADB＝－cos∠ADC，所以＝－，即＝－，得2b2＋c2＝9，由(1)可知b＝c，得b＝.法二：由已知可得CD＝a＝1，由(1)知，AB＝AC，所以∠B＝∠C，又因为∠DAC＝∠ADB－∠C＝2∠C－∠C＝∠C＝∠B，所以△CAB∽△CDA，所以＝，即＝，所以b＝.4．(综合型)在△ABC中，角A，B，C所对的边分别为a，b，c，cos B＝bcos A.(1)求cos B的值；(2)若a＝2，cos C＝－，求△ABC外接圆的半径R.解：(1)因为cos B＝bcos A，所以结合正弦定理，得cos B＝sin Bcos A，所以sin Ccos B＝sin(A＋B)＝sin C．又因为sin C≠0，所以cos B＝.(2)由(1)知，sin B＝＝.因为cos C＝－，所以sin C＝＝，所以sin A＝sin(B＋C)＝sin Bcos C＋cos Bsin C＝×＋×＝，所以R＝·＝×＝.