初中数学沪科版八年级上册15.3 等腰三角形第1课时导学案

这是一份初中数学沪科版八年级上册15.3 等腰三角形第1课时导学案，共4页。

第1课时 等腰三角形的性质


知识要点基础练


知识点1 等边对等角








1.如图,△ABC中,AB=AC,∠B=70°,则∠A=(D)


A.70°B.55°


C.50°D.40°





2.如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,则∠B的大小为(B)





A.40°B.36°


C.30°D.25°


知识点2 等腰三角形“三线合一”





3.如图,在△ABC中,AB=AC,AD⊥BC于点D,则下列结论不一定成立的是(A)


A.AD=BDB.BD=CD


C.∠1=∠2D.∠B=∠C


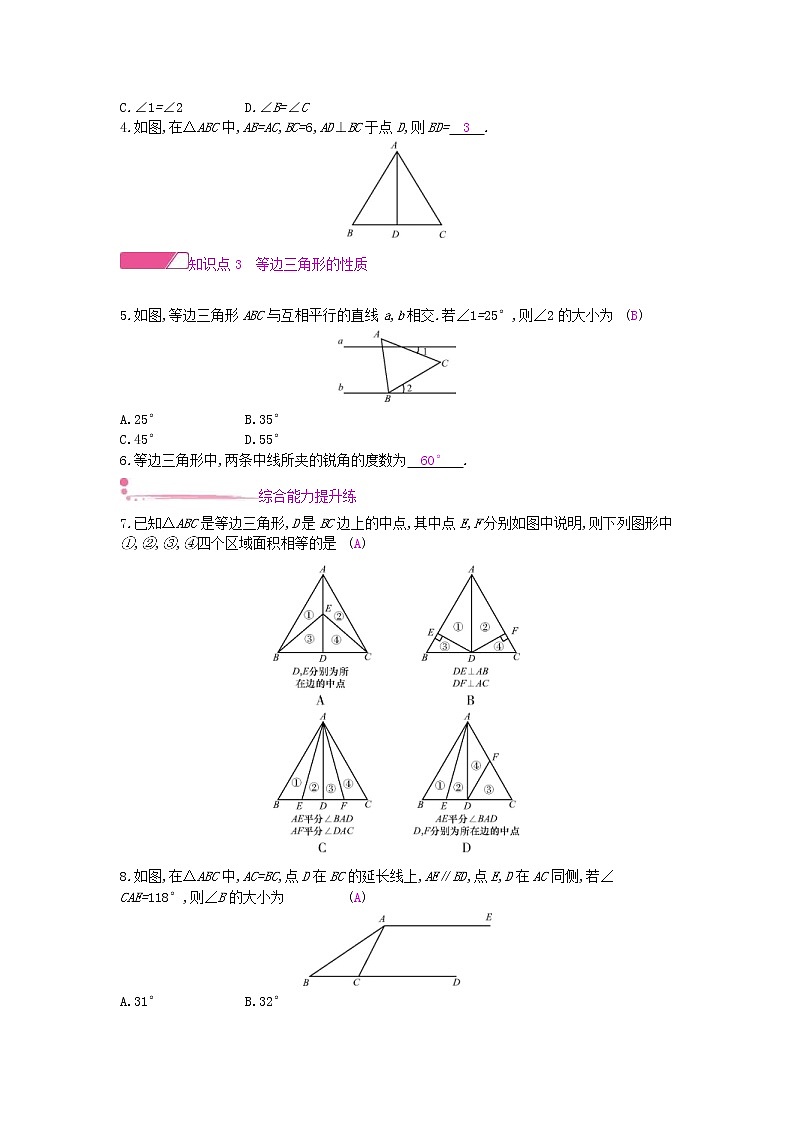
4.如图,在△ABC中,AB=AC,BC=6,AD⊥BC于点D,则BD= 3 .





知识点3 等边三角形的性质





5.如图,等边三角形ABC与互相平行的直线a,b相交.若∠1=25°,则∠2的大小为(B)





A.25°B.35°


C.45°D.55°


6.等边三角形中,两条中线所夹的锐角的度数为 60° .


综合能力提升练


7.已知△ABC是等边三角形,D是BC边上的中点,其中点E,F分别如图中说明,则下列图形中①,②,③,④四个区域面积相等的是(A)





8.如图,在△ABC中,AC=BC,点D在BC的延长线上,AE∥BD,点E,D在AC同侧,若∠CAE=118°,则∠B的大小为(A)





A.31°B.32°


C.59°D.62°


9.在△ABC中,AB=AC=6,由作图痕迹可得DE的长为(B)





A.2B.3C.4D.6


10.如图,△ABC是等边三角形,BD是中线,延长BC到点E,使CE=CD,连接DE.下列四个结论:①BD⊥AC;②BD平分∠ABC;③BD=DE;④∠BDE=120°.其中正确的个数是(D)





A.1B.2C.3D.4


11.如图,∠AOB是角度为10°的钢架,要使钢架更加牢固,需在其内部添加一些钢管EF,FG,GH,…,且OE=EF=FG=GH…,在OA,OB足够长的情况下,最多能添加这样的钢管的根数为 8 .





提示:画图求解,当钢管垂直于OA时,则不能再添加钢管.





12.如图,在△ABC中,AB=AC,D是BC边上的中点,DE,DF分别垂直AB,AC于点E和F.


求证:DE=DF.





证明:在△ABC中,AB=AC,


∴∠B=∠C.


∵D是BC边上的中点,∴BD=DC.


∵DE,DF分别垂直AB,AC于点E和F,


∴∠BED=∠CFD=90°.


在△BED和△CFD中,


∴△BED≌△CFD(AAS),∴DE=DF.





13.如图,已知△ABC中,AB=AC,∠BAC<90°,CD,BE为△ABC的中线,AF⊥CD,AG⊥BE,分别交CD,BE的延长线于F,G两点,试问:


(1)AF与AG相等吗?为什么?


(2)当∠BAC=90°时,其余条件不变,猜想AF = AG(用“>”“<”或“=”填空);当∠BAC>90°时,其余条件不变,猜想AF = AG.(用“>”“<”或“=”填空)


(3)通过本题,你可以得到怎样的结论?请用文字叙述.





解:(1)AF=AG.理由如下:


∵AB=AC,CD,BE为△ABC的中线,∴AD=AE.


在△ADC和△AEB中,


∴△ADC≌△AEB,∴∠ACD=∠ABE.


又∵∠AFC=∠AGB=90°,AC=AB,


∴△ACF≌△ABG,∴AF=AG.


(3)等腰三角形的顶点到两腰中线所在的直线的距离相等.


拓展探究突破练


14.在△ABC中,AB=AC.


(1)①如图1,如果∠BAD=30°,AD是BC边上的高,AD=AE,则∠EDC= 15° ;


②如图2,如果∠BAD=40°,AD是BC上的高,AD=AE,则∠EDC= 20° .


(2)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示.


(3)如图3,如果AD不是BC上的高,AD=AE,是否仍有上述关系?请说明理由.





解:(2)∠BAD=2∠EDC.


(3)仍成立.理由如下:


∵AD=AE,∴∠ADE=∠AED,


∴∠BAD+∠B=∠ADC=∠ADE+∠EDC=∠AED+∠EDC=(∠EDC+∠C)+∠EDC=2∠EDC+∠C.


又∵AB=AC,∴∠B=∠C,∴∠BAD=2∠EDC.