湘教版九年级上册1.2 反比例函数的图像与性质第2课时学案设计

这是一份湘教版九年级上册1.2 反比例函数的图像与性质第2课时学案设计，共10页。学案主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

课时作业(三)





一、选择题


1．已知反比例函数y＝eq \f(k,x)(k≠0)的图象经过点P(2，－3)，则这个函数的图象位于( )


A．第一、三象限 B．第二、四象限


C．第一、二象限 D．第三、四象限


2．关于反比例函数y＝－eq \f(4,x)的图象和性质，下列说法：①必经过点(－1，－4)；②函数值y随x的增大而增大；③两个分支关于x轴对称；④两个分支关于原点对称．其中正确的有( )


eq \a\vs4\al(链接听课例2归纳总结)


A．1个 B．2个 C．3个 D．4个


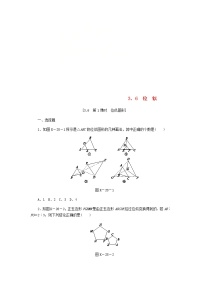
3．已知反比例函数y＝eq \f(kb,x)的图象如图K－3－1所示，则一次函数y＝kx＋b的图象可能是( )





图K－3－1





图K－3－2


4．反比例函数y＝－eq \f(2,x)的图象上有两点P1(x1，y1)，P2(x2，y2)．若x1＜0＜x2，则下列结论正确的是( )


A．y1＜y2＜0 B．y1＜0＜y2


C．y1＞y2＞0 D．y1＞0＞y2


5．2017·黔东南州反比例函数y＝－eq \f(3,x)(x＜0)的图象如图K－3－3，则矩形OAPB的面积是( )





图K－3－3


A．3 B．－3 C.eq \f(3,2) D．－eq \f(3,2)


6．如图K－3－4，A为反比例函数y＝eq \f(k,x)图象上的一点，AB⊥y轴于点B，点P在x轴上，S△ABP＝2，则这个反比例函数的表达式为( )





图K－3－4


A．y＝eq \f(2,x) B．y＝－eq \f(2,x)


C．y＝eq \f(4,x) D．y＝－eq \f(4,x)


二、填空题


7．已知反比例函数y＝eq \f(m＋2,x)，当x＞0时，y随x的增大而增大，则m的取值范围是________．


8．如图K－3－5所示，点A在双曲线y＝eq \f(k,x)上，AB⊥x轴于点B，且△AOB的面积为2，则k＝________．





图K－3－5


9．已知反比例函数y＝eq \f(k,x)的图象经过点(3，－1)，则当1＜y＜3时，自变量x的取值范围是________．


10．如图K－3－6，有反比例函数y＝eq \f(1,x)，y＝－eq \f(1,x)的图象和一个以原点为圆心，2为半径的圆，则S阴影＝________．





图K－3－6


三、解答题


11．已知y是x的反比例函数，且当x＝2时，y＝－3，


(1)求y与x之间的函数表达式；


(2)画出这个函数的图象；


(3)试判断点P(－2，3)是否在这个函数的图象上.eq \a\vs4\al(链接听课例1归纳总结)





图K－3－7














12．已知函数y＝(k－2)xk2－5为反比例函数．


(1)求k的值；eq \a\vs4\al(链接听课例2归纳总结)


(2)它的图象在第________象限内，在各象限内，y随x的增大而________(填变化情况)；


(3)求出－2≤x≤－eq \f(1,2)时，y的取值范围．





























13．已知反比例函数的图象经过点P(2，－3)．


(1)求该函数的表达式；


(2)若将点P沿x轴负方向平移3个单位，再沿y轴方向平移n(n＞0)个单位得到点P′，使点P′恰好在该函数的图象上，求n的值和点P沿y轴平移的方向．
































14.如图K－3－8，点A在反比例函数y＝eq \f(k,x)的图象在第二象限内的分支上，AB⊥x轴于点B，O是原点，且△AOB的面积为1.试解答下列问题：


(1)比例系数k＝________；


(2)在给定直角坐标系中，画出这个函数图象的另一个分支；


(3)当x＞1时，写出y的取值范围．


eq \a\vs4\al(链接听课例3归纳总结)





图K－3－8

















新定义问题定义：如图K－3－9，若双曲线y＝eq \f(k,x)(k＜0)与它的其中一条对称轴y＝－x相交于两点A，B，则线段AB的长称为双曲线y＝eq \f(k,x)(k＜0)的对径．


(1)求双曲线y＝－eq \f(1,x)的对径；


(2)若某双曲线y＝eq \f(k,x)(k＜0)的对径是10 eq \r(2)，求k的值．





图K－3－9











详解详析


【作业高效训练】


[课堂达标]


1．[解析] B 因为图象经过点P(2，－3)，所以－3＝eq \f(k,2)，即k＝－6<0，故这个函数的图象分布在第二、四象限．


2．[答案] A


3．[答案] C


4．[解析] D ∵反比例函数y＝－eq \f(2,x)中k＝－2＜0，∴此函数图象在第二、四象限．∵x1＜0＜x2，∴点A(x1，y1)在第二象限，点B(x2，y2)在第四象限，∴y1＞0＞y2.


5．[解析] A ∵点P在反比例函数y＝－eq \f(3,x)(x＜0)的图象上，∴可设P(x，－eq \f(3,x))，∴OA＝－x，PA＝－eq \f(3,x)，∴S矩形OAPB＝OA·PA＝－x·(－eq \f(3,x))＝3，故选A.


6．[解析] D 连接OA.∵△AOB的面积＝△ABP的面积＝2，△AOB的面积＝eq \f(1,2)|k|，∴eq \f(1,2)|k|＝2，∴k＝±4.又∵反比例函数的图象的一支位于第二象限，∴k＜0，∴k＝－4，∴这个反比例函数的表达式为y＝－eq \f(4,x)，故选D.


7．[答案] m＜－2


8．[答案] －4


[解析] ∵反比例函数的图象在第二、四象限，∴k＜0.∵S△AOB＝2，∴|k|＝4，∴k＝－4.故答案为－4.


9．[答案] －3＜x＜－1


[解析] ∵反比例函数y＝eq \f(k,x)的图象经过点(3，－1)，∴k＝3×(－1)＝－3，


∴反比例函数的表达式为y＝－eq \f(3,x).


∵反比例函数y＝－eq \f(3,x)中k＝－3<0，


∴该反比例函数的图象在第二、四象限，且在每个象限内y随x的增大而增大．


当y＝1时，x＝－3；


当y＝3时，x＝－1.


∴当1＜y＜3时，自变量x的取值范围是－3＜x＜－1.


10．[答案] 2π


11．解：(1)设反比例函数的表达式为y＝eq \f(k,x)，把x＝2，y＝－3代入得k＝2×(－3)＝－6，所以反比例函数的表达式为y＝－eq \f(6,x).


(2)如图所示：





(3)当x＝－2时，y＝－eq \f(6,x)＝3，所以点P(－2，3)在反比例函数y＝－eq \f(6,x)的图象上．


12．解：(1)由题意得k2－5＝－1，解得k＝±2.


∵k－2≠0，∴k＝－2.


(2)∵k－2＝－4＜0，


∴反比例函数的图象在第二、四象限，在各象限内，y随着x的增大而增大．


故答案为二、四；增大．


(3)∵反比例函数的表达式为y＝－eq \f(4,x)，


∴当x＝－2时，y＝2；当x＝－eq \f(1,2)时，y＝8，


∴当－2≤x≤－eq \f(1,2)时，2≤y≤8.


13．解：(1)设该反比例函数的表达式为y＝eq \f(k,x)，


∵图象经过点P(2，－3)，


∴k＝2×(－3)＝－6，


∴该反比例函数的表达式为y＝－eq \f(6,x).


(2)∵点P沿x轴负方向平移3个单位，


∴点P′的横坐标为2－3＝－1，


当x＝－1时，y＝－eq \f(6,－1)＝6，


∴n＝6－(－3)＝9，点P沿y轴平移的方向为向上．


14．解：(1)由于△AOB的面积为1，则|k|＝2.


又函数图象的一支位于第二象限，所以k<0，


则k＝－2.


(2)如图所示：








(3)利用函数图象可得出：当x＞1时，－2＜y＜0.


[素养提升]


[全品导学号：90912161] 解：过点A作AC⊥x轴于点C，如图．


(1)解方程组eq \b\lc\{(\a\vs4\al\c1(y＝－\f(1,x)，,y＝－x，))得eq \b\lc\{(\a\vs4\al\c1(x1＝－1，,y1＝1，))eq \b\lc\{(\a\vs4\al\c1(x2＝1，,y2＝－1，))


∴点A的坐标为(－1，1)，点B的坐标为(1，－1)，


∴OC＝AC＝1，


∴OA＝eq \r(2)OC＝eq \r(2).


∵双曲线y＝eq \f(k,x)和直线y＝－x均是中心对称图形，


∴AB＝2OA＝2 eq \r(2)，


∴双曲线y＝－eq \f(1,x)的对径是2 eq \r(2).





(2)∵双曲线的对径为10 eq \r(2)，


即AB＝10 eq \r(2)，


∴OA＝5 eq \r(2).


∵OA＝eq \r(2)OC＝eq \r(2)AC，


∴OC＝AC＝5，


∴点A的坐标为(－5，5)．


把A(－5，5)代入双曲线y＝eq \f(k,x)(k<0)，得k＝－5×5＝－25，


即k的值为－25.