初中数学北师大版九年级上册2 矩形的性质与判定教案配套ppt课件

这是一份初中数学北师大版九年级上册2 矩形的性质与判定教案配套ppt课件，共24页。PPT课件主要包含了学习目标，∴ACBD，又∵ACBD，同学们自己去解答吧等内容，欢迎下载使用。
1．回顾矩形的性质及判定方法．2．矩形的性质和判定方法与其他有关知识的综合运用.(难点)
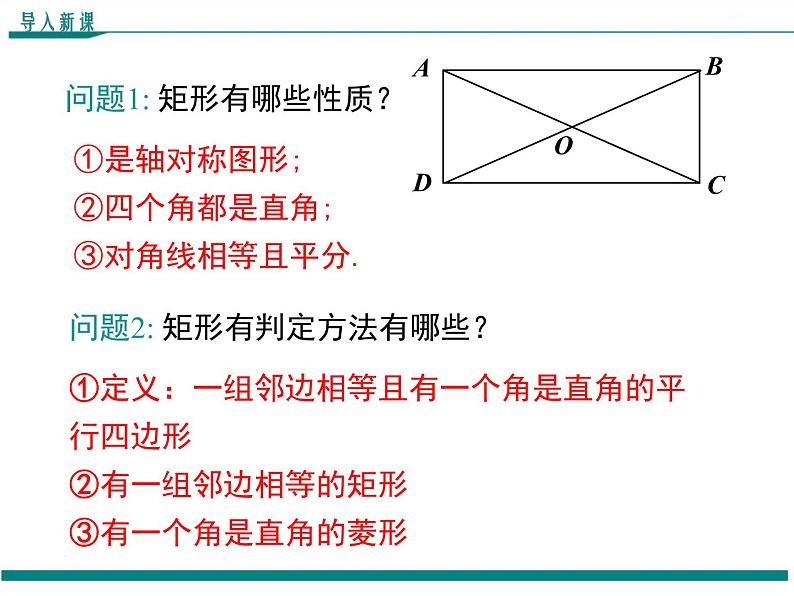
问题1: 矩形有哪些性质？
①是轴对称图形; ②四个角都是直角;③对角线相等且平分.
①定义：一组邻边相等且有一个角是直角的平行四边形②有一组邻边相等的矩形 ③有一个角是直角的菱形
问题2: 矩形有判定方法有哪些？
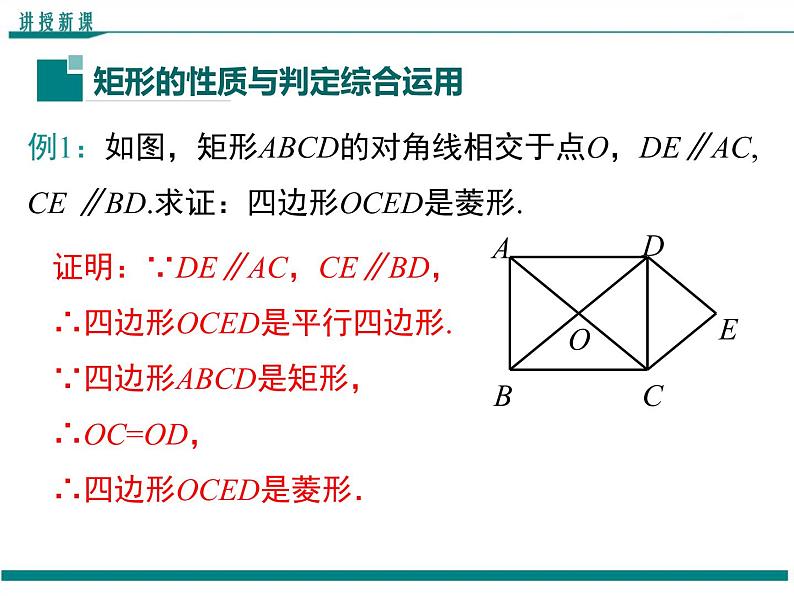
例1：如图，矩形ABCD的对角线相交于点O，DE∥AC,CE ∥BD.求证：四边形OCED是菱形.
证明：∵DE∥AC，CE∥BD，∴四边形OCED是平行四边形.∵四边形ABCD是矩形，∴OC=OD，∴四边形OCED是菱形．
证明：连接AC、BD.
∵四边形ABCD是矩形，
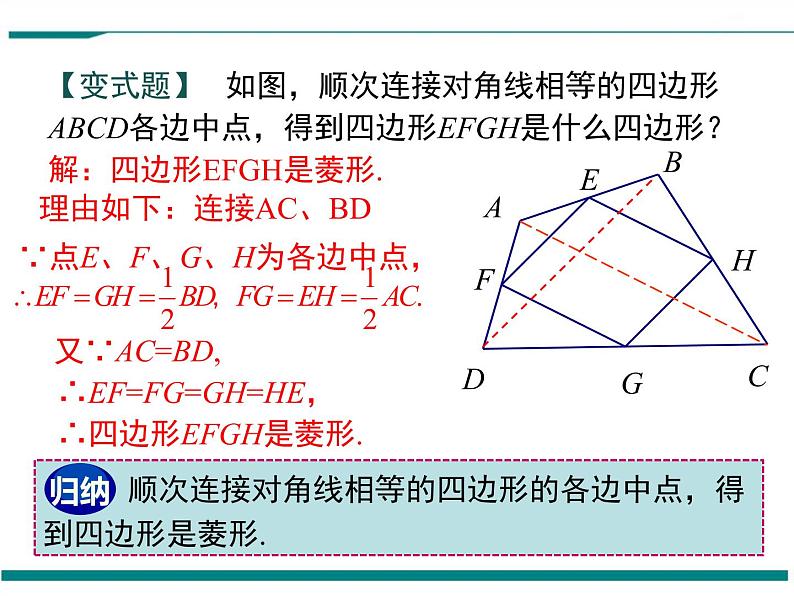
∵点E、F、G、H为各边中点，
∴EF=FG=GH=HE，
∴四边形EFGH是菱形.
例2 如图，顺次连接矩形ABCD各边中点，得到四边形EFGH，求证：四边形EFGH是菱形.
【变式题】 如图，顺次连接对角线相等的四边形ABCD各边中点，得到四边形EFGH是什么四边形？
解：四边形EFGH是菱形.
顺次连接对角线相等的四边形的各边中点，得到四边形是菱形.
理由如下：连接AC、BD
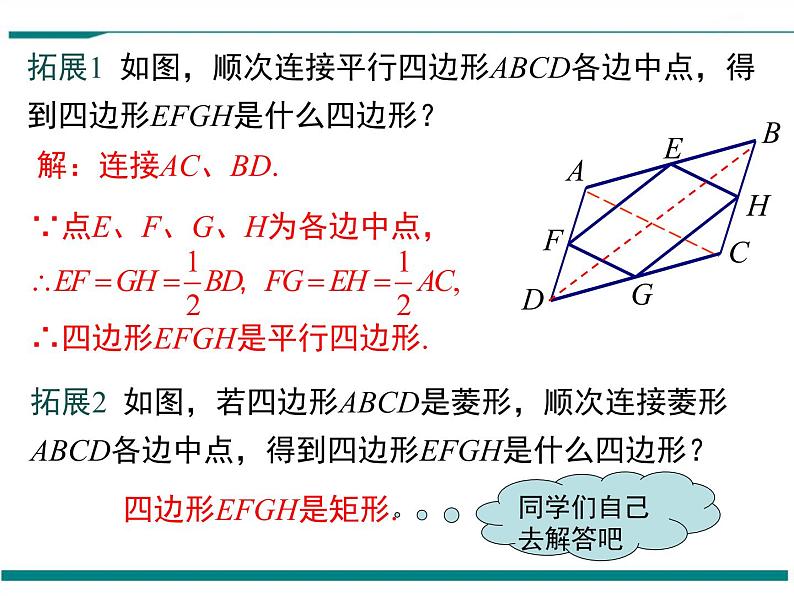
拓展1 如图，顺次连接平行四边形ABCD各边中点，得到四边形EFGH是什么四边形？
∴四边形EFGH是平行四边形.
拓展2 如图，若四边形ABCD是菱形，顺次连接菱形ABCD各边中点，得到四边形EFGH是什么四边形？
四边形EFGH是矩形.
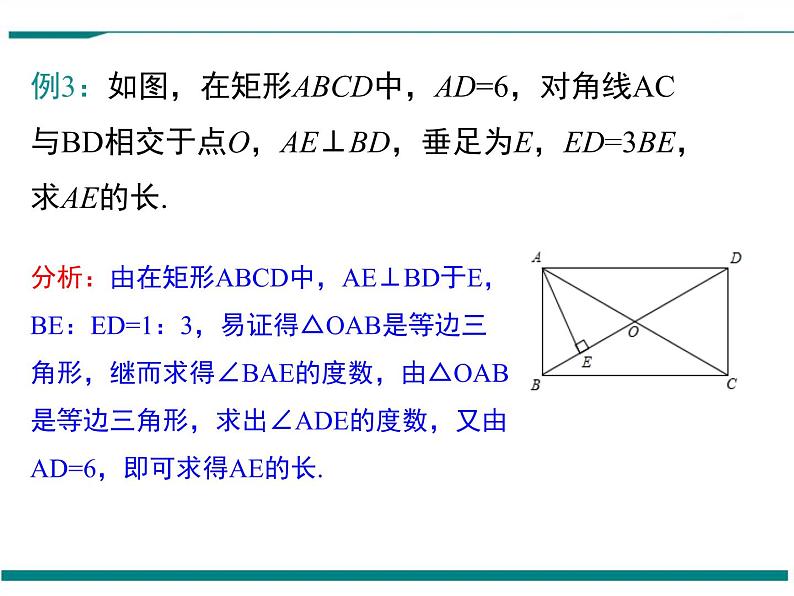
例3：如图，在矩形ABCD中，AD=6，对角线AC与BD相交于点O，AE⊥BD，垂足为E，ED=3BE，求AE的长.
分析：由在矩形ABCD中，AE⊥BD于E，BE：ED=1：3，易证得△OAB是等边三角形，继而求得∠BAE的度数，由△OAB是等边三角形，求出∠ADE的度数，又由AD=6，即可求得AE的长.
解：∵四边形ABCD是矩形，∴OB=OD，OA=OC，AC=BD，∴OA=OB，∵BE：ED=1：3，∴BE：OB=1：2，∵AE⊥BD，∴AB=OA，∴OA=AB=OB，即△OAB是等边三角形，∴∠ABD=60°，∴∠ADE=90°-∠ABD=30°，∴AE= AD=3.
例4：已知：如图，在△ABC中，AB=AC，AD是△ABC的一条角平分线，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E．（1）求证：四边形ADCE为矩形；（2）连接DE，交AC于点F，请判断 四边形ABDE的形状，并证明；（3）线段DF与AB有怎样的关系？请直接写出你的结论.
证明：∵在△ABC中，AB=AC，AD是BC边的中线，∴AD⊥BC，∠BAD=∠CAD，∴∠ADC=90°，∵AN为△ABC的外角∠CAM的平分线，∴∠MAN=∠CAN，∴∠DAE=90°，∵CE⊥AN，∴∠AEC=90°，∴四边形ADCE为矩形；
（1）求证：四边形ADCE为矩形；
解：四边形ABDE是平行四边形，理由如下：由（1）知，四边形ADCE为矩形，则AE=CD，AC=DE．又∵AB=AC，BD=CD，∴AB=DE，AE=BD，∴四边形ABDE是平行四边形；
（2）连接DE，交AC于点F，请判断四边形ABDE的形状，并证明；
解：DF∥AB，DF= AB．理由如下：∵四边形ADCE为矩形，∴AF=CF，∵BD=CD，∴DF是△ABC的中位线，∴DF∥AB，DF= AB
(3)线段DF与AB有怎样的关系？请直接写出你的结论.
【点评】此题考查了矩形的判定与性质、三线合一以及三角形中位线的性质．此题难度适中，注意掌握数形结合思想的应用.
例5：如图所示，在△ABC中，D为BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，且AF＝BD.连接BF.(1)BD与DC有什么数量关系？请说明理由；(2)当△ABC满足什么条件时，四边形AFBD是矩形？并说明理由．
解：(1)BD＝CD.理由如下：∵AF∥BC，∴∠AFE＝∠DCE.∵E是AD的中点，∴AE＝DE.在△AEF和△DEC中，∴△AEF≌△DEC(AAS)，∴AF＝DC.∵AF＝BD，∴BD＝DC；
(2)当△ABC满足AB＝AC时，四边形AFBD是矩形．理由如下：∵AF∥BD，AF＝BD，∴四边形AFBD是平行四边形．∴AB＝AC，BD＝DC，∴∠ADB＝90°.∴四边形AFBD是矩形．
【方法总结】本题综合考查了矩形和全等三角形的判定方法，明确有一个角是直角的平行四边形是矩形是解本题的关键．
1.如图，四边形ABCD和四边形AEFC是两个矩形，点B在EF边上，若矩形ABCD和矩形AEFC的面积分别是S1，S2，则S1，S2的大小关系是(　 　)A．S1>S2　　　　　　　B．S1＝S2C．S1