北师大版九年级上册第一章 特殊平行四边形综合与测试复习ppt课件

这是一份北师大版九年级上册第一章 特殊平行四边形综合与测试复习ppt课件，共22页。PPT课件主要包含了平行且相等，平行且四边相等，四个角都是直角，对角相等邻角互补，互相平分且相等，要点梳理，考点讲练等内容，欢迎下载使用。

互相垂直平分且相等，每一条对角线平分一组对角
互相垂直且平分，每一条对角线平分一组对角
一、菱形、矩形、正方形的性质
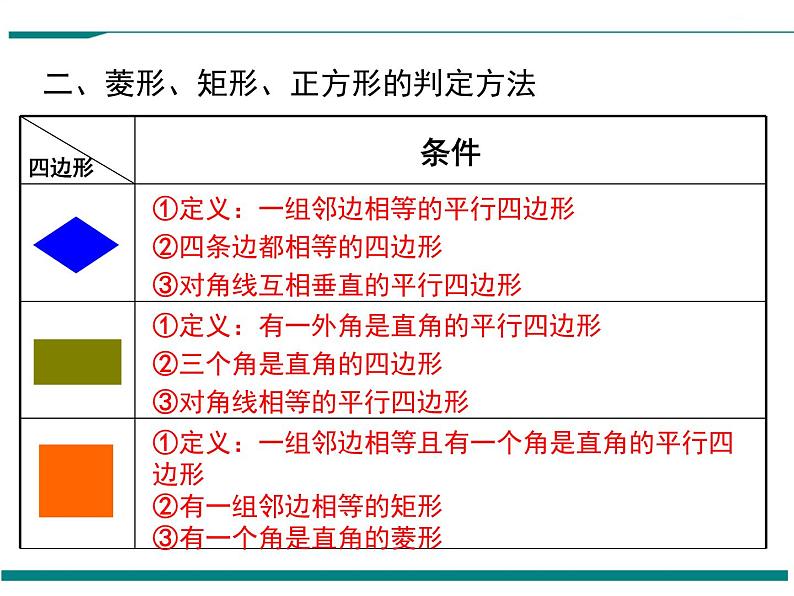
①定义：有一外角是直角的平行四边形 ②三个角是直角的四边形③对角线相等的平行四边形
①定义：一组邻边相等的平行四边形 ②四条边都相等的四边形③对角线互相垂直的平行四边形
①定义：一组邻边相等且有一个角是直角的平行四边形②有一组邻边相等的矩形③有一个角是直角的菱形
二、菱形、矩形、正方形的判定方法
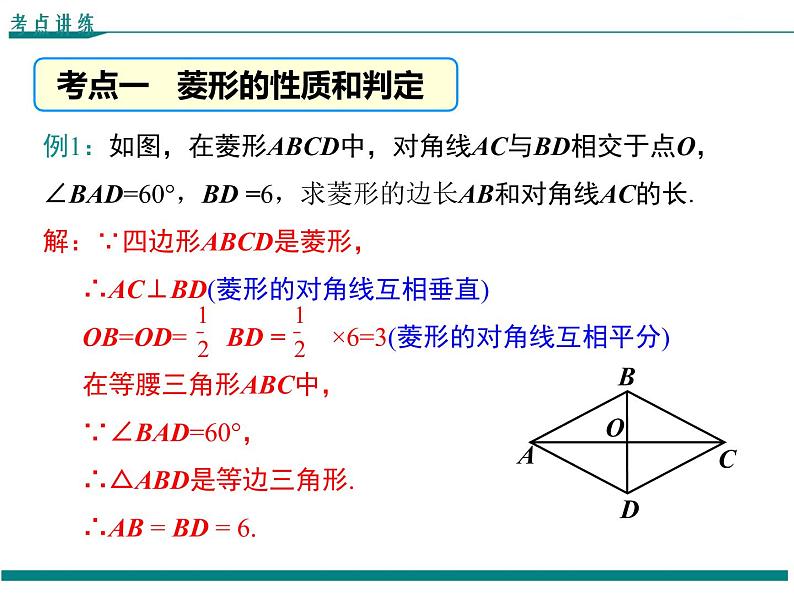
例1：如图，在菱形ABCD中，对角线AC与BD相交于点O，∠BAD=60°，BD =6，求菱形的边长AB和对角线AC的长.解：∵四边形ABCD是菱形， ∴AC⊥BD(菱形的对角线互相垂直) OB=OD= BD = ×6=3(菱形的对角线互相平分)在等腰三角形ABC中，∵∠BAD=60°，∴△ABD是等边三角形.∴AB = BD = 6.
证明：在△AOB中.∵AB= , OA=2,OB=1. ∴AB2=AO2+OB2. ∴ △AOB是直角三角形, ∠AOB是直角. ∴AC⊥BD.∴ □ABCD是菱形 (对角线垂直的平行四边形是菱形).
1. 已知：如右图,在□ABCD中,对角线AC与BD相交于点O, AB= ,OA=2,OB=1. 求证： □ABCD是菱形.
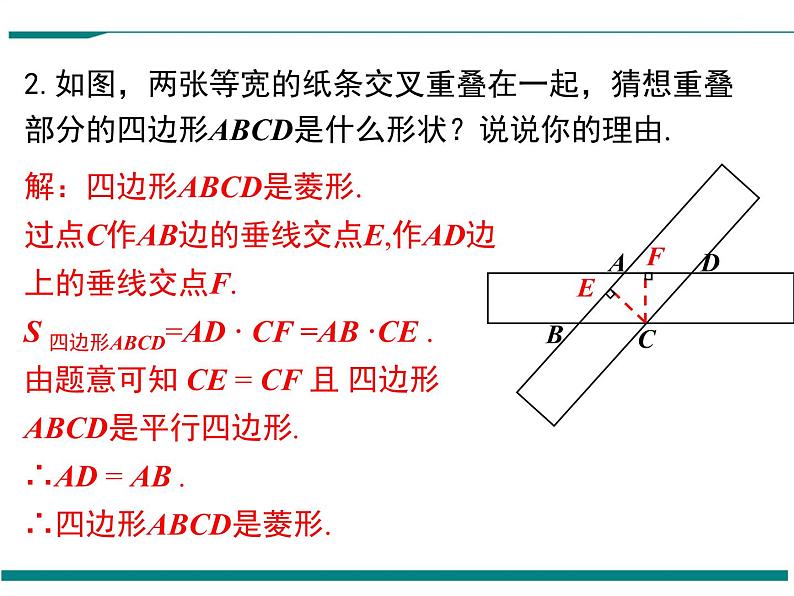
2.如图，两张等宽的纸条交叉重叠在一起，猜想重叠部分的四边形ABCD是什么形状？说说你的理由.
解：四边形ABCD是菱形.过点C作AB边的垂线交点E,作AD边上的垂线交点F.S 四边形ABCD=AD · CF =AB ·CE .由题意可知 CE = CF 且 四边形ABCD是平行四边形.∴AD = AB . ∴四边形ABCD是菱形.
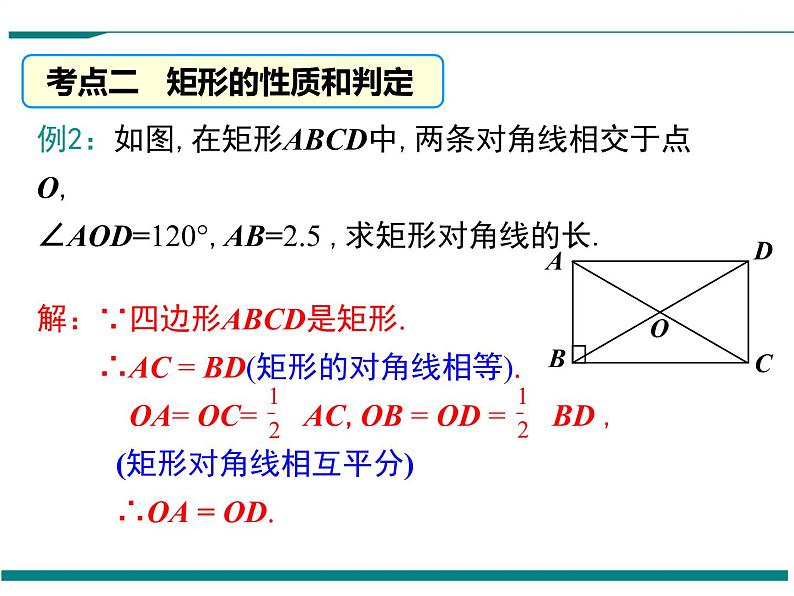
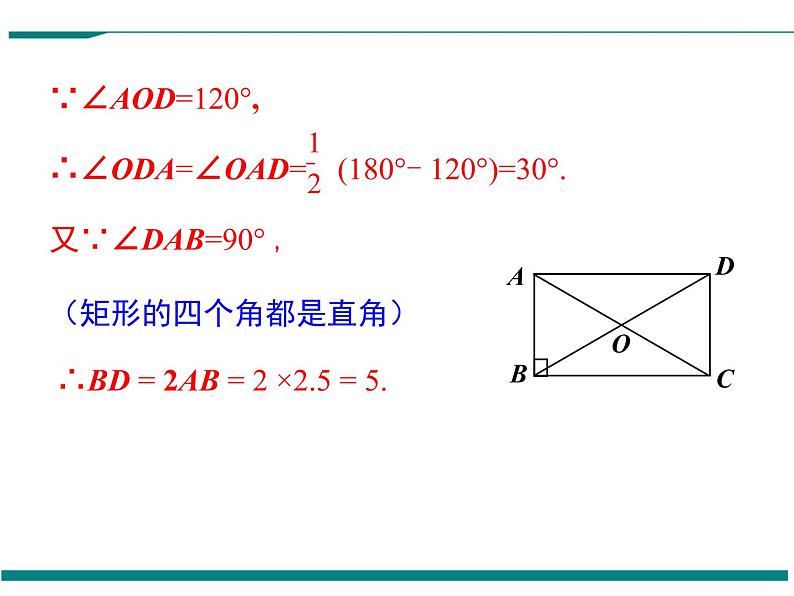
例2：如图,在矩形ABCD中,两条对角线相交于点O,∠AOD=120°,AB=2.5 ,求矩形对角线的长.
解：∵四边形ABCD是矩形. ∴AC = BD(矩形的对角线相等). OA= OC= AC,OB = OD = BD ,(矩形对角线相互平分)∴OA = OD.
∵∠AOD=120°,∴∠ODA=∠OAD= (180°- 120°)=30°.又∵∠DAB=90° ,（矩形的四个角都是直角） ∴BD = 2AB = 2 ×2.5 = 5.
例3 如图，在矩形ABCD中，对角线AC与BD相交于点O，过点A作AE∥BD，过点D作ED∥AC，两线相交于点E．求证：四边形AODE是菱形；
证明：∵AE∥BD，ED∥AC，∴四边形AODE是平行四边形.∵四边形ABCD是矩形，∴AC=BD，OA=OC= AC， OB=OD= BD，∴OA=OC=OD，∴四边形AODE是菱形.
【变式题】如图，O是菱形ABCD对角线的交点，作BE∥AC，CE∥BD，BE、CE交于点E，四边形CEBO是矩形吗？说出你的理由.
解：四边形CEBO是矩形.理由如下：已知四边形ABCD是菱形. ∴AC⊥BD. ∴∠BOC=90°. ∵BE∥AC,CE∥BD， ∴四边形CEBO是平行四边形. ∴四边形CEBO是矩形.
3.如图,在□ABCD中,对角线AC与BD相交于点O , △ABO是等边三角形, AB=4,求□ABCD的面积.解：∵四边形ABCD是平行四边形,∴OA= OC,OB = OD.又∵△ABO是等边三角形,∴OA= OB=AB= 4,∠BAC=60°.∴AC= BD= 2OA = 2×4 = 8.
∴□ABCD是矩形 （对角线相等的平行四边形是矩形）.∴∠ABC=90°（矩形的四个角都是直角） . 在Rt△ABC中,由勾股定理,得AB2 + BC2 =AC2 , ∴BC= .∴S□ABCD=AB·BC=4× =
4.如图，O是菱形ABCD对角线的交点，作BE∥AC，CE∥BD，BE、CE交于点E，四边形CEBO是矩形吗？说出你的理由.
解：四边形CEBO是矩形.理由如下：已知四边形ABCD是菱形. ∴AC⊥BD. ∴∠BOC=90°. ∵DE∥AC,CE∥BD， ∴四边形CEBO是平行四边形. ∴四边形CEBO是矩形（有一个角是直角的平行四边形是矩形）.
例4 如图，已知在四边形ABFC中，∠ACB＝90°，BC的垂直平分线EF交BC于点D，交AB于点E，且CF＝AE；(1)试判断四边形BECF是什么四边形？并说明理由；(2)当∠A的大小满足什么条件时，四边形BECF是正方形？请回答并证明你的结论．
解：(1)四边形BECF是菱形．理由如下：∵EF垂直平分BC，∴BF＝FC，BE＝EC，∴∠3＝∠1.∵∠ACB＝90°，∴∠3＋∠4＝90°，∠1＋∠2＝90°,∴∠2＝∠4，
∴EC＝AE，∴BE＝AE.∵CF＝AE，∴BE＝EC＝CF＝BF，∴四边形BECF是菱形；(2)当∠A＝45°时，菱形BECF是正方形．证明如下：∵∠A＝45°，∠ACB＝90°，∴∠CBA＝45°，∴∠EBF＝2∠CBA＝90°，∴菱形BECF是正方形．
正方形的判定方法：①先判定四边形是矩形，再判定这个矩形有一组邻边相等；②先判定四边形是菱形，再判定这个矩形有一个角为直角；③还可以先判定四边形是平行四边形，再用①或②进行判定．
例5 如图，△ABC中，点O是AC上的一动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角∠ACG的平分线于点F，连接AE、AF.(1)求证：∠ECF＝90°；(2)当点O运动到何处时，四边形AECF是矩形？请 说明理由；
(1)证明：∵CE平分∠BCO，CF平分∠GCO，∴∠OCE＝∠BCE，∠OCF＝∠GCF，∴∠ECF＝ ×180°＝90°.
(2)解：当点O运动到AC的中点时，四边形AECF是矩形．理由如下：∵MN∥BC，∴∠OEC＝∠BCE，∠OFC＝∠GCF.又∵CE平分∠BCO，CF平分∠GCO，∴∠OCE＝∠BCE，∠OCF＝∠GCF，∴∠OCE＝∠OEC，∠OCF＝∠OFC，∴EO＝CO，FO＝CO，∴OE＝OF.又∵当点O运动到AC的中点时，AO＝CO，∴四边形AECF是平行四边形.∵∠ECF＝90°，∴四边形AECF是矩形.
解：当点O运动到AC的中点时，且满足∠ACB为直角时，四边形AECF是正方形．∵由(2)知当点O运动到AC的中点时，四边形AECF 是矩形，已知MN∥BC，当∠ACB＝90°，则∠AOF＝∠COE＝∠COF＝∠AOE＝90°，即AC⊥EF，∴四边形AECF是正方形．
(3)在(2)的条件下，△ABC应该满足什么条件时， 四边形AECF为正方形．
5.如图，两个含有30°角的完全相同的三角板ABC和DEF沿直线FC滑动，下列说法错误的是（　　）A．四边形ACDF是平行四边形 B．当点E为BC中点时，四边形ACDF是矩形 C．当点B与点E重合时，四边形ACDF是菱形 D．四边形ACDF不可能是正方形
6.如图，在菱形ABCD中，对角线AC=6，BD=10，则菱形ABCD的面积为______．
7.如图，四边形ABCD是边长为2的正方形，点G是BC延长线上一点，连接AG，点E、F分别在AG上，连接BE、DF，∠1＝∠2，∠3＝∠4.(1)证明：△ABE≌△DAF；(2)若∠AGB＝30°，求EF的长．
(1)证明：∵四边形ABCD是正方形，∴AB＝AD.在△ABE和△DAF中， ∴△ABE≌△DAF.
(2) 解：∵四边形ABCD是正方形，∴∠1＋∠4＝90°.∵∠3＝∠4，∴∠1＋∠3＝90°，∴∠AFD＝90°.在正方形ABCD中， AD∥BC，∴∠1＝∠AGB＝30°.在Rt△ADF中，∠AFD＝90°，AD＝2，∴AF＝ ，DF＝1.由(1)得△ABE≌△DAF，∴AE＝DF＝1，∴EF＝AF－AE＝ －1.