北师大版九年级上册1 认识一元二次方程教课内容ppt课件

这是一份北师大版九年级上册1 认识一元二次方程教课内容ppt课件，共23页。PPT课件主要包含了3x+3y36，5x+10，x+25x-2，x20，x2x3+x2-1，x25x-1，≠±1，＝－1等内容，欢迎下载使用。

1.理解一元二次方程的概念.（难点）2.根据一元二次方程的一般形式，确定各项系数.3.理解并灵活运用一元二次方程概念解决有关问题.(重点）
2.什么叫方程？我们学过哪些方程？
含有未知数的等式叫做方程.
我们学过的方程有一元一次方程，二元一次方程（组）及分式方程，其中前两种方程是整式方程.
3.什么叫一元一次方程？
含有一个未知数，且未知数的次数是1的整式方程叫做一元一次方程.
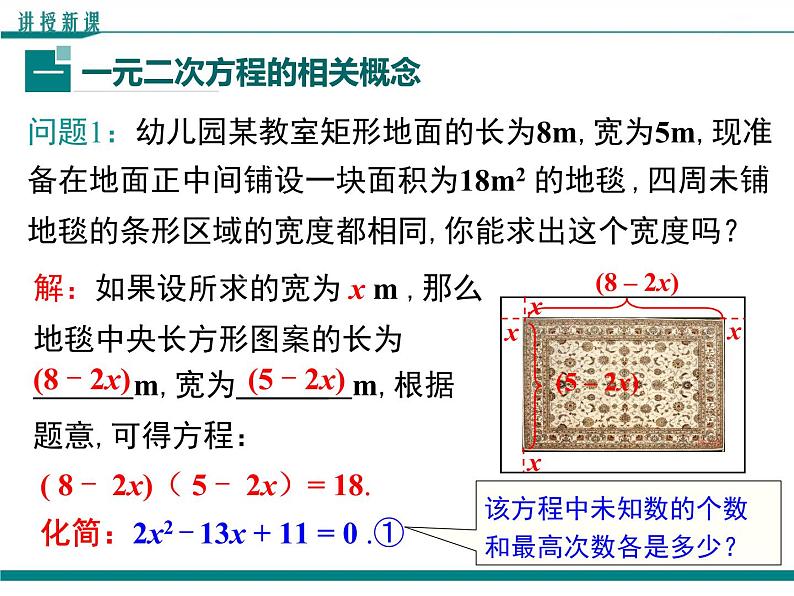
问题1：幼儿园某教室矩形地面的长为8m,宽为5m,现准备在地面正中间铺设一块面积为18m2 的地毯 ,四周未铺地毯的条形区域的宽度都相同,你能求出这个宽度吗？
解：如果设所求的宽为 x m ,那么地毯中央长方形图案的长为 m,宽为　　　 m,根据题意,可得方程：
( 8 - 2x)（ 5 - 2x）= 18.化简：2x2 - 13x + 11 = 0 .①
该方程中未知数的个数和最高次数各是多少？
问题2：观察下面等式：102 + 112 + 122 = 132 + 142 你还能找到其他的五个连续整数，使前三个数的平方和等于后两个数的平方和吗？
解：如果设五个连续整数中的第一个数为x，那么后面四个数依次可表示为： , , , .　根据题意，可得方程： 　　　　　　　　　　　　　　　　　　　　　　
x2 + (x + 1)2 + (x + 2)2 = (x + 3)2 + (x + 4)2.化简得，x2 - 8x - 20＝0. ②
解：由勾股定理可知,滑动前梯子底端距墙　　　　m.如果设梯子底端滑动x m ,那么滑动后梯子底端距墙　　 m ,根据题意，可得方程：
问题3：如图，一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.如果梯子的顶端下滑1m,那么梯子的底端滑动多少米？
72 + (x + 6)2 = 102.化简得，x2 + 12 x - 15 = 0. ③
① 2x2 - 13x + 11 = 0 ；② x2 - 8x - 20＝0；③ x2 + 12 x - 15 = 0.
1.只含有一个未知数; 2.未知数的最高次数是2; 3.整式方程．
方程①、 ②、 ③都不是一元一次方程.那么这两个方程与一元一次方程的区别在哪里？它们有什么共同特点呢？
只含有一个未知数x的整式方程，并且都可以化为ax2+bx+c=0(a,b,c为常数, a≠0)的形式，这样的方程叫做一元二次方程.
ax2+bx +c = 0(a , b , c为常数, a≠0)
ax2 称为二次项, a 称为二次项系数. bx 称为一次项,b 称为一次项系数. c 称为常数项.
一元二次方程的一般形式是
想一想 为什么一般形式中ax2+bx+c=0要限制a≠0，b、c 可以为零吗？
当 a ≠ 0 ， b = 0时 ，
当 a ≠ 0 ， c = 0时 ，
ax2＋bx = 0
当 a ≠ 0 ，b = c =0时 ，
总结：只要满足a ≠ 0 ，b ， c 可以为任意实数.
化简整理成x2-3x+2=0
判断下列方程是否为一元二次方程？
(2) x3+ x2=36
(1) x2+ x=36
例2:a为何值时，下列方程为一元二次方程？
(1)ax2－x=2x2
(2) (a－1)x |a|+1 －2x－7=0.
解：(1)将方程式转化为一般形式，得(a-2)x2-x=0,所以当a-2≠0，即a≠2时，原方程是一元二次方程； (2)由∣a ∣+1 =2，且a-1 ≠0知，当a=-1时，原方程是一元二次方程.
方法点拨：用一元二次方程的定义求字母的值的方法：根据未知数的最高次数等于2，列出关于某个字母的方程，再排除使二次项系数等于0的字母的值．
变式：方程(2a-4)x2－2bx+a=0, （1）在什么条件下此方程为一元二次方程？（2）在什么条件下此方程为一元一次方程？
解（1）当 2a－4≠0，即a ≠2 时是一元二次方程
（2）当a=2 且 b ≠0 时是一元一次方程
思考：一元一次方程与一元二次方程有什么区别与联系？
ax=b (a≠0）
ax2+bx+c=0 (a≠0）
整式方程，只含有一个未知数
例3：将方程3x(x-1)=5(x+2)化为一般形式，并分别指出它们的二次项、一次项和常数项及它们的系数.
3x2-3x=5x+10.
移项、合并同类项，得一元二次方程的一般形式
3x2-8x-10=0.
其中二次项是3x2,系数是3；一次项是-8x,系数是-8；常数项是-10.
视频：一元二次方程一般式
1. 下列哪些是一元二次方程？
(x+3)(2x-4)=x2
3y2=(3y+1)(y-2)
3.关于x的方程(k2－1)x2 ＋ 2 (k－1) x ＋ 2k ＋ 2＝0,当k 　　　时，是一元二次方程．当k 　　　时，是一元一次方程．
4.(1) 如图，已知一矩形的长为200cm,宽150cm.现在矩形中挖去一个圆，使剩余部分的面积为原矩形面积的四分之三.求挖去的圆的半径xcm应满足的方程（其中π取3）.
解：设由于圆的半径为xcm，则它的面积为 3x2 cm2.
(2) 如图，据某市交通部门统计，前年该市汽车拥有量为75万辆，两年后增加到108万辆.求该市两年来汽车拥有量的年平均增长率x应满足的方程.
解：该市两年来汽车拥有量的年平均增长率为x