





人教版九年级下册26.1.2 反比例函数的图象和性质备课课件ppt
展开2.掌握反比例函数的图象和性质,并会用性质解决问题.
1.能用描点法画出反比例函数的图象.
1.什么是反比例函数?其自变量的取值范围是什么,你能说明为什么吗?2.试举出几个反比例函数的例子.
3.一次函数的图象是什么?它有什么性质?反比例函数的图象又是什么?它又有什么性质呢?
画函数图象的一般步骤是什么?
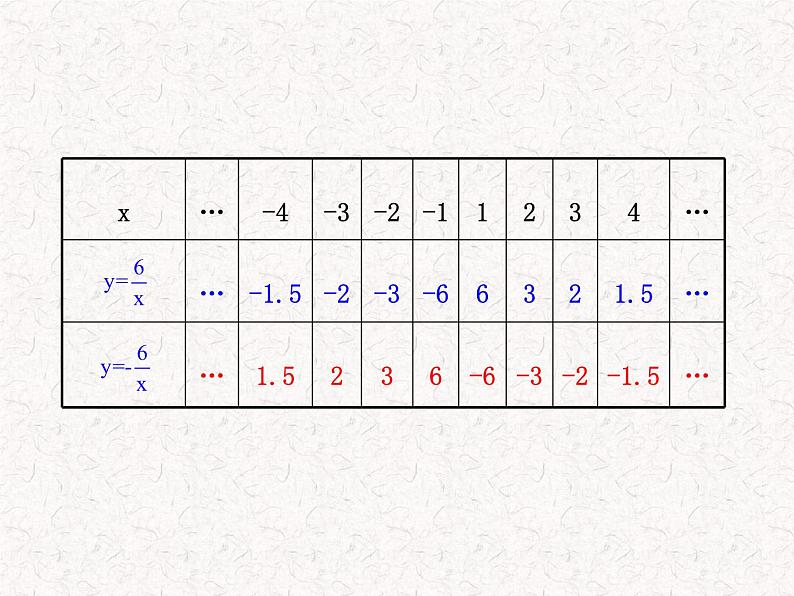
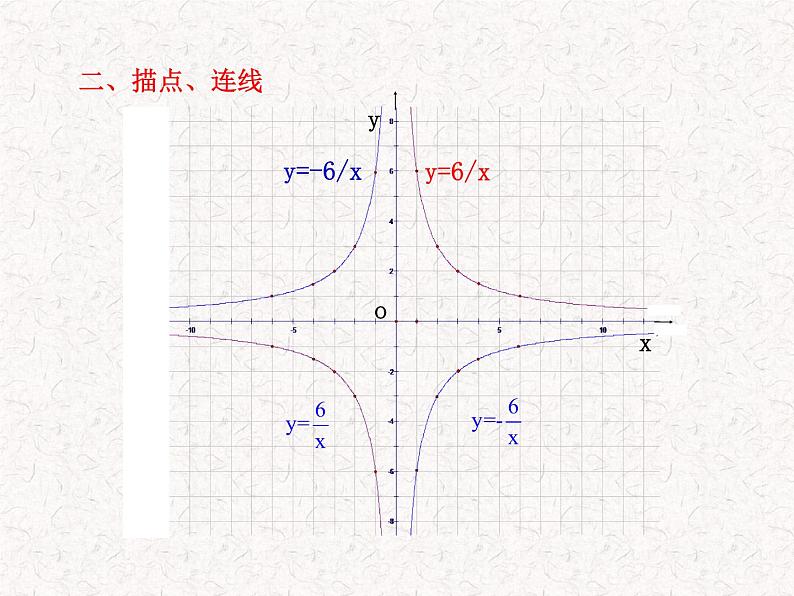
列表、 描点、 连线.
【例】画出反比例函数 和 的图象.
注意:①列表时自变量取值要均匀和对称②x≠0③选整数较好计算和描点.
1.反比例函数的图象是双曲线.2.当k>0时,图象的两个分支分布在第一、三象限内;在每个象限内y随x的增大而减小.3.当k<0时,图象的两个分支分布在第二、四象限内;在每个象限内y随x的增大而增大.(口诀:k大一三减,k小二四增)4.反比例函数图象关于原点对称,且关于直线y=x和y=-x对称.
y=kx ( k≠0 )
每个象限内, y随x的增大而减小
每个象限内, y随x的增大而增大
1.(上海·中考)在平面直角坐标系中,反比例函数图象的两支分别在( )(A)第一、三象限 (B)第二、四象限(C)第一、二象限 (D)第三、四象限【解析】选B.因为k<0,所以图象的两支分别在第二、四象限.
1.(凉山·中考)已知函数y=(m+1) 是反比例函数,且图象在第二、四象限内,则m的值是( )(A)2 (B)-2 (C)±2 (D)【解析】选B.由题意得:解得m=-2.
2.(绍兴·中考)已知(x1,y1),(x2,y2),(x3,y3)是反比例函数 的图象上的三个点,且x1<x2<0,x3>0,则y1,y2,y3的大小关系是( )(A)y3<y1<y2 (B)y2<y1<y3(C)y1<y2<y3 (D)y3<y2<y1【解析】选A.由反比例函数的性质可得,反比例函数 的图象在二,四象限,在第二象限y随x的增大而增大,且y>0,所以y1<y2.在第四象限y<0所以y3<y1<y2.
3.(杭州·中考) 如图,函数和函数的图象交于点M(2,m),N(-1,n),若y1>y2,则x的取值范围是( )
【解析】选D.由函数图象可知,当 时,一次函数图象在反比例函数图象的上方,即y1>y2 ,而当 时,一次函数图象在反比例函数图象的下方,即y1
5.已知反比例函数 的图象在第一、三象限,反比例函数 在x>0时,y随x的增大而增大,则k的取值范围是_______.【解析】∵ 的图象在第一、三象限, ∴2k+4>0.由于 在x>0时,y随x的增大而增大,∴k-3<0.综上,k需满足 解得:-2<k<3.答案:-2<k<3
6.设函数y=(m-2)xm-4.当m取何值时,它是反比例函数?它的图象位于哪些象限内?在每个象限内,当x的值增大时,对应的y值是随着增大,还是随着减小?
【解析】依题意,得 解得m=3,当m=3时,原函数是反比例函数,即 它的图象在第一、三象限内.由m-2=3-2>0知,在每个象限内,当x的值增大时,对应的y值随着减小.
初中数学人教版九年级下册26.1.2 反比例函数的图象和性质评课ppt课件: 这是一份初中数学人教版九年级下册26.1.2 反比例函数的图象和性质评课ppt课件,共23页。PPT课件主要包含了应用新知,巩固新知,课堂小结,布置作业,创设情境,探究新知,反比例函数,下列反比例函数,数形结合,如何求这个量等内容,欢迎下载使用。
数学九年级下册第二十六章 反比例函数26.1 反比例函数26.1.2 反比例函数的图象和性质教学课件ppt: 这是一份数学九年级下册第二十六章 反比例函数26.1 反比例函数26.1.2 反比例函数的图象和性质教学课件ppt,共46页。PPT课件主要包含了复习引入,问题1,问题2,典例精析,练一练,合作探究,S1S2,S1S2k,S1S2-k,做一做等内容,欢迎下载使用。
初中人教版26.1.2 反比例函数的图象和性质集体备课ppt课件: 这是一份初中人教版26.1.2 反比例函数的图象和性质集体备课ppt课件,共39页。













