数学九年级下册28.1 锐角三角函数图片课件ppt

这是一份数学九年级下册28.1 锐角三角函数图片课件ppt，共14页。PPT课件主要包含了特殊角的正弦函数值，有什么关系，角A的对边，角A的邻边等内容，欢迎下载使用。

1、理解余弦、正切的概念；2、培养学生观察、比较、分析、概括的思维能力.
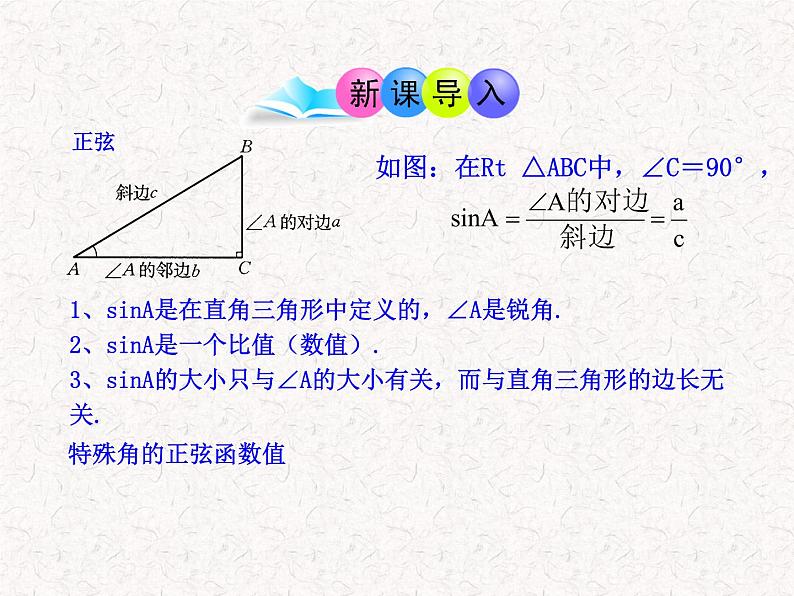
1、sinA是在直角三角形中定义的，∠A是锐角.2、sinA是一个比值（数值）.3、sinA的大小只与∠A的大小有关，而与直角三角形的边长无关.
如图：在Rt △ABC中，∠C＝90°，
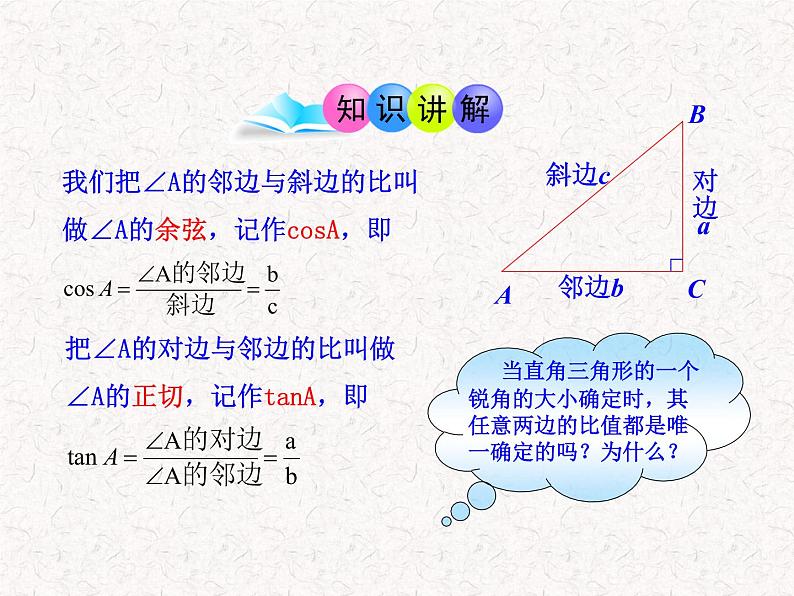
当直角三角形的一个锐角的大小确定时，其任意两边的比值都是唯一确定的吗？为什么？
我们把∠A的邻边与斜边的比叫做∠A的余弦，记作csA，即
把∠A的对边与邻边的比叫做∠A的正切，记作tanA，即
在直角三角形中，当锐角A的度数一定时，不管三角形的大小如何，∠A的 对边与斜边的比及对边与邻边的比是一个固定值.
任意画Rt△ABC和Rt△A′B′C′，使得∠C=∠C′=90°，∠A=∠A′=α.那么
由于∠C=∠C′=90°，∠A=∠A′=α，所以Rt△ABC∽Rt△A′B′C′，
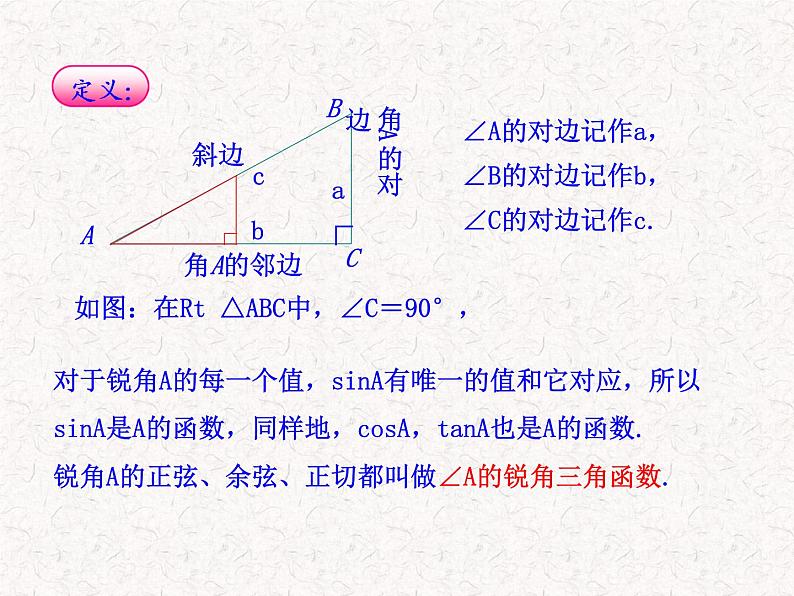
∠A的对边记作a，∠B的对边记作b，∠C的对边记作c.
对于锐角A的每一个值，sinA有唯一的值和它对应，所以sinA是A的函数，同样地，csA，tanA也是A的函数.
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
【例】如图，在Rt△ABC中，∠C=90°，BC=6，sinA= ，求csA，tanB的值.
1、如图,在Rt△ABC中,锐角A的邻边和斜边同时扩大100倍,tanA的值（ ）A.扩大100倍 B.缩小100倍 C.不变 D.不能确定
2、下图中∠ACB=90°，CD⊥AB,垂足为D.指出∠A和∠B的对边、邻边.
1.（湖州中考）如图，已知在Rt△ABC中，∠C=90°，BC=1，AC=2，则tanA的值为( )A.2 B． C． D．【解析】选B.根据正切的函数定义，角A的正切应是它的对边与邻边的比，所以B是正确，A是∠B的正切；C和D都错．
2.（黄冈中考）在△ABC中，∠C＝90°，sinA＝则tanB＝（ ）
3.（丹东中考）如图，小颖利用有一个锐角是30°的三角板测量一棵树的高度，已知她与树之间的水平距离BE为5m，AB为1.5m（即小颖的眼睛距地面的距离），那么这棵树高是（ ）
4．（怀化中考）在Rt△ABC中，∠C=90°，sinA=则csB的值等于（ ）
5.（东阳中考）如图，为了测量河两岸A.B两点的距离，在与AB垂直的方向点C处测得AC＝a，∠ACB＝α，那么AB等于（ ）A.a·sinα B.a·tanα C.a·csα D.
【解析】选B.在Rt△ABC中，tanα=
所以AB=a·tanα
【规律方法】 1.sinA,csA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)；2.sinA,csA是一个完整的符号,表示∠A的正弦、余弦,习惯省去“∠”符号；3.sinA,csA的大小只与∠A的大小有关,而与直角三角形的边长无关.