初中数学人教版八年级上册第十一章 三角形综合与测试随堂练习题

这是一份初中数学人教版八年级上册第十一章 三角形综合与测试随堂练习题，共15页。试卷主要包含了7条长度均为整数厘米的线段，下列关于三角形分类不正确的是等内容，欢迎下载使用。




一．选择题（共12小题）


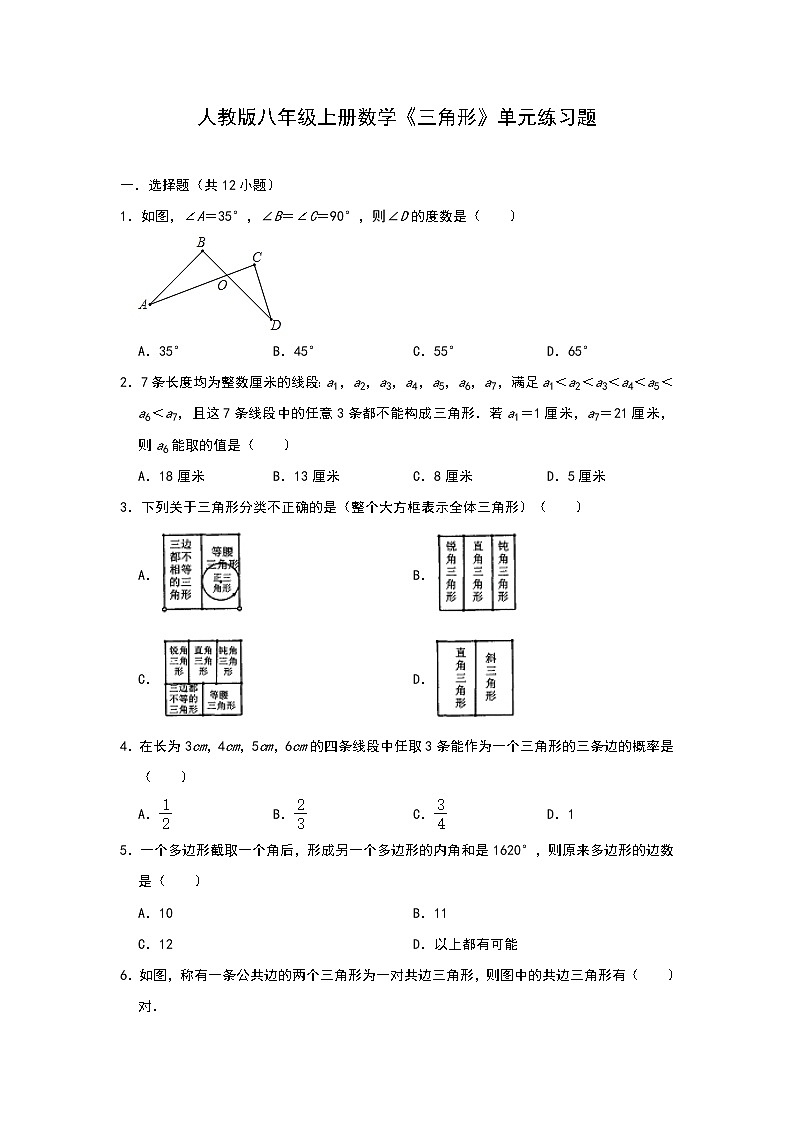
1．如图，∠A＝35°，∠B＝∠C＝90°，则∠D的度数是（ ）





A．35°B．45°C．55°D．65°


2．7条长度均为整数厘米的线段：a1，a2，a3，a4，a5，a6，a7，满足a1＜a2＜a3＜a4＜a5＜a6＜a7，且这7条线段中的任意3条都不能构成三角形．若a1＝1厘米，a7＝21厘米，则a6能取的值是（ ）


A．18厘米B．13厘米C．8厘米D．5厘米


3．下列关于三角形分类不正确的是（整个大方框表示全体三角形）（ ）


A．B．


C．D．


4．在长为3cm，4cm，5cm，6cm的四条线段中任取3条能作为一个三角形的三条边的概率是（ ）


A．B．C．D．1


5．一个多边形截取一个角后，形成另一个多边形的内角和是1620°，则原来多边形的边数是（ ）


A．10B．11


C．12D．以上都有可能


6．如图，称有一条公共边的两个三角形为一对共边三角形，则图中的共边三角形有（ ）对．





A．8B．16C．24D．32


7．已知正六边形的半径为2，则这个正六边形的面积是（ ）


A．6B．12C．D．


8．如图，在△ABC中，∠A＝60度，点D，E分别在AB，AC上，则∠1+∠2的大小为多少度（ ）





A．140B．190C．320D．240


9．把一个多边形纸片沿一条直线截下一个三角形后，变成一个18边形，则原多边形纸片的边数不可能是（ ）


A．16B．17C．18D．19


10．如图，△ABC绕点C按顺时针方向旋转57°后得到△DEC，如果DC⊥BC，那么∠A+∠B等于（ ）





A．147°B．90°C．157°D．57°


11．如图，若干全等正五边形排成环状．图中所示的是前3个五边形，要完成这一圆环还需（ ）个五边形．





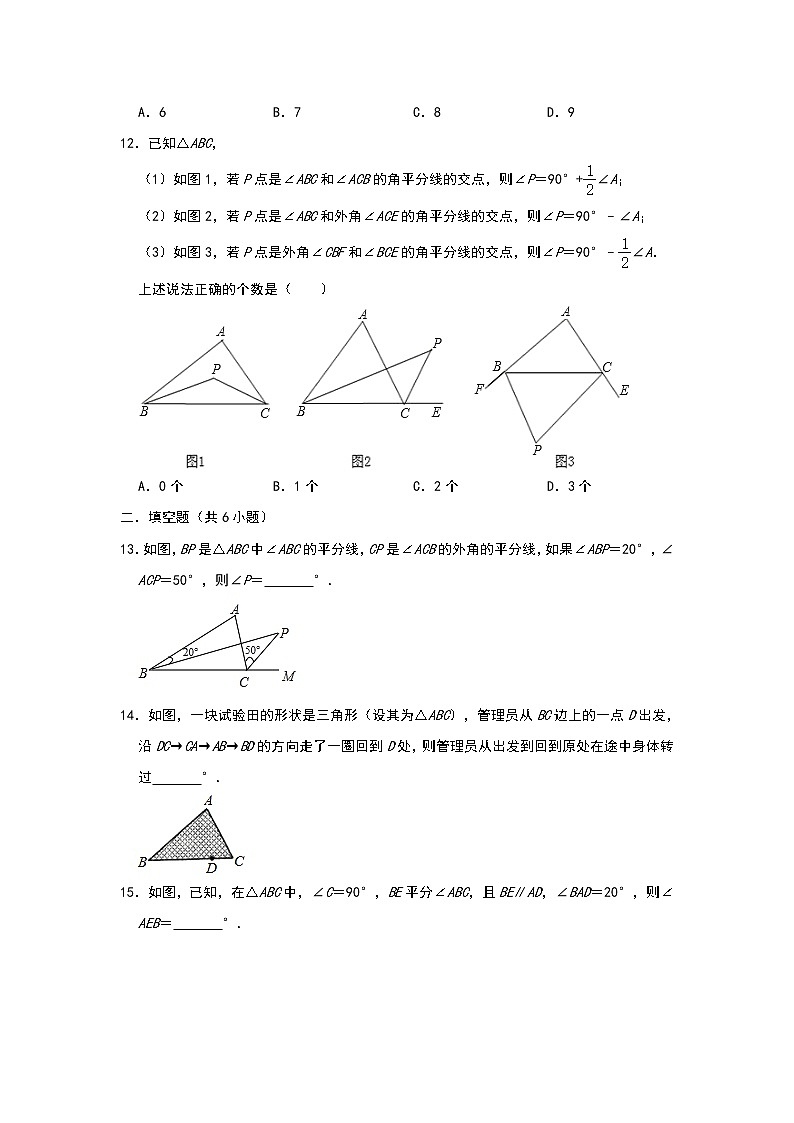
A．6B．7C．8D．9


12．已知△ABC，


（1）如图1，若P点是∠ABC和∠ACB的角平分线的交点，则∠P＝90°+∠A；


（2）如图2，若P点是∠ABC和外角∠ACE的角平分线的交点，则∠P＝90°﹣∠A；


（3）如图3，若P点是外角∠CBF和∠BCE的角平分线的交点，则∠P＝90°﹣∠A．


上述说法正确的个数是（ ）





A．0个B．1个C．2个D．3个


二．填空题（共6小题）


13．如图，BP是△ABC中∠ABC的平分线，CP是∠ACB的外角的平分线，如果∠ABP＝20°，∠ACP＝50°，则∠P＝ °．





14．如图，一块试验田的形状是三角形（设其为△ABC），管理员从BC边上的一点D出发，沿DC→CA→AB→BD的方向走了一圈回到D处，则管理员从出发到回到原处在途中身体转过 °．





15．如图，已知，在△ABC中，∠C＝90°，BE平分∠ABC，且BE∥AD，∠BAD＝20°，则∠AEB＝ °．





16．如图，在△ABC中，点D是BC上一点，∠BAD＝80°，AB＝AD＝DC，则∠C＝ 度．





17．一个机器人从点O出发，每前进1米，就向右转体a°（1＜a＜180），照这样走下去，如果他恰好能回到O点，且所走过的路程最短，则a的值等于 ．


18．如图所示，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第n个图形需要黑色棋子的个数是 ．





三．解答题（共6小题）


19．如图，在△ABC中，∠BAC＝90°，AD⊥BC于点D，AE平分∠DAC，∠B＝50°，


求∠BAD和∠AEC的度数．





20．如图：在直角坐标系中，已知B（b，0），C（0，c），且|b+3|+（2c﹣8）2＝0．


（1）求B、C的坐标；


（2）点A、D是第二象限内的点，点M、N分别是x轴和y轴负半轴上的点，∠ABM＝∠CBO，CD∥AB，MC、NB所在直线分别交AB、CD于E、F，若∠MEA＝70°，∠CFB＝30°．求∠CMB﹣∠CNB的值；


（3）如图：AB∥CD，Q是CD上一动点，CP平分∠DCB，BQ与CP交于点P，给出下列两个结论：①的值不变；②的值改变．其中有且只有一个是正确的，请你找出这个正确的结论并求其定值．





21．观察以下图形，回答问题：





（1）图②有 个三角形；图③有 个三角形；图④有 个三角形；…猜测第七个图形中共有 个三角形．


（2）按上面的方法继续下去，第n个图形中有 个三角形（用n的代数式表示结论）．


22．如图，在四边形ABCD中，AB∥CD，对角线AC与BD相交于点E，且∠DAC＝∠DCA．


（1）求证：AC平分∠BAD；


（2）若∠AEB＝125°，且∠ABD＝2∠CBD，DF平分∠ADB交AB边于点F，求∠BDF﹣∠CBD的值．





23．（1）我们知道“三角形三个内角的和为180°”．现在我们用平行线的性质来证明这个结论是正确的．


已知：∠BAC、∠B、∠C是△ABC的三个内角，如图1


求证：∠BAC+∠B+∠C＝180°


证明：过点A作直线DE∥BC（请你把证明过程补充完整）


（2）请你用（1）中的结论解答下面问题：


如图2，已知四边形ABCD，求∠A+∠B+∠C+∠D的度数．





24．如图①，∠1、∠2是四边形ABCD的两个不相邻的外角．


（1）猜想并说明∠1+∠2与∠A、∠C的数量关系；


（2）如图②，在四边形ABCD中，∠ABC与∠ADC的平分线交于点O．若∠A＝50°，∠C＝150°，求∠BOD的度数；


（3）如图③，BO、DO分别是四边形ABCD外角∠CBE、∠CDF的角平分线．请直接写出∠A、∠C与∠O的数量关系 ．








参考答案


一．选择题


1．解：∵∠B＝∠C＝90°，∠AOB＝∠COD，


∴∠D＝∠A＝35°．


故选：A．


2．解：若a1＝1厘米，则后边的一个一定大于或等于前边的两个的和，则一定有：a2＝2，a3＝3，a4＝5，a5＝8，a6＝13，a7＝21，


故选：B．


3．解：根据选项，可知根据角和边来对三角形分别进行分类．


故选：C．


4．解：任取3条能作为一个三角形的三条边是一个必然事件，概率是1．故选D．


5．解：∵内角和是1620°的多边形是边形，


又∵多边形截去一个角有三种情况．一种是从两个角的顶点截取，这样就少了一条边，即原多边形为12边形；


另一种是从两个边的任意位置截，那样就多了一条边，即原多边形为10边形；


还有一种就是从一个边的任意位置和一个角顶点截，那样原多边形边数不变，还是11边形．


综上原来多边形的边数可能为10、11、12边形，


故选：D．


6．解：以AB为公共边的三角形有：△ABD和△ABC；


以AC为公共边的三角形有：△ACE和△ACB；


以AD为公共边的三角形有：△ADE和△ABD；


以AE为公共边的三角形有：△AED和△AEC；


以BC为公共边的三角形有：△BCO和△BCA和△BCD和△BCE，4个三角形中任何两个都是共边三角形，有6对；


以BD为公共边的三角形有：△BDC，△BDE，BDA任何两个都是3对共边三角形；


以BE为公共边的三角形有：△BEO，△BED，△BEC任何两个都是3对共边三角形．


以OB为公共边的三角形有：△OBE和△OBC；


以CD为公共边的三角形有：△CDO和△CDB和△CDE任何两个都是3对共边三角形．


以CE为公共边的三角形有：△CED，△CEA，△CEB任何两个都是3对共边三角形；


以CO为公共边的三角形有：△COD和△COB；


以DE为公共边的三角形有：△AED和△OED和△BED和三角CED，4个三角形中任何两个都是共边三角形，有6对；


以OD为公共边的三角形有：△ODC和△ODE；


以OE为公共边的三角形有：△OBE和△ODE．


共32对．


故选：D．


7．解：根据题意，正六边形的半径为2，


而正六边形可以分解为六个全等的三角形，如图


且每个三角形的边长都为2，


易得每个三角形的面积为，


故这个正六边形的面积是6．


故选：C．





8．解：∵∠A+∠ADE＝∠1，∠A+∠AED＝∠2，


∴∠A+（∠A+∠ADE+∠AED）＝∠1+∠2，


∵∠A+∠ADE+∠AED＝180°，∠A＝60°，


∴∠1+∠2＝60°+180°＝240°．


故选：D．


9．解：当剪去一个角后，剩下的部分是一个18边形，


则这张纸片原来的形状可能是18边形或17边形或19边形，不可能是16边形．


故选：A．


10．解：∵△ABC绕点C按顺时针方向旋转57°后得到△DEC，


∴∠BCA＝∠ECD，∠BCE＝57°


又∵DC⊥BC，


∴∠ECD＝90°﹣∠BCE＝90°﹣57°＝33°，


∴∠BCA＝∠ECD＝33°，


∴∠A+∠B＝180°﹣∠BCA＝180°﹣33°＝147°


故选：A．


11．解：五边形的内角和为（5﹣2）•180°＝540°，


所以正五边形的每一个内角为540°÷5＝108°，


如图，延长正五边形的两边相交于点O，则∠1＝360°﹣108°×3＝360°﹣324°＝36°，


360°÷36°＝10，


∵已经有3个五边形，


∴10﹣3＝7，


即完成这一圆环还需7个五边形．


故选：B．





12．解：（1）若P点是∠ABC和∠ACB的角平分线的交点，


则∠PBC＝∠ABC，∠PCB＝∠ACB


则∠PBC+∠PCB＝（∠ABC+∠ACB）＝（180°﹣∠A）


在△BCP中利用内角和定理得到：


∠P＝180﹣（∠PBC+∠PCB）＝180﹣（180°﹣∠A）＝90°+∠A，


故成立；


（2）当△ABC是等腰直角三角形，∠A＝90°时，结论不成立；


（3）若P点是外角∠CBF和∠BCE的角平分线的交点，


则∠PBC＝∠FBC＝（180°﹣∠ABC）＝90°﹣∠ABC，


∠BCP＝∠BCE＝90°﹣∠ACB


∴∠PBC+∠BCP＝180°﹣（∠ABC+∠ACB）


又∵∠ABC+∠ACB＝180°﹣∠A


∴∠PBC+∠BCP＝90°+∠A，


在△BCP中利用内角和定理得到：


∠P＝180﹣（∠PBC+∠PCB）＝180﹣（180°+∠A）＝90°﹣∠A，


故成立．


∴说法正确的个数是2个．


故选：C．


二．填空题（共6小题）


13．解：∵BP是△ABC中∠ABC的平分线，CP是∠ACB的外角的平分线，


∴∠ABP＝∠CBP＝20°，∠ACP＝∠MCP＝50°，


∵∠PCM是△BCP的外角，


∴∠P＝∠PCM﹣∠CBP＝50°﹣20°＝30°，


故答案为：30°．


14．解：∵管理员走过一圈正好是三角形的外角和，


∴从出发到回到原处在途中身体转过360°．


故答案为：360．


15．解：∵BE∥AD，


∴∠ABE＝∠BAD＝20°，


∵BE平分∠ABC，


∴∠EBC＝∠ABE＝20°，


∵∠C＝90°，


∴∠BEC＝70°，


∴∠AEB＝110°，


故答案为：110．


16．解：∵∠BAD＝80°，AB＝AD＝DC，


∴∠ABD＝∠ADB＝50°，


由三角形外角与外角性质可得∠ADC＝180°﹣∠ADB＝130°，


又∵AD＝DC，


∴∠C＝∠DAC＝（180°﹣∠ADC）＝25°，


∴∠C＝25°．


17．解：根据题意，机器人所走过的路线是正多边形，


∴边数n＝360°÷a°，


走过的路程最短，则n最小，a最大，


n最小是3，a°最大是120°．


故答案为：120．


18．解：第一个是1×3，


第二个是2×4，


第三个是3×5，


…


第 n个是n•（n+2）＝n2+2n


故答案为：n2+2n．


三．解答题（共6小题）


19．解：在△ABC中，


∵∠BAC＝90°，∠B＝50°，


∴∠C＝90°﹣∠B＝40°，


∵AD⊥BC于点D，


∴∠BAD＝90°﹣∠B＝40°；


在△ADC中，


∵∠ADC＝90°，∠C＝40°，


∴∠DAC＝90°﹣∠C＝50°，


∵AE平分∠DAC，


∴∠DAE＝∠DAC＝25°，


在△DAE中，


∵∠ADE＝90°，∠DAE＝25°，


∴∠AED＝90°﹣∠DAE＝65°，


∴∠AEC＝180°﹣∠AED＝180°﹣65°＝115°．


20．解：（1）由题意得：b+3＝2c﹣8＝0，（1分）


∴b＝﹣3，c＝4．（2分）


∴B（﹣3，0），C（0，4）．（3分）





（2）∵CD∥AB，


∴∠DCB+∠ABC＝180°．


∵∠COB＝90°，


∴∠CBO+∠BCO＝90°．（4分）


∵（∠GCF+∠DCB+∠BCO）+（∠CBO+∠ABC+∠ABM）


＝180°+180°＝360°，


∴∠ABM+∠GCF＝360°﹣180°﹣90°＝90°．（5分）


又∵∠CMB＝∠MEA﹣∠ABM＝70°﹣∠ABM


∠CNB＝∠GCF﹣∠CFB＝∠GCF﹣30°（6分）


∴∠CMB﹣∠CNB＝（70°﹣∠ABM）﹣（∠GCF﹣30°）


＝100°﹣（∠ABM+∠GCF）


＝100°﹣90°


＝10°．





（3）答：①的值不变，定值为2．


∵CP平分∠DCB，


∴∠QCB＝2∠PCB．


又∵∠DQB＝∠QBC+∠QCB，


∴∠DQB+∠QBC


＝（∠QBC+∠QCB）+∠QBC


＝2∠QBC+2∠PCB


＝2（∠QBC+∠PCB）


＝2∠QPC


∴②＝＝2．（12分）








21．解：（1）图②有3个三角形；图③有5个三角形；图④有7个三角形；…猜测第七个图形中共有13个三角形．





（2）∵图②有3个三角形，3＝2×2﹣1；


图③有5个三角形，5＝2×3﹣1；


图④有7个三角形，7＝2×4﹣1；





∴第n个图形中有（2n﹣1）个三角形．


故答案为3，5，7，13，（2n﹣1）．


22．解：（1）证明：∵AB∥CD，


∴∠BAC＝∠DCA，


又∵∠DAC＝∠DCA，


∴∠BAC＝∠DAC，


∴AC平分∠BAD；





（2）∵∠BAC＝∠DAC，∠DAC+∠ADB＝∠AEB＝125°，


∴∠ADB＝125°﹣∠BAC，


又∵DF平分∠ADB交AB边于点F，


∴∠BDF＝，


由∠AEB＝125°可得∠BAC＝55°﹣∠ABD，


∵∠ABD＝2∠CBD，


∴∠BAC＝55°﹣2∠CBD，


∴，


∴∠BDF﹣∠CBD＝＝35°．


23．解：（1）证明：过点A作直线DE∥BC，


∴∠B＝∠BAD，∠C＝∠CAE（两直线平行，内错角相等），


∵∠BAD+∠BAC+∠CAE＝180°，


∴∠B+∠BAC+∠C＝180°；





（2）连接BD，





由（1）可知∠A+∠ABD+∠ADB＝180°，∠C+∠BDC+∠CBD＝180°，


∴∠A+∠ABC+∠C+∠ADC＝360°．


24．解：（1）猜想：∠1+∠2＝∠A+∠C，


∵∠1+∠ABC+∠2+∠ADC＝360°，


又∵∠A+∠ABC+∠C+∠ADC＝360°，


∴∠1+∠2＝∠A+∠C；


（2）∵∠A＝50°，∠C＝150°，


∴∠ABC+∠ADC＝360°﹣200°＝160°，


又∵BO、DO分别平分∠ABC与∠ADC，


∴∠OBC＝∠ABC，∠ODC＝∠ADC，


∴∠OBC+∠ODC＝（∠ABC+∠ADC）＝80°，


∴∠BOD＝360°﹣（∠OBC+∠ODC+∠C）＝130°；


（3）∠A、∠C与∠O的数量关系为为：


∠C﹣∠A＝2∠O．


理由如下：


∵BO、DO分别是四边形ABCD外角∠CBE、∠CDF的角平分线．


∴∠FDC＝2∠FDO＝2∠ODC，∠EBC＝2∠EBO＝2∠CBO，


由（1）可知：


∠FDO+∠EBO＝∠A+∠O，


2∠FDO+2∠EBO＝∠A+∠C，


∴2∠A+2∠O＝∠A+∠C，


∴∠C﹣∠A＝2∠O．


故答案为：∠C﹣∠A＝2∠O．