高中1 生活中的变量关系导学案

这是一份高中1 生活中的变量关系导学案，共15页。学案主要包含了教学目标，知识清单，基础过关，经典例题，课堂达标，能力提升，参考答案等内容，欢迎下载使用。

【教学目标】


重点、难点


1、了解两个变量之间的几种关系；（重点）


2、区分变量之间是函数关系还是依赖关系。（难点）


学科素养


通过对两个变量之间关系的判断，发展学生的思维能力；


【知识清单】


1. 对于一个变量的每一个值，另一个变量都有唯一确定的值与之对应，才称它们之间有__________。


2. 构成函数关系的两个变量，必须是对于自变量的每一个值，因变量都有_________值与之对应。


【基础过关】


1．在一次实验中，马达同学把一根弹簧的上端固定、在其下端悬挂物体，下面是测得的弹簧的长度y与所挂物体质量x的一组对应值．


（1）上表反映了哪两个变量之间的关系， 是自变量， 是因变量．


（2）弹簧长度y与所挂物体质量x之间的关系可以用式子表示为：_________．








2.一支原长为20cm的蜡烛，点燃后，其剩余长度y（cm）与燃烧时间x（min）之前的关系如表：


（1）表中反映的自变量是什么？因变量是什么？


（2）求出剩余长度y（cm）与燃烧时间x（min）之间的关系式；








【经典例题】


例1.下列过程中变量之间是否存在依赖关系,其中哪些是函数关系:


(1)地球绕太阳公转的过程中,二者的距离与时间的关系;


(2)在空中作斜抛运动的铅球,铅球距地面的高度与时间的关系;


(3)某水文观测点记录的水位与时间的关系;


(4)某十字路口,通过汽车的数量与时间的关系;











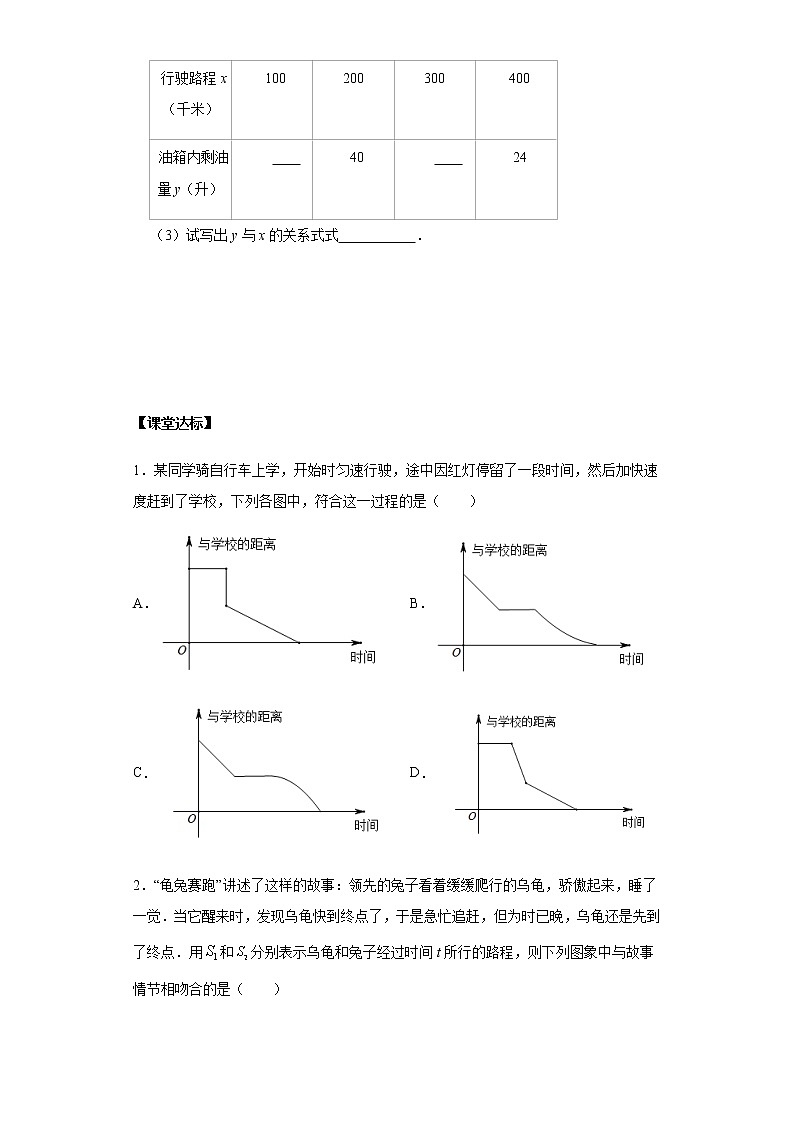
例2．一辆汽车油箱内有油56升，从某地出发，每行驶1千米，耗油0.08升，如果设油箱内剩油量为y（升），行驶路程为x（千米），则y随x的变化而变化


（1）在上述变化过程中，自变量是 ；因变量是 ．


（2）用表格表示汽车从出发地行驶100千米、200千米、300千米、400千米时的剩油量．


请将表格补充完整：


（3）试写出y与x的关系式式 ．














【课堂达标】


1．某同学骑自行车上学，开始时匀速行驶，途中因红灯停留了一段时间，然后加快速度赶到了学校，下列各图中，符合这一过程的是（ ）


A．B．


C．D．


2．“龟兔赛跑”讲述了这样的故事：领先的兔子看着缓缓爬行的乌龟，骄傲起来，睡了一觉．当它醒来时，发现乌龟快到终点了，于是急忙追赶，但为时已晚，乌龟还是先到了终点．用和分别表示乌龟和兔子经过时间t所行的路程，则下列图象中与故事情节相吻合的是（ ）


A．B．


C．D．


3.在一次实验中，马达同学把一根弹簧的上端固定、在其下端悬挂物体，下面是测得的弹簧的长度y与所挂物体质量x的一组对应值．


（1）上表反映了哪两个变量之间的关系，_____是自变量，_____是因变量．


（2）当所挂物体重量为3千克时，弹簧长_____；不挂重物时弹簧长_____．


（3）弹簧长度y与所挂物体质量x之间的关系可以用式子表示为：_____．


4.有研究表明，声音在空气中的传播速度与空气的温度有关，当空气的温度变化，声音的传播速度也将随着变化．声音在空气中传播速度与空气温度关系一些数据（如下表格）


（1）指出在这个变化过程中的自变量和因变量；


（2）当声音在空气中传播速度为342m/s时，此时空气的温度是多少？


（3）该数据表明：空气的温度每升高，声音的传播速度将增大（或减少）多少？


（4）用表示声音在空气中的传播速度，表示空气温度，根据（3）中你发现的规律，直接写出与之间的关系式．














【能力提升】


1.向高为H的水瓶中注水，注满为止．如果注水量V与水深h的函数关系的图象如图所示，那么水瓶的形状是 （ ）





A．B．


C．D．


2．一辆汽车在公路上正常行驶，其中有这样一些量：①行驶的速度；②汽车的重量；③车上乘坐的人数；④行驶的时间. 其中有函数的对应关系的两个量是（ ）


A．与B．与C．与D．与


3．“距离地面越高，温度越低”，下表反映了距离地面高度与温度之间的变化关系：


（1）上表反映的变化关系中， 是自变量， 是因变量；


（2）如果用h表示距离地面的高度，用t表示温度，那么用h表示t的关系式是 ；


（3）你能猜出距离地面7千米的高空温度是多少吗？


4．某桶装水经营部每天的房租､工人工资等固定支出为200元，每桶水的成本价为5元，销售单价与每日销售量的关系如下表，根据表中的数据，回答下列问题：


（1）销售单价与每日销售量之间有什么关系？


（2）单价确定为多少时？可以获得最大利润，并求出最大利润.




















5．如图所示，是某辆汽车的行驶情况记录，根据图中数据回答下列问题.





（1）汽车从开始行驶到最后停止共行驶了多少分钟？期间的最大速度是多少？汽车有几个时间点的时速为20千米/小时？


（2）写出汽车出发10分钟到18分钟之间速度(千米/小时)与时间(分钟)的函数关系式，并算出这段时间中，在多少分钟时的速度为20千米/小时.


【参考答案】


【知识清单】


1. 依赖关系 2.唯一确定的


【基础过关】


1.所挂物体的质量，弹簧的长度；y＝2x+18（x≥0）


2.（1）表中反映的自变量是燃烧时间，因变量是剩余长度；


（2）由表可知燃烧时间每增加10min，长度减小1cm，


∴y＝20﹣；


【经典例题】


1.（1）依赖关系 (2) 函数关系C (3) 函数关系 (4) 函数关系


2. 解：（1）在上述变化过程中，自变量是汽车行驶路程；因变量是邮箱内剩油量，


故答案为：汽车行驶路程，邮箱内剩油量；


（2）56﹣0.08×100＝48，56﹣0.08×300＝32，





（3）y与x的关系式式是y＝56﹣0.08x，


[课堂达标]


1．C


【解析】


【分析】


第一段匀速慢，第二段停止，第三段加速，得出与学校的距离的变化情况，即可得出结论.


【详解】


由于开始匀速行驶，所以离学校的距离匀速减少，


中间一段停留，与学校距离没变，然后加速赶到学校，


与学校的距离在同样的时间段内减少的越来越快，


故选：C.


【点睛】


本题考查函数的图象以及函数的实际应用，属于基础题.


2．D


【解析】


【分析】


分别分析乌龟和兔子随时间变化它们的路程变化情况,即直线的斜率变化即可.


【详解】


对于乌龟,其运动过程分为两段:从起点到终点乌龟没有停歇,一直以匀速前进,其路程不断增加;到终点等待兔子那段时间路程不变,此时图象为水平线段;


对于兔子，其运动过程分三段:开始跑的快,即速度大,所以路程增加的快;中间由于睡觉,速度为零,其路程不变;醒来时追赶乌龟,速度变大,所以路程增加的快;


但是最终是乌龟到达终点用的时间短.


故选:D


【点睛】


本题考查直线斜率的意义;属于基础题.


3.答案：所挂物体的质量 弹簧的长度 24cm 18cm y＝2x+18（x≥0）


【解析】


【分析】


根据变量的概念和表中的数据可直接得到答案.


【详解】


（1）上表反映了弹簧长度与所挂物体质量之间的关系；其中所挂物体质量是自变量，弹簧长度是因变量；


（2）当所挂物体重量为3千克时，弹簧长24厘米；当不挂重物时，弹簧长18厘米；


（3）弹簧长度y与所挂物体质量x之间的关系可以用式子表示为：．


【点睛】


本题考查的是生活中的变量关系，较简单.


4.（1）自变量是温度，因变量是声速；（2）；（3）；（4）．


【解析】


【分析】


（1）由题设关于变量的表述可得温度为自变量，声速为因变量；


（2）根据表中数据可得传播速度为342m/s时，空气的温度为；


（3）根据数据表中的数据可得声音的传播速度将增大；


（4）根据散点图可得出与之间的关系为，代入表中两组数据后可求函数关系式.


【详解】


（1）由题设可得：当空气的温度变化，声音的传播速度也将随着变化．


因此自变量是温度，因变量是声速.


（2）根据题设中给出的数据表可知：当传播速度为342m/s时，空气的温度为.


（3）因为，


所以空气的温度每升高，声音的传播速度将增大.


（4）数据表对应的散点图如图所示：





故与之间的关系为，所以，解得，


所以.


【点睛】


本题考查根据数据寻找拟合函数，还考查了对数据的分析与整理，注意函数形式的确定应依据散点图的形状来确定，本题属于基础题.


【能力提升】


1．B


【解析】


试题分析：取，由图象可知，此时注水量大于容器容积的，故选B.


考点：函数图像．


2．A


【解析】


【分析】


由公路上行驶的汽车，每个行驶的时间，都有唯一的速度对应，结合函数的概念，即可求解.


【详解】


由题意，公路上行驶的汽车，每个行驶的时间，都有唯一的速度，


所以两个变量“时间”与“速度”之间是函数关系.


故选：A.


【点睛】


本题主要考查了函数概念及其应用，其中解答中熟记函数的基本概念，合理判定是解答的关键，着重考查分析问题和解答问题的能力，属于基础题.


3．（1）距离地面的高度，温度；（2）t＝﹣6h+20；（3）﹣22℃


【解析】


【分析】


（1）由于温度是随高度的变化而变化的，所以自变量是距离地面的高度，因变量是温度，


（2）由表中的数据可知，高度每增加1千米，温度降低6℃，所以两个变量之间是一次函数的关系，所以利用待定系数法求解函数关系式；


（3）直接用（2）中得到的关系式求解


【详解】


（1）由图可知，


表中自变量是距离地面的高度，因变量是温度，


（2）设t＝kh+b，


则， 得，


即h与t关系是：t＝﹣6h+20；


（3）当h＝7时，t＝﹣6×7+20＝﹣22（℃）．


所以距离地面7千米的高空温度是﹣22℃


【点睛】


此题考查了两变量间的关系，属于基础题.


4．（1）随着单价的提高，日销售量在减少，销售单价每提高1元，日销售量减少40桶，销售单价与日销售量之间为函数关系；（2）单价确定为11.5元，获得最大利润为1490元.


【解析】


【分析】


（1）由销售单价与日销售量的表格可知，销售单价与日销量成函数关系；


（2）先求解出日销售量与销售单价的函数关系式，再列出利润关于的解析式，然后确定利润最值及利润最大时销售单价的值.


【详解】


（1）随着单价的提高，日销售量在减少，销售单价每提高1元，日销售量减少40桶，销售单价与日销售量之间为函数关系；


（2）设销售单价为元，获得的利润为元.设日销售量满足：，


由图表可知，日销售量为：，解得，，


即，


根据题意得，


即


当时，


所以单价确定为11.5元，获得最大利润为1490元.


【点睛】


本题考查二次函数的实际应用问题，考查学生处理问题分析问题的能力，难度一般.解答时，关键在于列出利润关于销售单价的函数关系式，然后利用二次函数的性质求解最值.


5．（1）共行驶了22分钟，期间的最大速度为80千米/小时，有4个时间点车速为20千米/小时；（2）函数关系式，发12分钟时车速为20千米/小时.


【解析】


【分析】


（1）根据某辆汽车的行驶情况记录的函数图象，可得该汽车共行驶时间，以及最大速度和车速为20千米/小时的时间点，得到答案；


（2）在出发10分钟到18分钟这段时间中，设为，根据表中的数据列出方程组，即可求得速度与时间的函数关系式，进而得到答案.


【详解】


（1）根据某辆汽车的行驶情况记录的函数图象，可得该汽车共行驶了分钟，


期间的最大速度为80千米/小时，有4个时间点车速为20千米/小时；


（2）在出发10分钟到18分钟这段时间中，速度与时间是一次函数关系，


设为，


由图表中的数据，可得当时，，当时，，


代入得，解得，


所以速度(千米/小时)与时间(分钟)的函数关系式：，其中


当时，即，解得，即出发12分钟时车速为20千米/小时.


【点睛】


本题主要考查了一次函数的解析式的求解，以及函数的图象的识别与应用，着重考查数形结合思想，以及运算与求解能力，属于基础题.

















所挂物体质量x/kg
0
1
2
3
4
5
弹簧长度y/cm
18
20
22
24
26
28
燃烧时间x（min）
10
20
30
40
50
…
剩余长度y（cm）
19
18
17
16
15
…
行驶路程x（千米）
100
200
300
400
油箱内剩油量y（升）

40

24
所挂物体质量x/kg
0
1
2
3
4
5
弹簧长度y/cm
18
20
22
24
26
28
温度
…
﹣20
﹣10
0
10
20
30
…
声速
…
318
324
330
336
342
348
…
距离地面高度（千米）
0
1
2
3
4
5
温度（℃）
20
14
8
2
﹣4
﹣10
销售单价(元)
6
7
8
9
10
11
12
日销售量(桶)
480
440
400
360
320
280
240