高中数学北师大版 (2019)必修 第一册3.1 指数函数的概念导学案

这是一份高中数学北师大版 (2019)必修 第一册3.1 指数函数的概念导学案，共18页。学案主要包含了教学目标，知识清单，基础过关，经典例题，课堂达标，能力提升，参考答案等内容，欢迎下载使用。

【教学目标】


重点、难点


1、理解函数的概念；（重点）


2、会求函数的定义域；（重点）


3、在集合对应的基础上理解函数的概念，并能应用函数的有关概念解题。（难点）


学科素养


通过学习本节内容培养学生的数学抽象核心素养；


通过求函数的定义域、值域等问题，提升学生的数学运算核心素养。


【知识清单】


函数的有关概念


一般地，给定两个 实数集A与B，以及对应关系f，如果对于集合A中的 实数x，按照对应关系f，在集合B中都有 的实数y＝f(x)与x对应，则称f为定义在集合A上的一个函数，记作： 。


其中x称为自变量，y称为因变量，自变量取值的范围(即数集A)称为这个函数的定义域，所有函数值组成的集合 ，称为函数的值域．


函数的三要素


， ，


3.同一个函数


如果两个函数表达式表示的函数 相同， 也相同(即对自变量的每一个值，两个函数表达式得到的函数值都相等)，则称这两个函数表达式表示的就是同一个函数．


【基础过关】


1．下列三个说法：


①若函数的值域只含有一个元素，则定义域也只含有一个元素；


②若f(x)＝5(x∈R)，则f(π)＝5一定成立；


③函数就是两个集合之间的对应关系．


其中正确说法的个数为( )


A．0 B．1 C．2 D．3


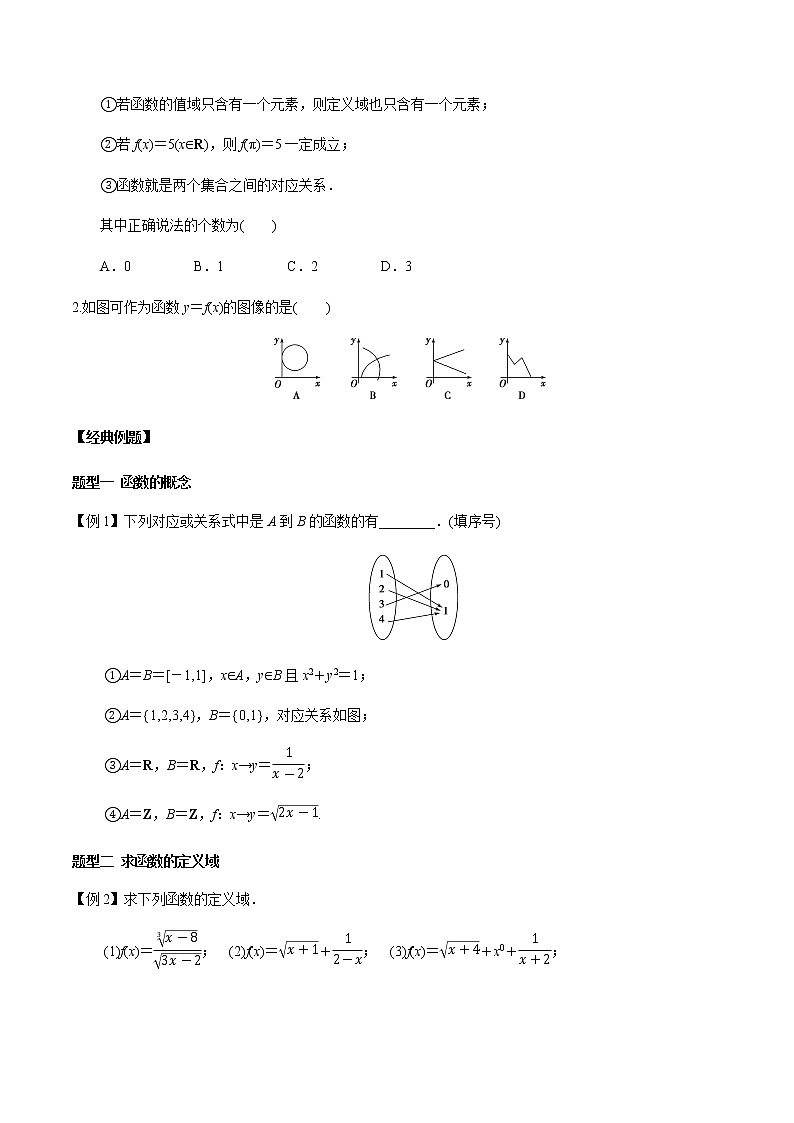
2.如图可作为函数y＝f(x)的图像的是( )





【经典例题】


题型一 函数的概念


【例1】下列对应或关系式中是A到B的函数的有________．(填序号)





①A＝B＝[－1,1]，x∈A，y∈B且x2＋y2＝1；


②A＝{1,2,3,4}，B＝{0,1}，对应关系如图；


③A＝R，B＝R，f：x→y＝eq \f(1,x－2)；


④A＝Z，B＝Z，f：x→y＝eq \r(2x－1).


题型二 求函数的定义域


【例2】求下列函数的定义域．


(1)f(x)＝eq \f(\r(3,x－8),\r(3x－2))； (2)f(x)＝eq \r(x＋1)＋eq \f(1,2－x)； (3)f(x)＝eq \r(x＋4)＋x0＋eq \f(1,x＋2)；














题型三 求函数值


【例3】已知f(x)＝x2－4x＋2，g(x)＝x＋1


(1)求f(2)，f(a)，f(a＋1)的值；（2）求f(g(3))的值











题型三 判断是否为同一个函数


【例4】下列各组函数：


①f(x)＝eq \f(x2－x,x)，g(x)＝x－1；②f(x)＝eq \f(\r(x),x)，g(x)＝eq \f(x,\r(x))；


③f(x)＝eq \r(x＋1)·eq \r(1－x)，g(x)＝eq \r(1－x2)；④f(x)＝eq \r(（x＋3）2)，g(x)＝x＋3.


其中表示同一个函数的是________(填上所有同一个函数的序号)．





【课堂达标】


1．若f(x)＝eq \r(x＋1)，则f(3)＝( )


A．2 B．4


C．2eq \r(2) D．10


2．下列图象表示函数图象的是( )





3.下列四组函数中，表示相等函数的一组是( )


A．f(x)＝|x|，g(x)＝eq \r(x2) B．f(x)＝eq \r(x2)，g(x)＝(eq \r(x))2


C．f(x)＝eq \f(x2－1,x－1)，g(x)＝x＋1 D．f(x)＝eq \r(x＋1)·eq \r(x－1)，g(x)＝eq \r(x2－1).


4.已知，则等于（ ）


A．B．C．D．


5.函数的图象与直线的公共点数目是（ ）


A．1B．0C．0或1D．1或2


6.（多选题）已知，则下列结论正确的是( )


A．B．C． D．


7．已知，则______________.


8．若函数f(x)＝，g(x)＝，则的值为____________.


9.已知函数f(x)＝eq \f(6,x－1)－eq \r(x＋4).


(1)求函数f(x)的定义域；(2)求f(－1)，f(12)的值．




















【能力提升】


1．下列各组函数是同一函数的是（ ）


A．与B．与


C．与 D．与


2．函数的定义域为( )


A．且B．且


C． D．


3．已知函数的定义域为，则的定义域为（ ）


A．B．C．D．


4．已知函数，若，则实数（ ）


A．B．C．2D．9


5．下列函数中，不满足：的是（ ）


A．B．C．D．


6．（多选题）下列说法正确的是（ ）


A．函数值域中的每一个数在定义域中一定只有一个数与之对应


B．函数的定义域和值域可以是空集


C．函数的定义域和值域一定是数集


D．函数的定义域和值域确定后，函数的对应关系也就确定了


E.函数的定义域和对应关系确定后，函数的值域也就确定了


7．（多选题）下列各组函数表示不同函数的是（ ）


A．，B．，


C．，D．，


E.，


8．若函数的定义域为[－2，2]，则函数的定义域为 ______．


9．下列对应或关系式中是A到B的函数的序号为________.


①，；


②A＝{1，2，3，4}，B＝{0，1}，对应关系如图：





③，；


④，.


10．设M＝{x|0≤x≤2}，N＝{y|0≤y≤2}，给出下列四个图形，其中能表示从集合M到集合N的函数关系的是________.





11．已知函数


（1）求函数的定义域；（2）求的值；


（3）求的值（其中且）.











12．已知函数.


（1）求，的值；


（2）求证：是定值；


（3）求的值．

















13．(1)已知函数f(x)的定义域是[1，5]，求函数f(x2＋1)的定义域.


(2)已知函数f(2x2－1)的定义域是[1，5]，求f(x)的定义域.



























































【参考答案】


【知识清单】


1. 非空，每一个，唯一确定，y＝f(x)，x∈A，{y∈B|y＝f(x)，x∈A}


2.定义域，对应关系，值域


3.定义域，对应关系


【基础过关】


1.(2)①错误．若函数的值域只含有一个元素，则定义域不一定只含有一个元素；


②正确．因为f(x)＝5，这个数值不随x的变化而变化，所以f(π)＝5；


③错误．函数就是两个非空数集之间的对应关系．


2.观察图像可知，A，B，C中任取一个x的值，y有可能有多个值与之对应，所以不是函数图像．D中图像是函数图像．


【经典例题】


例1、答案：②


解析：对于①项，x2＋y2＝1可化为y＝±eq \r(1－x2)，显然对任意x∈A，y值可能不唯一，故不符合．对于②项，符合函数的定义．对于③项，2∈A，但在集合B中找不到与之相对应的数，故不符合．对于④项，－1∈A，但在集合B中找不到与之相对应的数，故不符合．


例2、[解析] (1)要使f(x)有意义，则有3x－2>0，∴x>eq \f(2,3)，


即f(x)的定义域为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2,3)，＋∞)).


(2)要使f(x)有意义，则eq \b\lc\{\rc\ (\a\vs4\al\c1(x＋1≥0，,2－x≠0))⇒x≥－1且x≠2，


即f(x)的定义域为[－1,2)∪(2，＋∞)．


(3)要使f(x)有意义，则eq \b\lc\{\rc\ (\a\vs4\al\c1(x＋4≥0，,x≠0，,x＋2≠0，))


解得x≥－4且x≠0，x≠－2，


即f(x)的定义域为[－4，－2)∪(－2,0)∪(0，＋∞)．


例3、[解析] (1)f(2)＝22－4×2＋2＝－2，f(a)＝a2－4a＋2，


f(a＋1)＝(a＋1)2－4(a＋1)＋2＝a2－2a－1.


(2)g(3)＝3＋1＝4，∴f(g(3))＝f(4)＝42－4×4＋2＝2.


例4、【答案】 (1)B (2)③


解析：


①定义域不同，f(x)的定义域为{x|x≠0}，g(x)的定义域为R.


②对应关系不同，f(x)＝eq \f(1,\r(x))，g(x)＝eq \r(x).


③定义域、对应关系都相同．


④对应关系不同，f(x)＝|x＋3|，g(x)＝x＋3.


综上，只有③中两个函数表示同一个函数．


[课堂达标]


1．答案：A.


【解析】


因为f(x)＝eq \r(x＋1)，所以f(3)＝eq \r(3＋1)＝2.


2．答案：C


【解析】


根据函数定义知，对定义域内的任意变量x，都有唯一的函数值y和它对应，即作垂直x轴的直线与图象至多有一个交点(有一个交点即x是定义域内的一个变量，无交点即x不是定义域内的变量)．显然，只有答案C中图象符合．


3.答案：A


【解析】


A中定义域，对应关系都相同，是同一函数；B中定义域不同；C中定义域不同；D中定义域不同．


4.B


【解析】


【分析】


直接代入化简求解即可.


【详解】


解：因为，所以．


故选：B


【点睛】


此题考查由已知函数的解析式求复合函数的解析式，属于基础题.


5.C


【解析】


【分析】


根据函数概念即可判断选择.


【详解】


由函数概念得：对应定义域内每一个自变量有且仅有一个函数值与之对应，


即当在定义域内时，函数的图象与直线的交点有且仅有一个，


当不在定义域内时，函数的图象与直线没有交点，


所以函数的图象与直线的公共点数目是0或1，


故选：C


【点睛】


本题考查函数概念，考查基本分析判断能力，属基础题.


6.BD


【解析】


【分析】


利用换元法求出的解析式，再对选项进行一一验证，即可得答案.


【详解】


令，∴.


∴.


故选：BD.


【点睛】


本题考查换元法求函数的解析式、函数值的求解，考查运算求解能力，属于基础题.


7.8


【解析】


【分析】


先用换元法求出函数解析式，再计算函数值．


【详解】


，则，代入得：


，∴，


∴．


故答案为：8．


【点睛】


本题考查求函数解析式，求函数值，解题方法是换元法．另解：令，则，∴．


8．


【解析】


【分析】


将代入计算，再将代入即可得结果.


【详解】


.


故答案为：


【点睛】


本题考查函数值的求解，属于基础题.


9.【解析】


(1)根据题意知x－1≠0且x＋4≥0，所以x≥－4且x≠1，即函数f(x)的定义域为：


[－4，1)∪(1，＋∞)．


(2)f(－1)＝eq \f(6,－2)－eq \r(－1＋4)＝－3－eq \r(3).


f(12)＝eq \f(6,12－1)－eq \r(12＋4)＝eq \f(6,11)－4＝－eq \f(38,11).


【能力提升】


1．B


【解析】


试题分析：取，由图象可知，此时注水量大于容器容积的，故选B.


考点：函数图像．


2．A


【解析】


【分析】


由公路上行驶的汽车，每个行驶的时间，都有唯一的速度对应，结合函数的概念，即可求解.


【详解】


由题意，公路上行驶的汽车，每个行驶的时间，都有唯一的速度，


所以两个变量“时间”与“速度”之间是函数关系.


故选：A.


【点睛】


本题主要考查了函数概念及其应用，其中解答中熟记函数的基本概念，合理判定是解答的关键，着重考查分析问题和解答问题的能力，属于基础题.


3．（1）距离地面的高度，温度；（2）t＝﹣6h+20；（3）﹣22℃


【解析】


【分析】


（1）由于温度是随高度的变化而变化的，所以自变量是距离地面的高度，因变量是温度，


（2）由表中的数据可知，高度每增加1千米，温度降低6℃，所以两个变量之间是一次函数的关系，所以利用待定系数法求解函数关系式；


（3）直接用（2）中得到的关系式求解


【详解】


（1）由图可知，


表中自变量是距离地面的高度，因变量是温度，


（2）设t＝kh+b，


则， 得，


即h与t关系是：t＝﹣6h+20；


（3）当h＝7时，t＝﹣6×7+20＝﹣22（℃）．


所以距离地面7千米的高空温度是﹣22℃


【点睛】


此题考查了两变量间的关系，属于基础题.


4．（1）随着单价的提高，日销售量在减少，销售单价每提高1元，日销售量减少40桶，销售单价与日销售量之间为函数关系；（2）单价确定为11.5元，获得最大利润为1490元.


【解析】


【分析】


（1）由销售单价与日销售量的表格可知，销售单价与日销量成函数关系；


（2）先求解出日销售量与销售单价的函数关系式，再列出利润关于的解析式，然后确定利润最值及利润最大时销售单价的值.


【详解】


（1）随着单价的提高，日销售量在减少，销售单价每提高1元，日销售量减少40桶，销售单价与日销售量之间为函数关系；


（2）设销售单价为元，获得的利润为元.设日销售量满足：，


由图表可知，日销售量为：，解得，，


即，


根据题意得，


即


当时，


所以单价确定为11.5元，获得最大利润为1490元.


【点睛】


本题考查二次函数的实际应用问题，考查学生处理问题分析问题的能力，难度一般.解答时，关键在于列出利润关于销售单价的函数关系式，然后利用二次函数的性质求解最值.


5．（1）共行驶了22分钟，期间的最大速度为80千米/小时，有4个时间点车速为20千米/小时；（2）函数关系式，发12分钟时车速为20千米/小时.


【解析】


【分析】


（1）根据某辆汽车的行驶情况记录的函数图象，可得该汽车共行驶时间，以及最大速度和车速为20千米/小时的时间点，得到答案；


（2）在出发10分钟到18分钟这段时间中，设为，根据表中的数据列出方程组，即可求得速度与时间的函数关系式，进而得到答案.


【详解】


（1）根据某辆汽车的行驶情况记录的函数图象，可得该汽车共行驶了分钟，


期间的最大速度为80千米/小时，有4个时间点车速为20千米/小时；


（2）在出发10分钟到18分钟这段时间中，速度与时间是一次函数关系，


设为，


由图表中的数据，可得当时，，当时，，


代入得，解得，


所以速度(千米/小时)与时间(分钟)的函数关系式：，其中


当时，即，解得，即出发12分钟时车速为20千米/小时.


【点睛】


本题主要考查了一次函数的解析式的求解，以及函数的图象的识别与应用，着重考查数形结合思想，以及运算与求解能力，属于基础题.