北师大版八年级上册2 平方根教学设计及反思

这是一份北师大版八年级上册2 平方根教学设计及反思，共13页。教案主要包含了知识导图，总结与反思等内容，欢迎下载使用。

第4讲


讲




















平方根














通过对本节课的学习，你能够：


掌握平方根与算数平方根的概念及性质.


灵活应用平方根与算数平方根.























概 述














概 述














【知识导图】














教学过程








一、导入








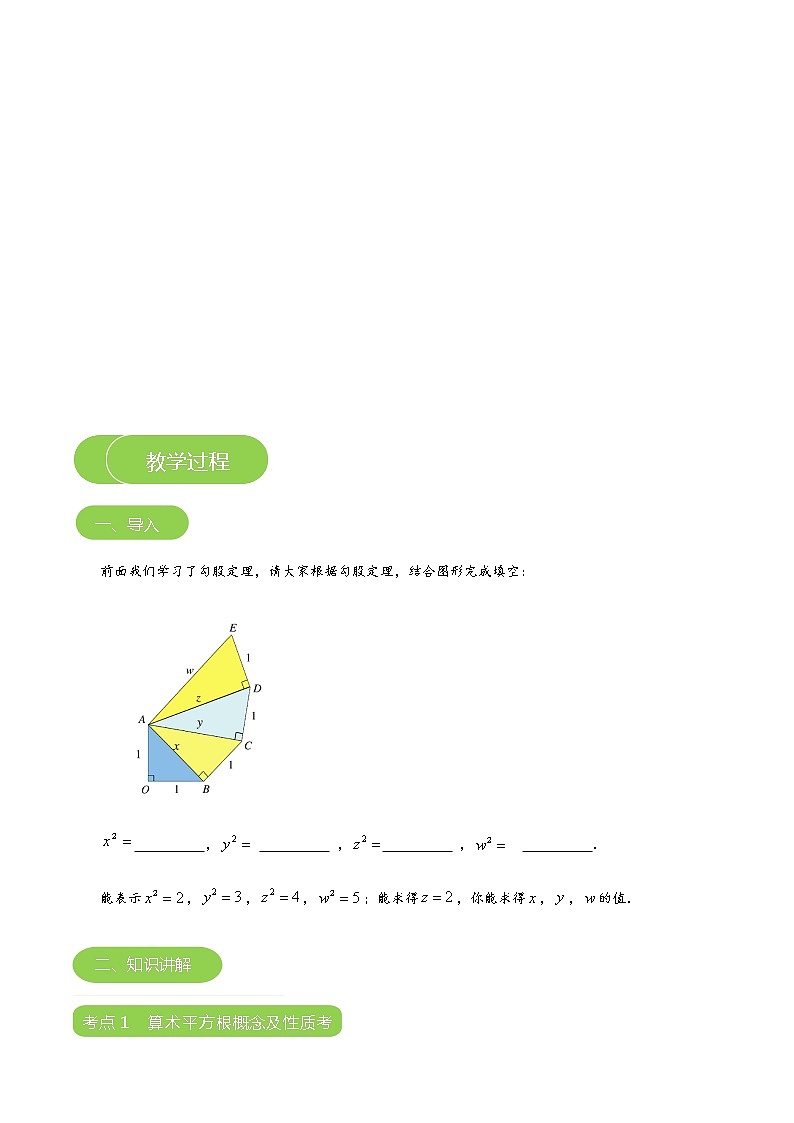
前面我们学习了勾股定理，请大家根据勾股定理，结合图形完成填空：





， ， ， ．


能表示，，，；能求得，你能求得，，的值．





二、知识讲解








考点1 算术平方根概念及性质考点1 生活中的立体图形








，，，，已知幂和指数，怎么求求底数呢？


我们知道：112=121 122=144 132=169 142=196 152=225 那么


在上面思考的基础上，明晰概念：


一般地，如果一个正数的平方等于，即，那么这个正数就叫做的算术平方根，记为“”，读作“根号”．特别地，我们规定0的算术平方根是0，即．


由平方根的定义可知，当，，，那么，，．


由算术平方根的定义我们可知：的算术平方根是一个非负数；我们知道0²=0，正数x=a＞0，所以≥0.


即算术平方根定义中：中的是一个非负数，的算术平方根也是一个非负数，负数没有算术平方根．这也是算术平方根的性质——双重非负性．





考点2 平方根概念及性质








平方根的概念


我们知道1²=（-1）²=1, 2²=（-2）²=4, 3²=（-3）²=9,……,a²=（-a）²=a²,


如果一个数x的平方等于a,即x²=a 。那么x就叫做a的平方根。


正数a的两个平方根可以用“”表示，其中表示a的正的平方根（又叫算术平方根），读作“根号a”； －表示a的负的平方根，读作“负根号a”。


①一个正数a的平方根有两个，记为 ，它们互为相反数。


②0的平方根是0。


③负数没有算数平方根。





考点3 开平方





求一个数a的平方根的运算叫做开平方，a叫做被开方数。（开平方与平方互为逆运算）





三 、例题精析三 、例题精析











类型一 算术平方根概念及性质


例1 求下列各数的算术平方根：


(1) 900； (2) 1； (3) ； (4) 14．


【解析】














【总结与反思】





例2 自由下落物体的高度(米)与下落时间(秒)的关系为．有一铁球从19.6米高的建筑物上自由下落，到达地面需要多长时间？








【解析】














【总结与反思】





例3 则xy=


【解析】














【总结与反思】


类型二 平方根及性质


1.如果x²=a，那么下列说法错误是（ ）


A．若x确定，则a的值是唯一的 B．若a确定，则x的值是唯一的


C．a是x的平方 D．x是a的平方根


【解析】














【总结与反思】





2. 的意义是（ ）


A．a的平方根 B．a的算术平方根 C．当a≥0时，是a的平方根 D．以上都不正确


【解析】














【总结与反思】








例题1


2.若+（y+2）²=0，则等于（ ）


A．﹣1 B．1 C． D．


【解析】











【总结与反思】





类型三：利用平方根的意义求字母的值





【例题】


1.一个正数的平方根是2a﹣3与a﹣12，则这个正数为（ ）


A．3 B．5 C．7 D．49


【解析】














【总结与反思】








四 、课堂运用








基础








1. 的平方根是（ ）


A．±4 B．4 C．±2 D．2











2．下列运算正确的是（ ）


A．﹣ =13 B． =﹣6 C．﹣ =﹣5 D． =±3




















巩固








1.若正方形的边长为a，面积为s，则（ ）


A．s的平方根是a B．a是s的算术平方根 C．a=±s D.s=a


2.4的平方根是 ；3的平方根是 的平方根是 , 的平方根是________．











3.若（a－1）²＋|b－9|＝0，则的平方根是 ．














拔高








1.已知实数a满足条件|2011﹣a|+=a，那么a﹣2011²的值为（ ）


A．2010 B．2011 C．2012 D．2013











2．用代数式表示实数a（a＞0）的平方根：














3．观察下列各式：，，，…请你找出其中规律，并将第n（n≥1）个等式写出来




















五 、课堂小结


























六 、课后作业








1.求下列各式的值：


（1）； （2）； （3）．














2.计算：


（1）﹣； （2）； （3）； （4）±．




















巩固








1.已知一个正数的平方根是m+3和2m-15．


（1）求这个正数-是多少？


（2）的平方根又是多少？








2.如果有意义，那么代数式|x－1|+的值为（ ）


A.±8B.8 C.与x的值无关D.无法确定











3.如果=2,那么(x+3)²=______.

















拔高








若，求的值.











若，求xy的值.











设a、b是有理数，且满足，求的值














适用学科
初中数学
适用年级
初二
适用区域
北师版区域
课时时长（分钟）
120
知识点
1.算数平方根的概念


2.平方根的概念


3. 平方根与算数平方根的应用
教学目标
1.了解平方根与算数平方根的概念。


2.掌握平方根与算数平方根的区别与联系。


3.灵活应用平方根与算数平方根。
教学重点
平方根与算术平方根的概念、性质
教学难点
算数平方根的意义
1．已知边长求面积
正方形边长
正方形面积
2.已知面积求边长
正方形边长
正方形面积
11
121
13
169
0.3
0.09
1
2