初中数学北师大版九年级上册6 应用一元二次方程教学设计及反思

这是一份初中数学北师大版九年级上册6 应用一元二次方程教学设计及反思，共19页。教案主要包含了教学建议，知识导图，总结与反思等内容，欢迎下载使用。

第7讲


讲























应用一元二次方程












































概 述














【教学建议】


一元二次方程的应用是中考中的热门考点，因此学习本讲时要要求学生务必将各个题型都完整的计算一遍，以求做到心中有数，在做题中能够得心应手.


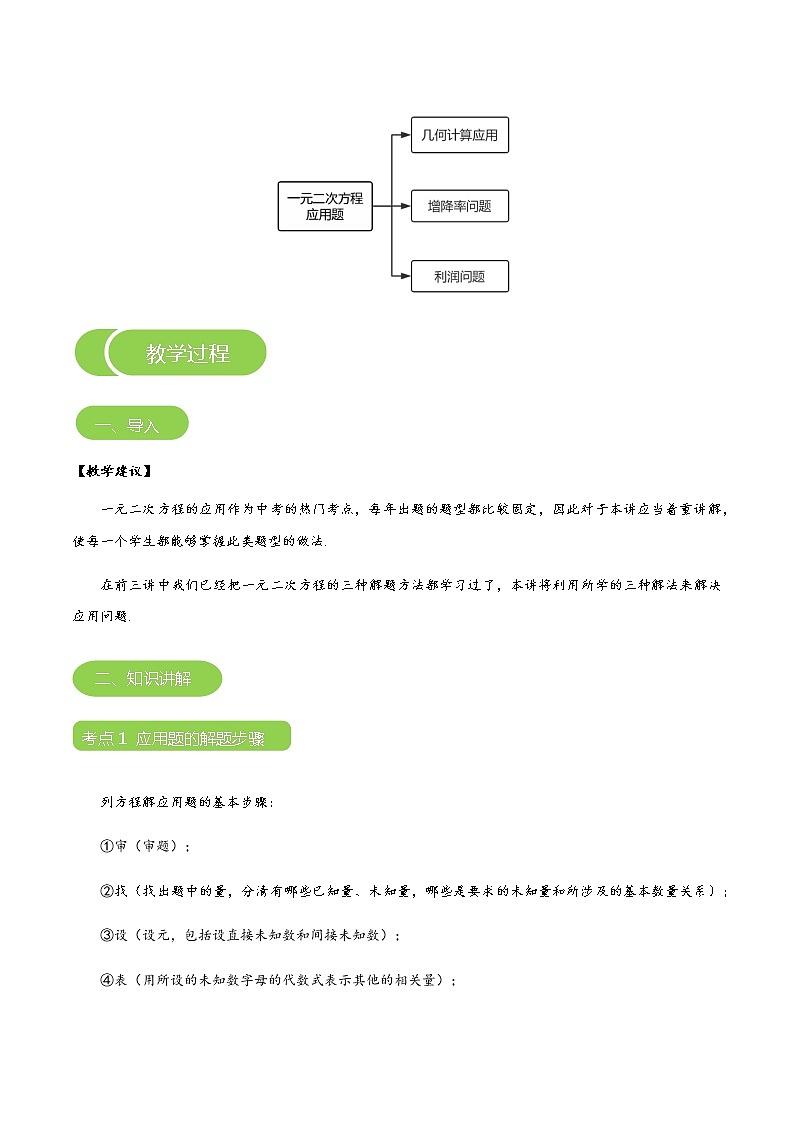
【知识导图】











教学过程








一、导入








【教学建议】


一元二次方程的应用作为中考的热门考点，每年出题的题型都比较固定，因此对于本讲应当着重讲解，使每一个学生都能够掌握此类题型的做法.


在前三讲中我们已经把一元二次方程的三种解题方法都学习过了，本讲将利用所学的三种解法来解决应用问题.





二、知识讲解








考点1 应用题的解题步骤








列方程解应用题的基本步骤：


①审（审题）；


②找（找出题中的量，分清有哪些已知量、未知量，哪些是要求的未知量和所涉及的基本数量关系）；


③设（设元，包括设直接未知数和间接未知数）；


④表（用所设的未知数字母的代数式表示其他的相关量）；


⑤列（列方程）；


⑥解（解方程）；


⑦检验（注意根的准确性及是否符合实际意义）.





三 、例题精析








类型一 几何计算应用





例题1








已知：如图3-9-3所示，在△中，.点从点开始沿边向点以1cm/s的速度移动，点从点开始沿边向点以2cm/s的速度移动.


如果分别从同时出发，那么几秒后，△的面积等于4cm2？


如果分别从同时出发，那么几秒后，的长度等于5cm？


在（1）中，△的面积能否等于?说明理由.





【解析】设t秒后,则：AP=tcm,BP=(5−t)cm；BQ=2tcm.


(1)S△BPQ=BP×BQ×,即4=(5−t)，


解得：t=1或4.(t=4秒不合题意,舍去)


故：1秒后,△PBQ的面积等于4cm2.


(2)PQ=5,则PQ2=25=BP2+BQ2,即25=(5−t)2+(2t)2,t=0(舍)或2.


故2秒后，PQ的长度为5cm.


(3)令S△BPQ=7,即：BP×BQ×=7,(5−t) =7，


整理得：t2−5t+7=0.


由于b2−4ac=25−28=−3<0，则方程没有实数根。


所以,在(1)中,△PQB的面积不等于7cm2.


【总结与反思】本题考查了在几何题中应用一元二次方程求解的题型，比较有代表性.





类型二 增降率问题





例题1








在国家政策的宏观调控下，某市的商品房成交均价由2011年10月底的20000元/m2下降到2011年12月底的16200元/m2.


（1）求2011年11、12两月平均每月降价的百分率是多少？


（2）如果房价继续按此降价的百分率回落，请你预测到2012年2月底该市的商品房成交均价是否会跌破13000元/m2？并说明理由


【解析】(1)设1、12两月平均每月降价的百分率是x，


则11月份的成交价是20000−20000x=20000(1−x)，


12月份的成交价是


20000(1−x)−20000(1−x)x


=20000(1−x)(1−x)


=20000(1−x)2


则20000(1−x)2=16200，


(1−x)2=0.81，


解得x1=10%，x2=1.9(不合题意,舍去).


答：11、12两月平均每月降价的百分率是10%；


(2)如果按此降价的百分率继续回落，


则估计2012年2月份该市的商品房成交均价为


16200(1−x)2


=16200×0.81


=13122>13000，


由此可知2012年2月份该市的商品房成交均价不会跌破13000元/m2.


【总结与反思】 此题考察在増降率题型中一元二次方程的应用，此类题型做题方法比较固定.





类型三 利润问题





例题1








超市以每件50元的价格购进800件T恤，第一个月以单价80元销售，售出了200件；第二个月如果单价不变，预计仍可售出200件.超市为增加销售量，决定降价销售，根据市场调查，单价第降低1元，可多售出10件，但最低单价应高于购进的价格；第二个月结束后，超市将对剩余的T恤一次性清仓销售，清仓时单价为40元，设第二个月单价降低x元.


（1）完成下表（不化简）


（2）如果超市希望通过销售这批T恤获利9000元，那么第二个月的单价是多少元？


【解析】（1）80-x，200+10x，800-200-（200+10x）





（2）根据题意，得


80×200+（80-x）（200+10x）+40[800-200-（200+10x）]-50×800=9000


整理得10x2-200x+1000=0，


即x2-20x+100=0，


解得x1=x2=10


当x=10时，80-x=70＞50


答：第二个月的单价应是70元．


【总结与反思】此题考察了一元二次方程在利润问题中的应用，是中考中比较重要的一类题型.








四 、课堂运用








基础








1.某机械厂七月份生产零件50万个，第三季度生产零件196万个．设该厂八、九月份平均每月的增长率为x，那么x满足的方程是( )


A．50(1＋x2)＝196


B．50＋50(1＋x2)＝196


C．50＋50(1＋x)＋50(1＋x)2＝196


D．50＋50(1＋x)＋50(1＋2x)＝196


2.如图，某农场要建一个长方形的养鸡场，鸡场的一边靠墙，墙长25m，另外三边用木栏围着，木栏长40m．





（1）若养鸡场面积为200m2，求鸡场靠墙的一边长．


（2）养鸡场面积能达到250m2吗？如果能，请给出设计方案，如果不能，请说明理由．








答案与解析


1.【答案】C


【解析】根据题意可得.


2.【答案】见解析


【解析】（1）设宽为米，长（）米，根据题意得：，


，


解得：，


则鸡场靠墙的一边长为：=20（米），


答：鸡场靠墙的一边长20米．


（2）根据题意得：，∴，


∵，∴方程无实数根，


∴不能使鸡场的面积能达到250m2．








巩固








1.如图所示，我海军基地位于A处，在其正南方向200海里处有一重要目标B，在B的正东方向200海里处有一重要目标C，小岛D恰好位于AC的中点，岛上有一补给码头；小岛F位于BC上且恰好处于小岛D的正南方向，一艘军舰从A出发，经B到C匀速巡航．一艘补给船同时从D出发，沿南偏西方向匀速直线航行，欲将一批物品送往军舰.


（1）小岛D和小岛F相距多少海里？


（2）已知军舰的速度是补给船的2倍，军舰在由B到C的途中与补给船相遇于E处，那么相遇时补给船航行了多少海里？（精确到0.1海里）





2.电动自动车已成为市民日常出行的首选工具．据某市某品牌电动自行车经销商1至3月份统计，该品牌电动自行车1月份销售150辆，3月份销售216辆．


（1）求该品牌电动自行车销售量的月均增长率；


（2）若该品牌电动自行车的进价为2300元，售价为2800元，则该经销商1至3月共盈利多少元？





答案与解析


1.【答案】（1）100海里；（2）118.4海里.


【解析】（1）F位于D的正南方向，则DF⊥BC.因为AB⊥BC，D为AC的中点，所以DF＝AB＝100海里，所以，小岛D与小岛F相距100海里.


（2）设相遇时补给船航行了x海里，那么DE＝x海里，AB+BE＝2x海里，EF＝AB+BC－(AB+BE)－CF＝(300－2x)海里.


在Rt△DEF中，根据勾股定理可得方程x2＝1002+(300－2x)2，整理，得3x2－1200x+100000＝0.解这个方程，得x1＝200－≈118.4，x2＝200+（不合题意，舍去）.


所以，相遇时补给船大约航行了118.4海里.


2.【答案】(1) 20%．(2) 273000元.


【解析】（1）设该品牌电动自行车销售量的月均增长率为x，根据题意列方程：


150（1+x）2=216，


解得x1=-220%（不合题意，舍去），x2=20%．


答：求该品牌电动自行车销售量的月均增长率20%．


（2）二月份的销量是：150×（1+20%）=180（辆）．


所以该经销商1至3月共盈利：（2800-2300）×（150+180+216）=500×546=273000（元）．








拔高








1.今年我国多个省市遭受严重干旱，受旱灾的影响，4月份，我市某蔬菜价格呈上升趋势，其前四周每周的平均销售价格变化如表：


（1）请观察题中的表格，用所学过的一次函数、反比例函数或二次函数的有关知识直接写出4月份y与x 的函数关系式；


（2）进入5月，由于本地蔬菜的上市，此种蔬菜的平均销售价格y（元/千克）从5月第1周的2.8元/千克下降至第2周的2.4元/千克，且y与周数x的变化情况满足二次函数y=﹣x2+bx+c，请求出5月份y与x的函数关系式；


（3）若4月份此种蔬菜的进价m（元/千克）与周数x所满足的函数关系为m=x+1.2，5月份此种蔬菜的进价m（元/千克）与周数x所满足的函数关系为m=x+2．试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大？且最大利润分别是多少？





答案与解析


1.【答案】见解析


【解析】（1）通过观察可见四月份周数y与x 的符合一次函数关系式，设这个关系式为：


则，


解得：，


∴4月份y与的函数关系式为；


（2）将（1，2.8）（2，2.4）代入


可得：


解之：


即


（3）4月份此种蔬菜利润可表示为：W1=y﹣m=（0.2+1.8）﹣（+1.2），即：W1=﹣0.05+0.6；


由函数解析式可知，四月份的利润随周数的增大而减小，所以应在第一周的利润最大，最大为：W=﹣0.05×1+0.6=0.55（元/千克），


5月份此种蔬菜利润可表示为：


即：


由函数解析式可知，五月份的利润随周数变化符合二次函数且对称轴为：x=﹣=﹣，


即在第1至4周的利润随周数的增大而减小，所以应在第一周的利润最大，最大为：W=﹣+1.1=1（元/千克）．








五 、课堂小结








一元二次方程解应用题的题型中以利润问题应用最为广泛，其考试热度也是最高的，此部分题目难度较为适中，是易于掌握的一部分题型.








六 、课后作业











基础








1.如图，△ABC中，∠C=90°，AC=8cm，BC=4cm，一动点P从C出发沿着CB方向以1cm/S的速度运动，另一动点Q从A出发沿着AC方向以2cm/S的速度运动，P，Q两点同时出发，运动时间为t（s）．





（1）当t为几秒时，△PCQ的面积是△ABC面积的 ？


（2）△PCQ的面积能否为△ABC面积的一半？若能，求出t的值；若不能，说明理由．


2.近年来，某县为发展教育事业，加大了对教育经费的投入，2009年投入6000万元，2011年投入8640万元．


（1）求2009年至2011年该县投入教育经费的年平均增长率；


（2）该县预计2012年投入教育经费不低于9500万元，若继续保持前两年的平均增长率，该目标能否实现？请通过计算说明理由．


.3.某商店准备进一批季节性小家电，单价40元。经市场预测，若销售定价为52元时，可售出180个；定价每增加1元，销售量将减少10个，定价每减少1元，销售量将增加10个。


(1)商店若准备获利2000元，则定价为多少元?应进货多少个?


(2)请你为商店估算一下，当定价为多少元时，获得的利润最大?并求最大利润。


答案与解析


1.【答案】见解析


【解析】（1）∵S△PCQ=t（8﹣2t），S△ABC=×4×8=16，


∴t（8﹣2t）=16×，


整理得t2﹣4t+4=0，


解得t=2．


答：当t=2s时△PCQ的面积为△ABC面积的；


（2）当S△PCQ=S△ABC时，t（8﹣2t）=16×，


整理得t2﹣4t+8=0，


△=（﹣4）2﹣4×1×8=﹣16＜0，


∴此方程没有实数根，


∴△PCQ的面积不可能是△ABC面积的一半．


2.【答案】见解析


【解析】（1）设每年平均增长的百分率为x．


6000（1+x） 2=8640，


（1+x） 2=1.44，


∵1+x＞0，


∴1+x=1.2，


x=20%．


答：每年平均增长的百分率为20%；


（2）2012年该县教育经费为8640×（1+20%）=10368（万元）＞9500万元．


故能实现目标．


3.【答案】见解析


【解析】（1）设定价为x元,则进货为180−10(x−52)=180−10x+520=(700−10x)个，


所以(x−40)(700−10x)=2000，


解得x1=50,x2=60；


当x=50时，700−10x=700−10×50=200个；


当x=60时，700−10x=700−10×60=100个；


答：商店若准备获利2000元，则定价为50元，应进货200个；或定价为60元，应进货100个；


（2）设利润为w,则


w=(x−40)(700−10x)


=−10x2+1100x−28000


=−10(x−55)2+2250，


因此当x=55时,w最大=2250元；


答：当定价为55元时，获得的利润最大，最大利润是2250元。





巩固








1.某汽车销售公司6月份销售某厂家的汽车，在一定范围内，每部汽车的进价与销售有如下关系，若当月仅售出1部汽车，则该部汽车的进价为27万元，每多售一部，所有出售的汽车的进价均降低0.1万元/部。月底厂家根据销售量一次性返利给销售公司，销售量在10部以内，含10部，每部返利0.5万元，销售量在10部以上，每部返利1万元。


① 若该公司当月卖出3部汽车，则每部汽车的进价为 万元；


② 如果汽车的销售价位28万元/部，该公司计划当月盈利12万元，那么要卖出多少部汽车？（盈利=销售利润+返利）


2.某商店经销甲、乙两种商品． 现有如下信息：





请根据以上信息，解答下列问题：


（1）甲、乙两种商品的零售单价分别为______元和______元．（直接写出答案）


（2）该商店平均每天卖出甲商品500件和乙商品1200件．经调查发现，甲种商品零售单价每降0.1元，甲种商品每天可多销售100件．为了使每天获取更大的利润，商店决定把甲种商品的零售单价下降m（m＞0）元．在不考虑其他因素的条件下，当m定为多少时，才能使商店每天销售甲、乙两种商品获取的利润共1700元？





答案与解析


1.【答案】见解析


【解析】（1）由题意，得


每部汽车的进价为:27−0.1(4−1)=26.7万元，


汽车销售公司月盈利为:4(28−26.7)+4×0.5=7.2万元；


故答案为:26.7，7.2；


（2）设该公司需售出x部汽车。由题意知:


每部汽车的销售利润为28−[27−0.1(x−1)]=(0.1x+0.9)万元。


当0⩽x⩽10时，由题意得:x(0.1x+0.9)+0.5x=12


整理得x2+14x−120=0


解得x1=−20，x2=6


由题知x=−20不合题意舍去，取x=6


当x>10时，由题意得:x(0.1x+0.9)+x=12


整理得x2+19x−120=0


解得x1=−24，x2=5由题知x=−24不合题意舍去，取x=5


因为5<10，所以x=5舍去。


答:该公司需售出6部汽车。


2.【答案】见解析


【解析】解：（1）假设甲、乙两种商品的进货单价各为x，y元，


根据题意得：


解得：


∴甲、乙零售单价分别为2元和3元；


故答案为：2，3；


（2）根据题意得出：





即


解得=0.5或=0（舍去），


答：当定为0.5元才能使商店每天销售甲、乙两种商品获取的利润共1700元．











拔高








1.阅读下列文字


2010年广州亚运会前夕某公司生产一种时令商品每件成本为20元，经市场发现该商品在未来40天内的日销售量为a件，与时间t天的关系如下表：


未来40天内，前20天每天的价格b（元/件）与时间t的关系为b=t+25（1≤t≤20），后20天每天价格为c（元/件）与时间t的关系式为c=﹣t+40（21≤t≤40）解得下列问题


（1）分析表中的数据，用所学过的一次函数，二次函数，反比例函数知识确定一个满足这些数据的a与t的函数关系式；


（2）请预测未来40天中哪一天日销售利润最大，最大日销售利润是多少？


（3）在实际销售的前20天中该公司决定销售一件就捐赠n元（n＜4）利润给亚运会组委会，通过销售记录发现前20天中，每天扣除捐赠后利润随时间t的增大而增大，求n的取值范围．





答案与解析


1.【答案】见解析


【解析】 （1）将代入一次函数a=kt+m，


有


∴a=﹣2t+96，


经检验，其他点的坐标均适合以上解析式


故所求函数的解析式为a=﹣2t+96．


（2）设前20天日销售利润为P1，后20天日销售利润为P2


由P1=（﹣2t+96）（t+5）=﹣t2+14t+480=﹣（t﹣14）2+578，


∵1≤t≤20，∴当t=14时，P1有最大值578元，


由P2=（﹣2t+96）（﹣t+20）=t2﹣88t+1920=（t﹣44）2﹣16，


∵21≤t≤40且对称轴为t=44，∴函数P2在21≤t≤40上随t的增大而减小，


∴当t=21时，P2有最大值为（21﹣44）2﹣16=529﹣16=513（元），


∵578＞513，故第14天时，销售利润最大，为578元．


（3）P3=（﹣2t+96）（t+5﹣n）=﹣t2+（14+2n）t+480﹣96n，


∴对称轴为t=14+2n，


∵1≤t≤20，


∴14+2n≥20得n≥3时，P3随t的增大而增大，


又∵n＜4，


∴3≤n＜4．








七 、教学反思











适用学科
初中数学
适用年级
初三
适用区域
北师版区域
课时时长（分钟）
120
知识点
几何计算的应用


增降率问题


握手问题


利润问题
教学目标
1、掌握列一元二次方程解决实际问题


2、掌握利润问题.
教学重点
能熟练掌握一元二次方程的应用.
教学难点
能熟练掌握一元二次方程的应用.
时间
第一个月
第二个月
清仓时
单价（元）
80
40
销售量（件）
200
周数x
1
2
3
4
价格y（元/千克）
2
2.2
2.4
2.6
时间t（天）
1
3
6
10
36
…
日销售量a（件）
94
90
84
76
24
…