初中北师大版1 成比例线段教案设计

这是一份初中北师大版1 成比例线段教案设计，共17页。教案主要包含了教学建议，知识导图，总结与反思等内容，欢迎下载使用。

第9讲


讲























成比例线段及平行线分线段成比例















































概 述











【教学建议】


相似这一部分知识是整个初中阶段难度较高的一部分，同时也是中考中的热门考点，在教学过程中建议联系全等的知识来学习相似这个知识点.


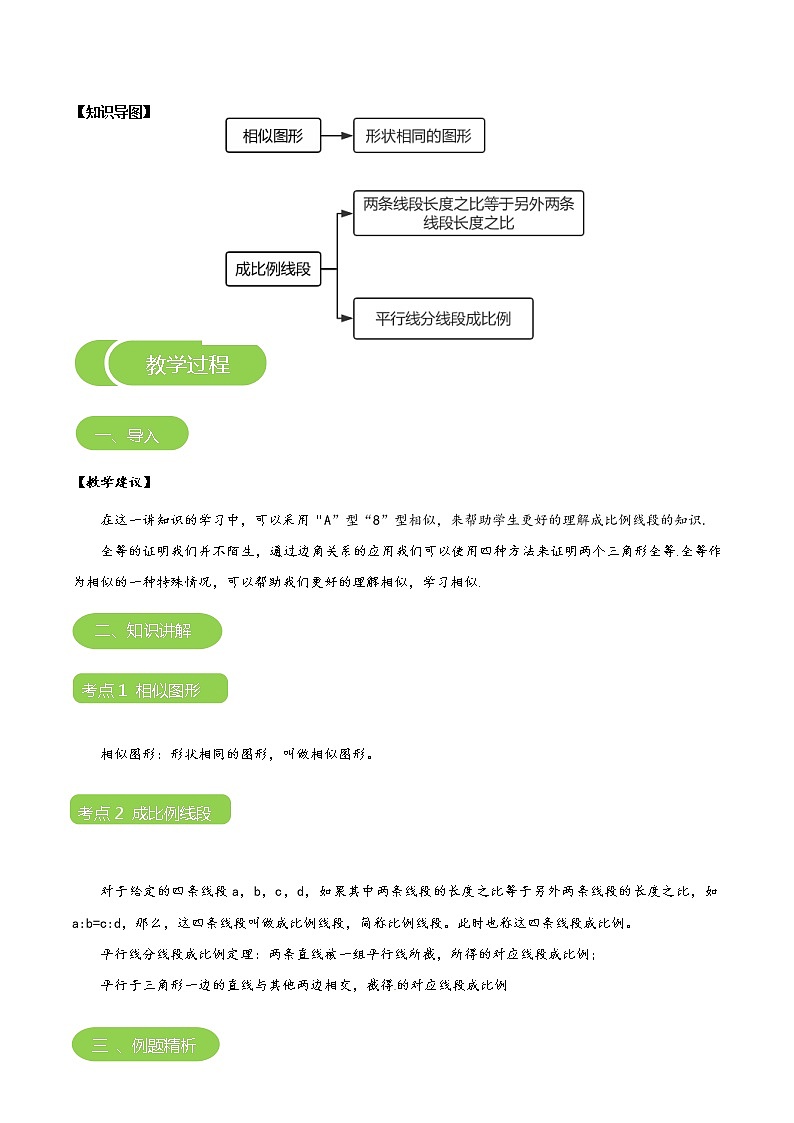
【知识导图】


























教学过程








一、导入








【教学建议】


在这一讲知识的学习中，可以采用“A”型“8”型相似，来帮助学生更好的理解成比例线段的知识.


全等的证明我们并不陌生，通过边角关系的应用我们可以使用四种方法来证明两个三角形全等.全等作为相似的一种特殊情况，可以帮助我们更好的理解相似，学习相似.





二、知识讲解








考点1 相似图形








相似图形：形状相同的图形，叫做相似图形。





考点2 成比例线段











对于给定的四条线段a，b，c，d，如果其中两条线段的长度之比等于另外两条线段的长度之比，如a:b=c:d，那么，这四条线段叫做成比例线段，简称比例线段。此时也称这四条线段成比例。


平行线分线段成比例定理：两条直线被一组平行线所截，所得的对应线段成比例；


平行于三角形一边的直线与其他两边相交，截得的对应线段成比例





三 、例题精析








类型一 成比例线段定义





例题1








下列四组线段中，不构成比例线段的一组是（ ）


A．1 cm，2 cm，3 cm，6 cm


B．2 cm，3 cm，4 cm，6 cm


C．1cm，cm，cm，cm


D．1 cm，2 cm，3 cm，4 cm


【解析】D


D 四个线段的长度不能构成比例式.


【总结与反思】成比例线段对应边成比例.





类型二 比例基本性质的应用





例题1











【解析】见解析


使用代入法，2a=3b，a=b；


=，=，=


【总结与反思】 此题考察了比例性质的应用，是成比例线段中较为常见的类型.





类型三：等比性质的应用





例题1











【解析】①时，k==2；


②=0时，，k=-1


【总结与反思】 此题根据比例的性质，分类讨论即可.





类型四：合比性质的应用





例题1








已知，求+的值。


【解析】根据类型二中的代入法


=3，=，3+=


【总结与反思】此类型考察的是代入法的综合使用.





类型五：平行线分线段成比例的应用





例题1








如图，已知，，，那么的长等于（ ）．





A． B． C． D．


【解析】C


因为 所以BC：BE=3：5，CE：BE=2：5，CE=


【总结与反思】本题考查了几何图形当中成比例线段的计算.








四 、课堂运用








基础








1.下列各组中的四条线段是成比例线段的是（ ）


A．a=6，b=4，c=10，d=5 B．a=3，b=7，c=2，d= 9


C．a=2，b=4，c=3，d=6 D．a=4，b=11，c=3，d=2


2.下列各组线段（单位：㎝）中，成比例线段的是（ ）


A.1、2、3、4 B.1、2、2、4 C.3、5、9、13 D.1、2、2、3


3.比例尺为1:1000000的图纸上某区域面积400cm2，则实际面积为 （ ）


A．4×105 m2 B．4×104 m2 C．1．6×105 m2 D．2×104m2


4.比例5:3=15:9的内项3增加6，要使比例成立，外项9应该增加（ ）


A. 6 B. 18 C. 27 D. 24


5.


6.如图，在△ABC中，点D，E分别在边AB，AC上，DE∥BC．已知AE=6，，则EC的长等于 ．








答案与解析


1.【答案】C


【解析】C 2:4=3:6，其余的选项均不成比例.


2.【答案】B


【解析】B 1:2=2:4，其余的选项均不成比例.


3.【答案】B


【解析】400cm2=0.04m2，0.04×1000000=40000.


4.【答案】B


【解析】 内项积等于外项积，9×15÷5-9=18


5.【答案】3


【解析】 设 =k，x=2k，y=3k，z=4k











6.【答案】8


【解析】8 △ADE和△ABC相似，EC=8.





巩固











1．已知，那么下列等式中，不一定正确的是（ ）


A． B． C． D．


2.知,则下列比例式成立的是 ( )


A． B. C． D．


3.若，且3a-2b+c=3，则2a+4b-3c的值是（ ）


A．14 B．42 C．7 D．


4.如图，已知∠AOB=60°，点P在边OA上，OP=10，点M，N在边OB上，PM=PN，点C为线段OP上任意一点， CD∥ON交PM、PN分别为D、E, 若MN=3，则的值为 ．








5.如图，平行四边形中，是边上的点，交于点，如果，那么 ．








答案与解析


【答案】A


【解析】比例是3:2，具体数值不定.


2.【答案】A


【解析】交叉相乘.


3.【答案】D


【解析】=k，a=5k，b=7k，c=8k


3a-2b+c=15k-14k+8k=3，k=，


2a+4b-3c=10k+28k-24k=14k=.


4.【答案】


【解析】 △PCD和△POM相似，△PDE和PMN相似


，所以.


5.【答案】


【解析】








拔高








1.若，则=__________.


2.已知，则的值为 ．


3.如果（），且，那么=_____





答案与解析


1.【答案】


【解析】，b=2a，d=2c，f=2e，=.


2.【答案】3


【解析】=k，c=4k，b=5k，a=6k，=3


3.【答案】3


【解析】 ，a=bk，c=dk，e=fk，，因此k=3








五 、课堂小结








本节的重要内容：成比例线段及平行线分线段.


成比例线段中最重要的提醒便是代数类计算题，出题方式灵活，计算较为复杂，


平行线分线段涉及到的比例类题型，紧抓住相似A型、8型相似即可.








六 、课后作业











基础








1.若，则= ．


2.已知，则的值为


3.如图，□ABCD中，EF∥AB，DE∶EA = 2∶3，EF = 4，则CD的长（ ）








A．12 B．10 C．8 D．


4.如图，直线，另两条直线分别交，，于点及点，且，，，那么下列等式正确的是（ ）


A


D


E


B


F


C


l1


l2


l3





A． B．


C． D．


5.如图，练习本中的横格线都平行，且相邻两条横格线间的距离都相等，同一条直线上的三个点A、B、C都在横格线上，若线段AB=4 cm，则线段BC= cm





7.如图，在△ABC中，DE∥BC，AD：DB=1：2，DE=2，则BC的长是 ．











答案与解析


1.【答案】


【解析】2a=b.


2.【答案】


【解析】3（a-b）=a，a=


3.【答案】B


【解析】DE∶EA = 2∶3，EF：AB=2:5=4:10


4.【答案】D


【解析】AB：BC=DE：EF，BC×DE=AB×EF=6.


5.【答案】12


【解析】查格数可得.


6.【答案】6


【解析】 AD：DB=1：2，DE：BC=1:3=2:6.

















巩固








1.如果，那么＝（ ）


A． B． C． D．





2.如图，在△ABC中，AD平分∠BAC,按如下步骤作图：第一步，分别以点A、D为圆心，以大于的长为半径在AD的两侧作弧，交于两点M、N;第二步，连结MN，分别交AB、AC于点E、F；第三步，连结DE、DF．．若BD=6，AF=4，CD=3，则BE的长是（ ）





A．2 B．4 C．6 D．8





3.练习：如图，直线l1、l2、…l6是一组等距的平行线，过直线l1上的点A作两条射线，分别与直线l3、l6相交于点B、E、C、F．若BC=2，则EF的长是 ．











4.如图，在△ABC中，AB=AC，DE∥BC，则下列结论中不正确的是（ ）





AD=AE B．DB=EC C．∠ADE=∠C D．DE=BC








5.如图所示，△ABC中，DE∥BC，若，则下列结论中正确的是（ ）





A． B．


C． D．





答案与解析


1.【答案】D


【解析】，3（x+y）=5x，x：y=3:2.


2.【答案】D


【解析】AF=AE=4，BD：CD=6:3=2:1=BE：AE=8:4.


3.【答案】5


【解析】查格数可得


4.【答案】D


【解析】DE不一定是中位线.


5.【答案】B


【解析】DE：BC=1:3.





拔高








1.如图，AD∥BE∥CF，直线l1、l2这与三条平行线分别交于点A、B、C和点D、E、F．已知AB=l，BC=3，DE =2，则EF'的长为（ ）





A．4 B．5 C．6 D．8





2.如图，△ABC中，点D、E分别为AB、AC的中点，连接DE，线段BE、CD相交于点O，若OD=2，则OC=（ ）．





A．3 B．4 C．5 D．6


3.如图，是平行四边形对角线上的点，，则（ ）.





B． C． D．








答案与解析


1.【答案】C


【解析】AB：BC=1:3,DE:EF=2:6


【答案】B


【解析】△CBO与△DEO相似，相似比为2：1，OD：OC=1：2=2:4.


【答案】A


【解析】△BEF∽△DAF，BE：AD=1:3，所以BE：EC=1：2.





七 、教学反思











适用学科
初中数学
适用年级
初三
适用区域
北师版区域
课时时长（分钟）
120
知识点
比例线段定义


比例基本性质的应用


等比性质的应用


合比性质的应用


平行线分线段成比例的应用


平行线分线段成比例推论的应用
教学目标
1、掌握成比例线段的定义及计算.


2、掌握平行线分线段成比例的性质及推论.
教学重点
能熟练掌握平行线的性质与推论.
教学难点
能熟练掌握平行线的性质与推论.