初中数学3.3 整式教案设计

这是一份初中数学3.3 整式教案设计，共15页。教案主要包含了教学建议，知识导图，总结与反思等内容，欢迎下载使用。
第10讲


讲























整式
































.

















概 述














【教学建议】


整式的概念是整式运算的基础。在讲解这一部分的时候，要从实际问题引入，让学生了解概念产生的背景。


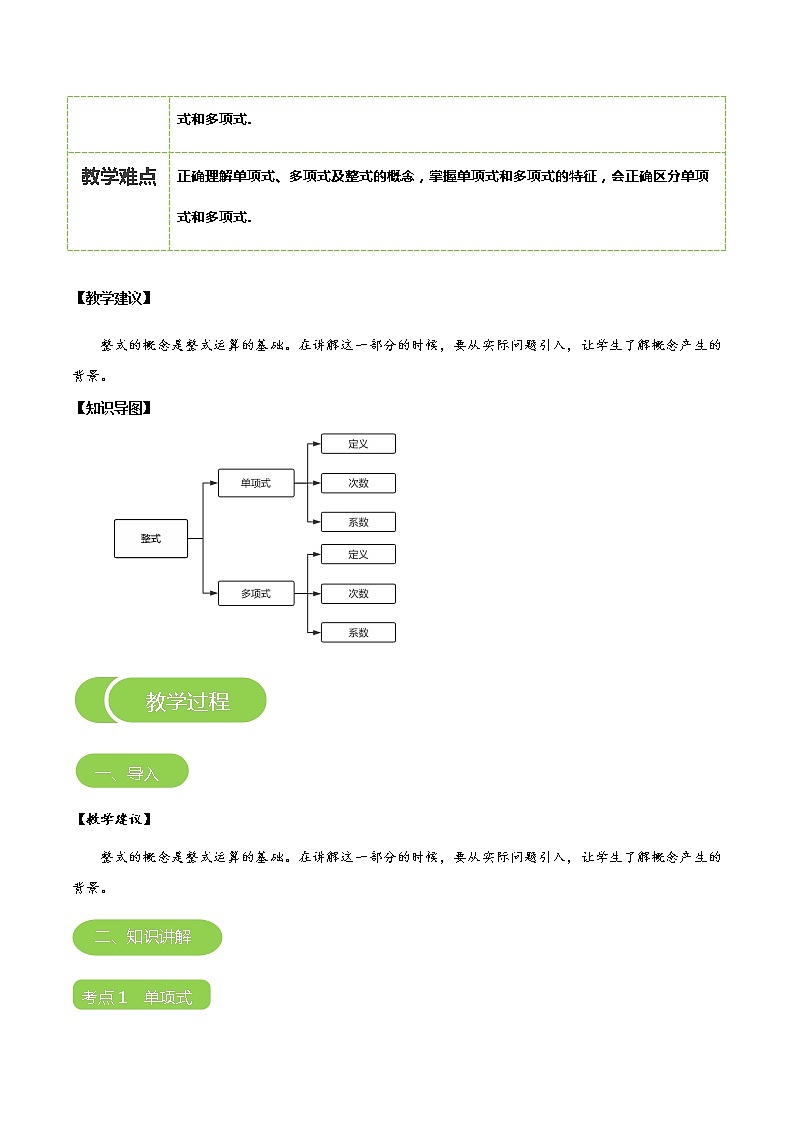
【知识导图】











教学过程








一、导入








【教学建议】


整式的概念是整式运算的基础。在讲解这一部分的时候，要从实际问题引入，让学生了解概念产生的背景。





二、知识讲解








考点1 单项式








单项式：像等，都是数与字母的乘积，这样的代数式叫做单项式.单独一个数或字母也是单项式.


单项式中的数字因数叫做这个单项式的系数，如的系数是，的系数是.所有字母的指数和叫做这个单项式的次数，如都是2次的，是4次的.





考点2 多项式








几个单项式的和叫做多项式,如都是多项式.


在多项式中，每个单项式叫做多项式的项，如多项式是与两项的和.一个多项式中，次数最高的项的次数，叫做这个多项式的次数.如是2次的，是3次的.


整式：单项式和多项式统称为整式.





三 、例题精析








类型一 单项式的定义





例题1








下列式子中单项式的个数是（ ）


3a， ， ， ， -x， ， ， 2015


A.4 B.5 C.6 D.7


【解析】





【总结与反思】





类型二 单项式的系数与次数





例题1








下列说法正确的是（ ）


A.单项式的系数是-2，次数是3


B.单项式b的系数是1，次数是0


C.单项式的系数是2，次数是12


D.单项式的系数是，次数是3


【解析】





【总结与反思】





类型三 单项式与绝对值的综合应用





例题1








如果是关于x，y的六次单项式，求k的值；


【解析】





【总结与反思】








例题1





例题1


类型四 多项式的定义





在下列代数式：中，多项式有（ ）


A.2个 B.3个 C.4个 D.5个


【解析】





【总结与反思】





类型五 多项式的项与次数





例题1








下列说法正确的是（ ）


A.


B.


C.多项式的次数是3


D.一个多项式的次数是6，则这个多项式中只有一项的次数是6


【解析】


【总结与反思】





类型六 多项式与单项式的转化





例题1








当x为何值时，下列多项式可化简为关于y的一次单项式


（1） （2）


【解析】





【总结与反思】





类型七 多项式的实际应用





例题1








用长为12米的木条，做成一个长方形的窗框（如图所示，中间有一横档），


设窗框的横条长度为x米，用代数式表示窗框的面积.


【解析】


【总结与反思】

















四 、课堂运用








基础








1.下列说法错误的是（ ）


A. 不是单项式 B.0不是单项式 C. 是单项式 D. 不是单项式


2.若－mxny是关于x,y的一个单项式，且其系数为3，次数为4，则mn的值为（ ）


A. 9 B.－9 C.12 D.－12


3.在下列式子中，次数为3的单项式（ ）


A. B. C. D.


4.下列说法中，正确的是（ ）


A.单项式一定是含字母的式子 B.单项式a没有系数


C.-y的次数为0 D.单项式-π2x2y的系数是-π2，次数是3


5.在中多项式有（ ）


A.1个 B.2个 C.3个 D.4个


6.下列代数式中，不是整式的是（ ）


A. B. C. D.-2005


7. （1）是五次单项式，则m=__________；


（2）若是五次单项式，则m=__________；











巩固








1.-4a2b的次数是（ ）


A.-4 B.2 C.3 D.4


2.已知三个单项式：①－2x3 ②x2 ③如果按次数从大到小的顺序排列，正确的次序是（ ）


A.①②③ B.③②① C.②③① D.②①③


3.对于多项式的意义解释的不恰当的是（ ）


A.a，b两数的平方和


B.边长分别是a，b的两个正方形的面积和


C.买a支单价为a元的钢笔和b支单价为b元的铅笔总价钱


D.边长是a+b的正方形的面积


4.下列说法错误的是（ ）


A.m是单项式也是整式


B. 是多项式也是整式


C.整式一定是单项式


D.整式不一定是多项式


5.将代数式中是单项式的是_____________________________，是多项式的是_____________________________.


6. 说出下列单项式的系数与次数：


（1）； （2）-mn；


（3）； （4）.


7.已知是x,y的五次单项式，求a的值.


8.是关于x，y的单项式，且系数为8，次数为4，求a，b的值


9.已知单项式与的次数相同。


（1）求m的值；


（2）求当x=-9，y=-2时，单项式的值


























拔高








1.若化简关于x，y的整式得到的结果是一个三次二项式，求的值.


2.观察下列单项式：-x，3x2，-5x3,7x4，···，-37x19,，39x20，···回答下列问题：


（1）这组单项式的系数的符号、绝对值规律是什么？


（2）这组单项式的次数的规律是什么？


（3）根据上面的归纳，你可以猜想出第n个单项式是什么？


（4）请你根据猜想，写出第2014个，第2015个单项式.


3.（1）根据各项系数的符号以及系数的值得出：


这组单项式的系数的符号规律是，系数的绝对值规律是2n-1．


（2）这组单项式的次数的规律是从1开始的连续自然数．


（3）第n个单项式是：．


（4）第2013个单项式是-4025×2013，第2014个单项式是4027×2014．


1.树的高度与树的生长年数有关，测得某种树的有关数据如下表（树苗原高100cm）：


（1）你能用含有字母的代数式表示树苗的高度吗？


（2）生长了16年后的树，高度是多少？


（3）当n=16时，高度是多少？,











五 、课堂小结



































六 、课后作业











基础








1.下列式子中属于单项式的是（ ）


A. B. C. D.


2.对于单项式15a，下列解释不合理的是（ ）


A.家鸡的市场价为15元/kg，买akg家鸡需15a元


B.家鸡的市场价为a元/kg，买15kg家鸡需15a元


C.等边三角形的边长为5a，则这个三角形的周长为15a


D.完成一道工序所需时间是a h，完成15道工序所需的总费用为15a元


3.多项式是（ ）


A.二次二项式 B.三次二项式 C.四次二项式 D.五次二项式


4.下列说法正确的是（ ）


A.整式abc没有系数


B.不是整式


C.-2不是整式


D. 2x+1是整式


5.多项式xy2－8xy+3x2y+25的二次项为（ ）


A.3 B.－8 C.3x2y D.－8xy


6.在代数式中，含y的项的系数是（ ）


A.－3 B.3 C.－ D.


7.在－2，π，2a，x+1，中，整式有（ ）


A.2个 B.3个 C.4个 D.5个


2指出下列各式中哪些是单项式，哪些是多项式，哪些是整式？





单项式：_____________________________


多项式：_____________________________


整式：________________________________








巩固








1.如果n是整数，那么5n（ ）[来源:Z|xx|k.Cm]


A.能被5整除 B.被5除余1 C.被5除余2 D.被5除余3


2.一个n次多项式（n为正整数），它的每一项的次数（ ）


A.都等于n B.都小于n C.都不小于n D.都不大于n


3.单独一个字母一定不是（ ）


A.一次单项式 B.单项式 C.多项式 D.整式


4.下列叙述中，错误的是（ ）


A.－a的系数是－1，次数是1 B.单项式ab2c3的系数是1，次数是5


C.2x－3是一次二项式 D.3x2+xy－8是二次三项式


5.判断下列代数式是否是单项式，如果不是，请简要说明理由；如果是，请指出它的系数与次数：


（1）a； （2） ； （3）；


； （5）xy；


6.已知是关于x，y的五次单项式，求的值。


7.某服装店销售一种品牌服装，其原价为p元，现有两种调价方案：


（1）先提价25%，再降价25%；


（2）先降价25%，再降价25%


按这两种方案调价，结果是否一样？最后是不是都恢复了原价？























拔高








1.若多项式是关于x的二次多项式，则a=_________,b=_________.


2.已知多项式是六次四项式，单项式与该多项式的次数相同，求m，n的值


3.当b为何值时，下列多项式可化简为关于a的一次单项式


（2）


4.从长与宽分别为a与b的长方形中挖去一个圆和一个小半圆，如图所示，用代数式表示剩余部分的面积，并说明该代数式是否为多项式.











七 、教学反思











适用学科
初中数学
适用年级
初一
适用区域
北师版区域
课时时长（分钟）
120
知识点
1、单项式的定义及其次数与系数.


2、单项式与绝对值的综合应用.


3、多项式的定义及其次数与系数.


4、由多项式的概念项数次数求解未知数的值.


5、多项式与单项式的转化.


6、多项式的实际应用.
教学目标
1、经历用字母表示数量关系的过程，在现实情境中进一步理解字母表示数的意义，发展符号感.


2、了解整式产生的背景和整式的概念，能求出整式的次数.


3、进一步发展观察、归纳、分类等能力，发展有条理的思考及语言表达能力.
教学重点
正确理解单项式、多项式及整式的概念，掌握单项式和多项式的特征，会正确区分单项式和多项式.
教学难点
正确理解单项式、多项式及整式的概念，掌握单项式和多项式的特征，会正确区分单项式和多项式.
年数
高度（cm）
1
100＋6
2
100＋12
3
100＋18
4
100＋24
…
…