北师大版七年级上册4.1 线段、射线、直线教学设计

这是一份北师大版七年级上册4.1 线段、射线、直线教学设计，共24页。教案主要包含了教学建议，知识导图，总结与反思等内容，欢迎下载使用。

第12讲


讲























线段、射线、直线及比较线段的长短





























.




















概 述














【教学建议】


本讲是初中几何的基础，在小学阶段已有相关知识的学习，结合小学知识，对各种线有一个更加深入的理解，将会使我们的几何学习事半功倍.


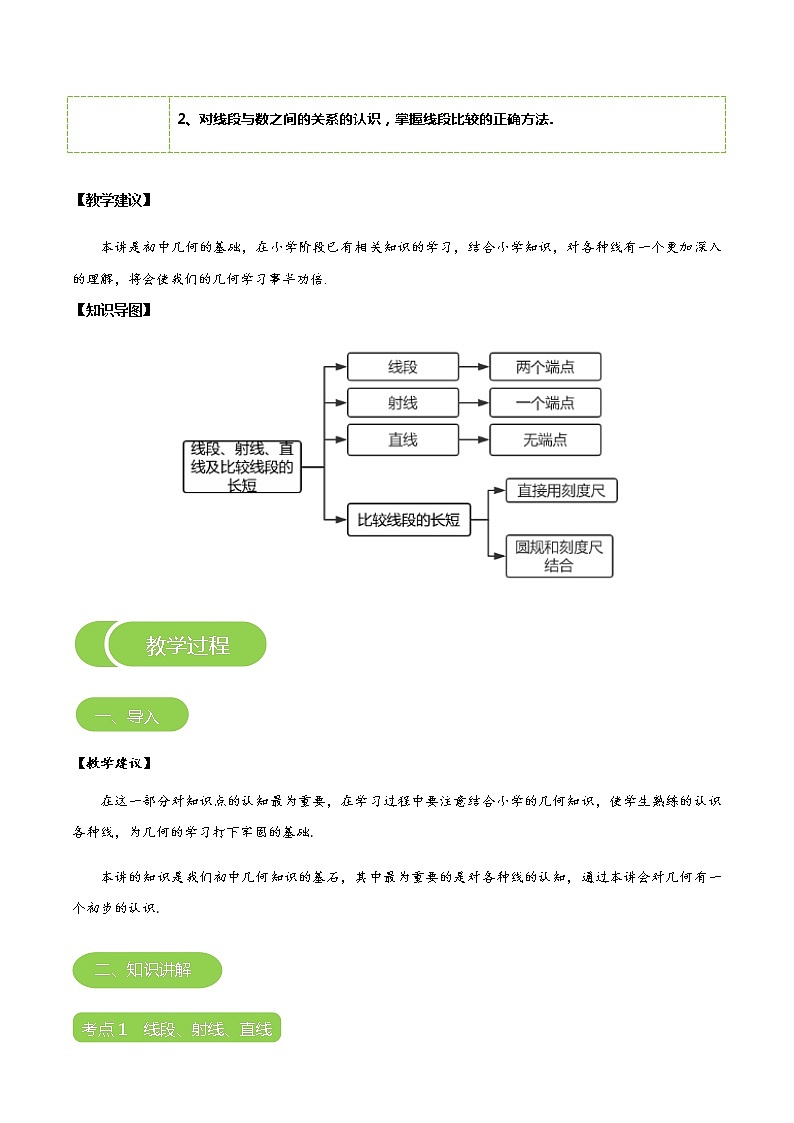
【知识导图】











教学过程








一、导入








【教学建议】


在这一部分对知识点的认知最为重要，在学习过程中要注意结合小学的几何知识，使学生熟练的认识各种线，为几何的学习打下牢固的基础.


本讲的知识是我们初中几何知识的基石，其中最为重要的是对各种线的认知，通过本讲会对几何有一个初步的认识.





二、知识讲解








考点1 线段、射线、直线








1.线段的表示也有两种：一个小写字母或用端点的两个大写字母.但前面必须加“线段”两字，如：线段a；线段AB.


2.射线的表示同样有两种：一个小写字母或端点的大写字母和射线上的要给大写字母，前面必须加“射线”两字


3.直线的表示有两种：一个小写字母或两个大写字母.但前面必须加“直线”两字，如：直线；直线m，直线AB；直线CD





考点2 比较线段的长短








线段的两种度量方法：


(1)直接用刻度尺.


(2)圆规和刻度尺结合使用.





三 、例题精析








类型一 线段、射线、直线的概念





例题1








有下列说法：①电线杆可看做射线，②探照灯光线可看做射线，③A地到B地的高速公路可看做一条直线．其中正确的有（ ）


A.0个 B.1个 C.2个 D.3个


【解析】B


①电线杆是线段


③高速公路也是线段


【总结与反思】根据线段、射线、直线的定义即可判断.





例题2








下列说法中，正确的有（ ）


①过两点有且只有一条直线；


②连结两点的线段叫做两点的距离；


③两点之间，线段最短；


④若AB＝BC，则点B是线段AC的中点；


A．1个 B．2个 C．3个 D．4个


【解析】C


④B不一定在线段AC上


【总结与反思】根据线段、射线、直线的定义即可判断











例题3








下列结论正确的是（ ）


A. 直线比射线长


B. 一条直线就是一个平角


C. 过三点中的任两点一定能作三条直线


D.经过两点有且只有一条直线


【解析】D


A 直线和射线都是无限长


B直线没有端点，不属于角


C 不共线的三个点，可以做三条直线


【总结与反思】根据线段、射线、直线的定义即可判断


类型二 线段、射线、直线的表示方法





例题1








下列四个图中的线段（或直线、射线）能相交的是（ ）





A．（1） B．（2） C．（3） D．（4）


【解析】A


CD是射线，不能与直线AB相交


CD是射线，不能与直线AB相交


CD是线段，不能与直线AB相交





【总结与反思】 根据线段、射线、直线的定义和表示方法即可判断











类型三 两点一线的应用





例题1








把弯曲的河道改直，能够缩短航程，这样做的道理是（ ）





A．垂线段最短


B．两点确定一条直线


C．两点之间，线段最短


D．两点之间，直线最短


【解析】C


两点之间，线段最短


【总结与反思】根据线段、射线、直线的性质判断即可.


.





例题1





例题1


类型四 平面图形的找规律问题








如图，平面内有公共端点的六条射线OA、OB、OC、OD、OE、OF，从射线OA开始按逆时针依次在射线上写出数字1、2、3、4、5、6、7…，则数字“2015”在（ ）





A．射线OA上 B．射线OB上


C．射线OD上 D．射线OE上


【解析】D


6个数是一个循环，，


所以在OE上


【总结与反思】 根据题中的循环节即可解答.





类型五 线段的大小比较





例题1








下列说法中，不正确的是（ ）


（A）若点C在线段BA的延长线上，则BA＝AC－BC


（B）若点C在线段AB上，则AB＝AC+BC


（C）若AC＋BC＞AB，则点C一定在线段BA外


（D）若A、B、C三点不在一直线上，则AB＜AC+BC


【解析】A


BA=CA-CB.


【总结与反思】 根据延长线的定义及性质即可解答.


类型六 线段的中点的定义





例题1








下列说法中正确的是（ ）


A．若AP=AB，则P是AB的中点


B．若AB＝2PB，则P是AB的中点


C．若AP＝PB，则P为AB的中点


D．若AP＝PB=AB，则P是AB的中点


【解析】D


ABC三个选项均不能确定P点是否在线段AB上


【总结与反思】 此类题型根据线段的中点定义即可解答.











类型七 线段的中点的应用





例题1








已知线段AB=16cm,C是线段AB上的一点,且AC=10cm,D为AC的中点,E是BC的中点，求线段DE的长


【解析】8厘米





【总结与反思】 根据中点的定义即可得出..








四 、课堂运用








基础








1.下列说法正确的是（ ）


A.延长射线MN到点P B.延长直线MN到点P


C.延长线段MN到点P D.以上说法都正确


2.手电筒发射出来的光线，给我们的感觉是（ ）


A.线段 B.射线 C.直线 D.折线


3.下列叙述中，正确的是（ ）


A.点A在直线l上 B.直线的一半是射线


C.延长直线AB到C D.射线OA与射线AO是同一条射线


4.经过A、B、C三点的任意两点，可以画出的直线数为（ ）


A.1或2 B.1或3 C.2或3 D.1或2或3


5.延长线段AB到C，下列说法中正确的是（ ）


A．点C在线段AB上


B．点C在直线AB上


C．点C不在直线AB上


D．点C在直线AB的延长线上


6.如图，共有_________条射线．





答案与解析


1.【答案】C


【解析】根据线段、射线、直线的定义即可判断.


2.【答案】A


【解析】根据线段、射线、直线的定义即可判断.


3.【答案】A


【解析】根据线段、射线、直线的定义即可判断.


4.【答案】D


【解析】根据线段、射线、直线的定义即可判断.


5.【答案】D


【解析】根据延长线的定义即可判断.


6.【答案】4


【解析】根据射线的定义即可查出.





巩固








1.如图所示，由A到B有①、②、③三条路线，最短的路线选①的理由是（ ）





A．因为它直 B．两点确定一条直线


C．两点间距离的定义 D．两点之间，线段最短


2.点C是线段AB的中点，点D是线段BC的中点，下列等式不正确的是 （ ）





A．CD=AC－DB B．CD=AD－BC C．CD=AB－AD D．CD=AB－BD


3.开学整理教室时，智慧老师总是先把每一列最前和最后的课桌摆好，然后再依次摆中间的课桌，一会儿一列列整整齐齐的课桌就摆在一条线上了，这是因为 ．


4.已知线段，若为中点，则= ．


5.在数轴上有四个点A、B、C、D，如图，请回答





（1）A、C两点间的距离是多少？


（2）B、D两点之间的距离是多少？


（3）将A点向右移4各单位后，四个点所表示的数谁最小？





答案与解析


1.【答案】D


【解析】两点之间，线段最短.


2.【答案】D


【解析】CD=AB-3BD.


3.【答案】两点确定一条直线


【解析】两点确定一条直线


4.【答案】3


【解析】


5.【答案】（1）;（2）;.


【解析】（1）3-4=7；


（2）


（3）A移动四个单位后为0，最小的是B.





拔高








1.平面内的9条直线任两条都相交，交点数最多有m个，最少有n个，则m+n等于（ ）


A.36 B.37 C.38 D.39


2.从哈尔滨开往某市的特快列车，途中要停靠两个站点，如果任意两站间的票价都不同，那么有多少种不同的票价（ ）


A.3 B.4 C.6 D.12


3.已知线段AB=12cm，在直线AB上有一点C，且BC=4cm，M是线段AC的中点，求线段AM的长.


4.已知数轴上有A，B，C三点，分别表示数－24，－10，10．两只电子蚂蚁甲、乙分别从A，C两点同时相向而行，甲的速度为4个单位/秒，乙的速度为6个单位/秒．


（1）若甲、乙在数轴上的点D相遇，则点D表示的数 ；


（2）问多少秒后甲到A，B，C三点的距离之和为40个单位？若此时甲调头往回走，问甲、乙还能在数轴上相遇吗？若能，求出相遇点；若不能，请说明理由．


（3）若甲、乙两只电子蚂蚁（用P表示甲蚂蚁、Q表示乙蚂蚁）分别从A，C两点同时相向而行，甲的速度变为原来的3倍，乙的速度不变，直接写出它们爬行多少秒后，在原点O、甲蚂蚁P与乙蚂蚁Q三点中，有一点恰好是另两点所连线段的中点.





答案与解析


1.【答案】B


【解析】最少有1个，最多有36个，所以m+n=37个.


原式=.


2.【答案】C


【解析】3+2+1=6.


3.【答案】4或8


【解析】①AC=


②AC=


4.【答案】见解析


【解析】（1）设x秒后甲与乙相遇，则4x+6x=34，


解得 x=3.4，


4×3.4=13.6，-24+13.6=-10.4．


故甲、乙在数轴上的-10.4相遇，故答案为：-10.4；


（2）设y秒后甲到A，B，C三点的距离之和为40个单位，


B点距A，C两点的距离为14+20=34＜40，A点距B、C两点的距离为14+34=48＞40，C点距A、B的距离为34+20=54＞40，故甲应位于AB或BC之间．


AB之间时：4y+（14-4y）+（14-4y+20）=40


解得y=2；


BC之间时：4y+（4y-14）+（34-4y）=40，


解得y=5．


甲从A向右运动2秒时返回，设y秒后与乙相遇．此时甲、乙表示在数轴上为同一点，所表示的数相同．


甲表示的数为：-24+4×2-4y；乙表示的数为：10-6×2-6y，


依据题意得：-24+4×2-4y=10-6×2-6y，


解得：y=7，


相遇点表示的数为：-24+4×2-4y=-44（或：10-6×2-6y=-44），


②甲从A向右运动5秒时返回，设y秒后与乙相遇．


甲表示的数为：-24+4×5-4y；乙表示的数为：10-6×5-6y，


依据题意得：-24+4×5-4y=10-6×5-6y，


解得：y=-8（不合题意舍去），


即甲从A向右运动2秒时返回，能在数轴上与乙相遇，相遇点表示的数为-44．


（3）①设x秒后原点O是甲蚂蚁P与乙蚂蚁Q两点的中点，则


24-12x=10-6x，解得x= ；


设x秒后乙蚂蚁Q是甲蚂蚁P与原点O两点的中点，则


24-12x=2（6x-10），解得x= ；


设x秒后甲蚂蚁P是乙蚂蚁Q与原点O两点的中点，则


2（24-12x）=6x-10，解得x= ；


综上所述，秒或秒或秒后，原点O、甲蚂蚁P与乙蚂蚁Q三点中，有一点恰好是另两点所连线段的中点．








五 、课堂小结











本节讲了2个重要内容：


1.线段、射线、直线的定义及表示方法.


2.比较线段的长短的两种方法：①用刻度尺测量；②用圆规和刻度尺配合比较.











六 、课后作业











基础








1.下列语句正确的是（ ）


A.画直线AB=10厘米 B.画直线l的垂直平分线


C.画射线OB=3厘米 D.延长线段AB到点C，使得BC=AB


2.下列说法错误的是（ ）


A.两点确定一条直线 B.线段是直线的一部分


C.一条直线是一个平角 D.把线段向两边延长即是直线


3.如图所示，关于线段、射线和直线的条数，下列说法正确的是（ ）





A．五条线段，三条射线


B．一条直线，三条线段


C．三条线段，两条射线，一条直线


D．三条线段，三条射线，一条直线


4.同一平面内有四点，每过两点画一条直线，则直线的条数是（ ）


A．1条 B．4条 C．6条 D．1条或4条或6条


5.练习下列说法中，不正确的是（ ）


（A）若点C在线段BA的延长线上，则BA＝AC－BC


（B）若点C在线段AB上，则AB＝AC+BC


（C）若AC＋BC＞AB，则点C一定在线段BA外


（D）若A、B、C三点不在一直线上，则AB＜AC+BC


6.如图，C、B是线段AD上的两点，若AB=CD，BC=2AC，那么AC与CD的关系是为（ ）





CD=2AC B.CD=3AC C.CD=4BD D.不能确定





7.点A、B、C在同一条数轴上，其中点A、B表示的数分别为﹣3、1，若BC=2，则AC等于（ ）


A.3 B.2 C.3或5 D.2或6


8.已知A、B、C三点在同一直线上，那么线段AB、BC、AC三者的关系是（ ）


A．AC=AB+BC B．AC＞AB C．AC＞AB＞BC D．不能确定





答案与解析


1.【答案】D


【解析】根据线段、射线、直线的定义即可判断.


2.【答案】D


【解析】根据线段、射线、直线的定义即可判断.


3.【答案】D


【解析】根据线段、射线、直线的定义查找.


4.【答案】D


【解析】可以交于1点；也可以构成四边形的形式，4个交点；也可以三条线形成三角形，第4条直线截其中两条直线，6个交点.


5.【答案】A


【解析】BA=BC-AC.


6.【答案】B


【解析】因为AB=CD,所以AC=BD，又因为BC=2AC，所以2AC=2BD=CB


所以3AC=CD.


7.【答案】D


【解析】C表示的数可能是-1或3，因此AC长可能是2或6.


8.【答案】D


【解析】由于点的位置不固定，因此会有许多种可能.



































巩固








1.如图，经过刨平的木板上的两个点，能弹出一条笔直的墨线，而且只能弹出一条墨线，能解释这一实际应用的数学知识是（ ）





A.两点确定一条直线 B.两点之间线段最短


C.垂线段最短 D.在同一平面内，过一点有且只有一条直线与已知直线垂直


2.如图，是学校花圃的一角，有的同学为了省时间图方便，在花圃中踩出了一条“捷径”，“捷径”的数学道理是（ ）．





A．两点确定一条直线 B．两点之间线段最短


C．垂线段最短 D．两点之间直线最短


3.如图，C、D是线段AB上两点，若CB＝5cm，DB=9cm，且D是AC的中点，则AC的长等于（ ）





A．6cm B．9cm C．8cm D．13cm


4.点C在线段AB上，下列条件中不能确定点C是线段AB中点的是（ ）


A. AC =BC B. AC +BC= AB C. AB =2AC D. BC =AB


5.如图，计划把河水引到水池中，先作，垂足为点，然后沿开渠，能使所开的渠道最短，这样设计的依据是 ．











6.如图，已知点A、B、C是数轴上三点，点C表示的数为6，BC＝4，AB＝12．


B


A


O


0


C


6





（1）数轴上点A表示的数是 ，点B表示的数是 ；


（2）动点P、Q同时从A、C出发，点P以每秒6个单位长度的速度沿数轴向右匀速运动，点Q以3个单位长度的速度沿数轴向左匀速运动，M为AP的中点， N在线段CQ上，且，设运动时间为t（t>0）秒．


①求数轴上点M、N表示的数（用含t的式子表示）；


②t为何值时，原点O恰为线段PQ的中点．





答案与解析


1.【答案】A


【解析】.两点确定一条直线


2.【答案】B


【解析】两点之间线段最短


3.【答案】C


【解析】因为CB=5，DB=9，所以CD=4，又因为点D是线段AB的中点.所以AC=2CD=8.


4.【答案】B


【解析】B选项确定的是C是中点.


5.【答案】B


【解析】直线外一点到已知直线垂线段最短


6.【答案】（1）;（2）见解析


【解析】（1）.


点表示的数;点表示的数;




















拔高








1.由绵阳出发到成都的某一次列车，运行途中须停靠的车站依次是：绵阳→罗江→黄许→德阳→广汉→清白江→新都→成都．那么要为这次列车制作的车票一共有（ ）


A.7种 B.8种 C.56种 D.28种


2.如图，已知点O在线段AB上，点C、D分别是AO、BO的中点





（1）AO= CO；BO= DO；


（2）若CO=3cm，DO=2cm，求线段AB的长度；


3.（1）如图，已知点C在线段AB上，且AC＝6cm，BC＝4cm，点M、N分别是AC、BC的中点，求线段MN的长度.


（2）若点C是线段AB上任意一点，且AC＝a，BC＝b，点M、N分别是AC、BC的中点，请直接写出线段MN的长度；（用含a、b的代数式表示）


（3）在（2）中，把点C是线段AB上任意一点改为：点C是直线AB上任意一点，其它条件不变，请求出线段MN的长度.（用含a、b的代数式表示）








答案与解析


1.【答案】D


【解析】7+6+5+4+3+2+1=28.


2.【答案】（1）2；2；（2）AB=10cm；


【解析】（1）根据中点的性质可得；


（2）AB=（3+2）×2=10cm.


3.【答案】见解析


【解析】（1）∵AC=6cm，点M是AC的中点


∴CM=AC=3cm


∵BC=4cm，点N是BC的中点


∴CN=BC=2cm


∴MN=CM+CN=5cm


∴线段MN的长度为5cm．


（2）MN=


（3）线段MN的长度会变化．


当点C在线段AB上时，由（2）知MN=


当点C在线段AB的延长线时，如图：





则AC=a＞BC=b


∵AC=a点M是AC的中点


∴CM=AC=a


∵BC=b点N是BC的中点


∴CN=BC=b


∴MN=CM﹣CN=


当点C在线段BA的延长线时，如图：





则AC=a＜BC=b


同理可求：CM=AC=a


CN=BC=b


∴MN=CN﹣CM=


∴综上所述，线段MN的长度会变化





七 、教学反思











.适用学科
初中数学
适用年级
初一
适用区域
北师版区域
课时时长（分钟）
120
知识点
1、线段、射线、直线的概念 5、线段的大小比较


2、线段、射线、直线的表示方法 6、线段的中点的定义


3、两点一线的应用 7、线段的中点的应用


4、平面图形的找规律问题 8、利用线段的性质说明点的位置
教学目标
1、知识目标．使学生在了解直线概念的基础上，理解射线和线段的概念，并能理解它们的区别与联系．


2、使学生在理解线段概念的基础上，了解线段的长度可以用正数来表示，因而线段可以度量、比较大小以及进行一些运算.使学生对几何图形与数之间的联系有一定的认识，从而初步了解数形结合的思想.


3、使学生学会线段的两种比较方法及表示法.
教学重点
1、直线、射线、线段的概念．


2、对线段与数之间的关系的认识，掌握线段比较的正确方法.
教学难点
1、对直线的“无限延伸”性的理解．


2、对线段与数之间的关系的认识，掌握线段比较的正确方法.