

初中数学北师大版七年级上册5.3 应用一元一次方程——水箱变高了教学设计
展开第15讲
讲
应用一元一次方程(一)
.
概 述
【教学建议】
本讲是初中方程应用题知识的开端,在学习本讲时,要注意让学生熟练掌握各种公式的应用,以便于更好的解决方程的应用题.
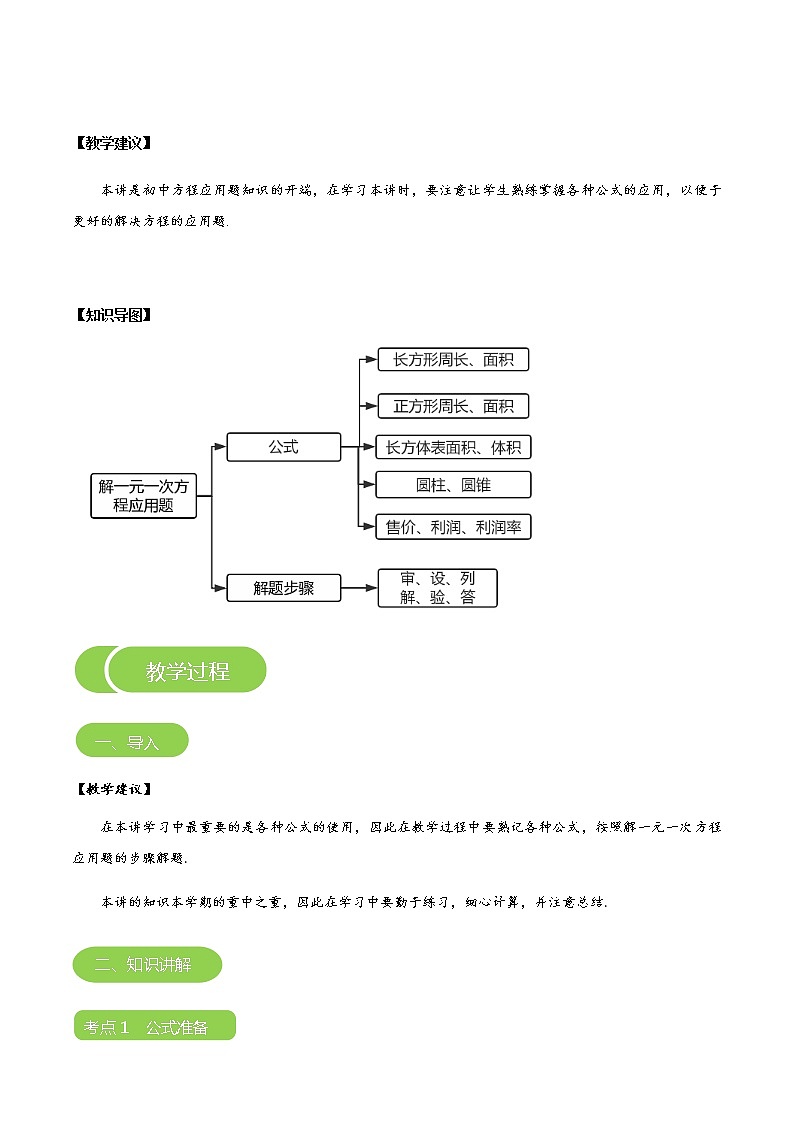
【知识导图】
教学过程
一、导入
【教学建议】
在本讲学习中最重要的是各种公式的使用,因此在教学过程中要熟记各种公式,按照解一元一次方程应用题的步骤解题.
本讲的知识本学期的重中之重,因此在学习中要勤于练习,细心计算,并注意总结.
二、知识讲解
考点1 公式准备
长方形的周长=(长+宽)×2;长方形的面积=长×宽;
正方形的周长=边长×4;正方形的面积=边长×边长;
长方体的体积=长×宽×高=底面积×高;
圆柱的体积=底面积×高.
售价=标价×折扣;利润=售价-成本(或进价);
利润率=利润÷成本×100%.
考点2 解一元一次方程应用题的步骤
①审:搞清题目中每一个已知量与未知量的含义;
②设:设未知数;
③列:找出等量关系、列出方程;
④解:解出方程;
⑤验:检验;
⑥答:作答.
三 、例题精析
类型一 周长与面积
例题1
如图所示,地面上钉着用一根彩绳围成的直角三角形,如果将直角三角形锐角顶点的一个钉子去掉,并将这根彩绳钉成一个长方形,则所钉长方形的长、宽各是多少?面积是多少?
【解析】三角形的周长=6+8+10=24,
①当去掉顶点A的钉子时,BC为长方形的一条边长,
设长方形的宽为x,
由题意得,2(x+6)=24,
解得:x=6,
则该长方形的长和宽均为6,
面积为:6×6=36;
②当去掉顶点B的钉子时,AC为长方形的一条边长,
设长方形的宽为x,
由题意得,2(x+8)=24, 解得:x=4,
则该长方形的长和宽8,4,
面积为:8×4=32.
答:长方形的长、宽、面积分别为6,6,36,或者为8,4,32.
【总结与反思】根据长方形的周长面积公式来计算.
类型二 等体积变形
例题1
一个棱长为8cm的正方体玻璃容器内有6cm高的纯净水,把它全部倒入底面积40cm2,高是12厘米的圆柱形容器里,这时水面高为多少厘米?
【解析】设这时水面高为xcm.根据题意,得
8×8×6=40x,解这个方程,得x=9.6
所以这时水面高为9.6cm.
【总结与反思】 形状变化,体积不变.
类型三 销售问题
例题1
某校七年级社会实践小组去商场调查商品销售情况,了解到该商场以每件80元的价格购进了某品牌衬衫500件, 并以每件120元的价格销售了400件.商场准备采取促销措施,将剩下的衬衫降价销售.请你帮商场计算一下,每件衬衫降价多少元时,销售完这批衬衫正好达到盈利45%的预期目标?
【解析】设每件衬衫降价x元,依题意有
120×400+(120-x)×100=80×500×(1+45%),
解得x=20.
答:每件衬衫降价20元时,销售完这批衬衫正好达到盈利45%的预期目标.
【总结与反思】根据题意即可列出方程求解
例题1
例题1
类型四 储蓄问题
一年期定期储蓄年利率为2.25%,所得利息交纳20%的利息税,已知某储户的一笔一年期定期储蓄到期纳税后得利息450元,问该储户存入多少本金?
【解析】设该储户存入x元,根据题意得:
2.25%x×(1−20%)=450,
解得:x=25000(元).
答:储户存入本金25000元。
【总结与反思】 根据题意即可列出方程求解.
类型五 选择购物方案
例题1
甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过1000元后,超出1000元的部分按90%收费;在乙商场累计购物超过500元后,超出500元的部分按95%收费,设小红在同一商场累计购物x元,其中x>100.
(1)根据题题意,填写下表(单位:元)
(2)当x取何值时,小红在甲、乙两商场的实际花费相同?
(3)当小红在同一商场累计购物超过1000元时,在哪家商场的实际花费少?
【解析】 (1)在甲商场:1000+(1300﹣1000)×0.9=1270,
1000+(2900﹣1000)×0.9=2710,
1000+(x﹣1000)×0.9=0.9x+100;
在乙商场:500+(1300﹣500)×0.95=1260,
500+(2900﹣500)×0.95=2780,
500+(x﹣500)×0.95=0.95x+25;
填表如下:
(2)根据题意得出:
0.9x+100=0.95x+25,
解得:x=1500,
答:当x为1500时,小红在甲、乙两商场的实际花费相同;
(3)当小红累计购物大于1500时,选择甲商场实际花费少;
当累计购物正好为1500元时,两商场花费相同;
当小红累计购物超过1000元而不到1500元时,在乙商场实际花费少.
答:当小红累计购物超过1000元而不到1500元时,在乙商场实际花费少;正好为1500元时,两商场花费相同;大于1500时,选择甲商场实际花费少.
【总结与反思】 根据题意即可列出方程求解.
四 、课堂运用
基础
1.用7.8米长的铁丝做成一个长方形框架,使长比宽多1.2米,求这个长方形框架的宽是多少米?设长方形的宽是x米,可列方程为( ).
A.x+(x+1.2)=7.8B.x+(x-1.2)=7.8
C.2[x+(x+1.2)]=7.8D.2[x+(x-1.2)]=7.8
2.某商店把一商品按标价的九折出售(即优惠10%),仍可获利20%,若该商品的标价为每件28元,则该商品的进价为( )
A.21元 B.19.8元 C.22.4元 D.25.2元
3.某种商品的进价为800元,标价为1200元,由于该商品积压,商店准备打折销售,但要保证利润率不低于20%,则最低可打( )
A.8折 B.8.5折 C.7折 D.6折学
4.小刚的爸爸前年买了某公司的二年期债券4500元,今年到期,扣除利息税后,共得本利和约4700元,问这种债券的年利率是________(精确到0.01%).
5.如图所示是用铁丝围成的一个梯形,将其改成一个长和宽比为2∶1的长方形,那么该长方形的长和宽分别为多少?
6.两个长方形的长与宽的比都是2:1,大长方形的宽比小长方形的宽多3cm,大长方形的周长是小长方形周长的2倍,求这两个长方形的面积.
答案与解析
1.【答案】C
【解析】根据长方形的周长公式列方程即可.长方形的周长=2×(长+宽),
故可列方程为2[x+(x+1.2)]=7.8.
2.【答案】A
【解析】设该商品的进价是x元.则实际售价为(1+20%)x.又实际售价为28×(1﹣10%),所以(1+20%)x=28×(1﹣10%),解得:x=21.
3.【答案】A
【解析】根据题意可得:1200·-800=800×20%,解得:x=8,即最低可打八折.
4.【答案】见解析
【解析】设长方形的宽为x,则长为2x.
由题意,得2(x+2x)=5+6+9+13,
解这个方程,得x=5.5,所以2x=11.
答:该长方形的长和宽分别为11,5.5.
5.【答案】见解析
【解析】设这种债券的年利率为x,由题意得:
4500+2×4500x=4700,
解得:x≈2.22%.
故答案为:2.22%.
6.【答案】见解析
【解析】设小长方形的宽为xcm,则小长方形的长为2xcm,大长方形的宽为(x+3)cm,大长方形的长为2(x+3)cm,根据题意得:
2[x+3+2(x+3)]=2×2(x+2x),
解得:x=3,
则小长方形的面积为2×3×3=18(cm2);
大长方形的面积为2×(3+3)×(3×3)=72(cm2).
巩固
1.一家商店将某种商品按进货价提高100%后,又以6折优惠售出,售价为60元,则这种商品的进货价是( )
A.120元 B.100元 C.72元 D.50元
2.某商品进价10元,标价15元,为了促销,现决定打折销售,但每件利润不少于2元,则最多打几折销售( ).
A.6折 B.7折 C.8折 D.9折
3.某商店有两个进价不同的计算器都卖了135元,其中一个盈利25%,另一个亏本25%,在这次买卖中,这家商店( )
A.不赔不赚 B.赚了9元 C.赚了18元 D.赔了18元
4.利息税的计算方法是:利息税=利息×20%.某储户按一年定期存款一笔,年利率2.25%,一年后取出时,扣除了利息税90元,据此分析,这笔存款的到期利息是____元,本金是_______元,银行向储户支付的现金是________元.
5.有一位工人师傅要锻造底面直径为40 cm的“矮胖”形圆柱,可他手上只有底面直径是10 cm,高为80 cm的“瘦长”形圆柱,试帮助这位师傅求出“矮胖”形圆柱的高.
6.惠民超市第一天以每件10元的价格购进某品牌茶杯15个,由于此种品牌商品价格看涨,第二天又以每件12元的价格购进同种茶杯35个,然后以相同的价格卖出,商店在销售这些茶杯时,要想利润率不低于10%,你觉得该如何定价?
7.现在,友谊商场进行促销活动,出售一种优惠购物卡(注:此卡只作为购物优惠凭证不能顶替货款),花300元买这种卡后,凭卡可在这家商场按标价的8折购物.
(1)顾客购买多少元金额的商品时,买卡与不买卡花钱相等?在什么情况下购物合算?
(2)小张要买一台标价为3500元的冰箱,如何购买合算?小张能节省多少元钱?
(3)小张按合算的方案,把这台冰箱买下,如果友谊商场还能盈利25%,这台冰箱的进价是多少元?
答案与解析
1.【答案】D
【解析】设进货价为x元,由题意得:
(1+100%)x•60%=60,
解得:x=50,
故选D.
2.【答案】C
【解析】设打x折销售,由题意得,解得x=8,所以最多打8折销售.
3.【答案】D
【解析】设盈利的这件成本为x元,则135-x=25%x,解得:x=108元;亏本的这件成本为y元,则y-135=25%y,解得:y=180元,则135×2-(108+180)=-18元,即赔了18元。
4.【答案】见解析
【解析】设这笔存款的到期利息是x元,
由题意得:20%x=90,
解得:x=450,
设这笔存款的本金是y元,根据题意得:
y⋅2.25%×20%=90,
解得:y=20000,
银行向储户支付的现金是20000(1+2.25%)−90=20360(元);
答:这笔存款的到期利息是450元,本金是20000元,银行向储户支付的现金是20360元。
故答案为:450,20000,20360.
5.【答案】见解析
【解析】设锻造成“矮胖”形圆柱的高为x cm,
根据题意,得
π·52·80=π·202·x.
解这个方程,得
x=5.
答:“矮胖”形圆柱的高为5 cm.
6.【答案】见解析
【解析】设每个茶杯的最低售价为x元,由题意,得
15(x-10)+35(x-12)=(15×10+35×12)×10%,
解得x=12.54.
答:商店在销售这些茶杯时每个茶杯的售价不能低于12.54元.
7.【答案】见解析
【解析】(1)设顾客购买元金额的商品时,买卡与不买卡花钱相等.
依题意:,
解得:,
所以:当顾客消费小于1500元时,不买卡合算.
当顾客消费等于1500元时,买卡与不买花钱卡相等.
当顾客消费大于1500元时,买卡合算.
(2)因为3500>1500,所以买卡合算,,
答:小张买卡合算,买卡可以节省400元.
(3)设这台冰箱的进价为元,依题意:,
解得:(元),
答:这台冰箱的进价是2480元.
拔高
1. 把一根长12cm的铁丝按要求围成图形:
(1)围成一个长比宽多2cm的长方形,求长和宽各是多少?
(2)围成一个正方形,此时正方形的边长是多少?它所围成的面积较(1)中有何变化?
(3)围成一个圆,此时圆的半径是多少?它所围成的面积较(2)中又有何变化?(π取3.14)
(4)如果让你负责设计高度一定、底面周长一定的饮料包装盒,为了使饮料盛的最多,你会将底面设计成什么图形?并解释你的理由.
2.某班将买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍.乒乓球拍每副定价30元,乒乓球每盒定价5元,经洽谈后,甲店每买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠.该班需球拍5副,乒乓球若干盒(不小于5盒).问:
(1)当购买乒乓球多少盒时,两种优惠办法付款一样?
(2)当购买15盒、30盒乒乓球时,请你去办这件事,你打算去哪家商店购买?为什么?
答案与解析
1.【答案】见解析
【解析】(1)设这时长方形的宽为xcm,则长为(x+2)cm,
根据题意得出:
2[(x+2)+x]=12,
解得:x=2,则2+2=4,
答:长和宽各是4cm,2cm;
(2)设这时正方形的边长为ycm,根据题意得出:
4y=12,
解得:y=3,
则正方形面积为:3×3=9(cm2),
答:正方形的边长为3cm,它所围成的面积为9cm2,
∵(1)中长方形面积为4×2=8(cm2),
∴这时正方形的面积比(1)中的面积增大1cm2;
(3)设圆的半径为acm,根据题意得出:2×3.14×a=12,
解得:a=,
∴圆的半径为:cm,则它围成的面积为:3.14×()2=(cm2),
此时比(2)中的面积增大:-9=(cm2);
(4)应将底面积设计成圆形,因为在高度和底面周长一定时,底面积最大,容积也就最大.
2.【答案】见解析
【解析】(1)甲店:30×5+5×(x﹣5)=5x+125(元)
乙店:90%(30×5+5x)=4.5x+135(元);
(2)5x+125=4.5x+135,解得:x=20;
(3)当购买15盒乒乓球时,
若在甲店购买,则费用是:5×15+125=200元,
若在乙店购买,则费用是:4.5×15+135=202.5元.
则应该在甲店购买;
当购买30盒乒乓球时,
若在甲店购买,则费用是:30×5+125=275元,
若在乙店购买,则费用是:30×4.5+135=270元,
应该在乙店购买.
答:当购买乒乓球20盒时,在甲、乙两店所需支付的费用一样;当购买15盒乒乓球时,应该在甲店购买;当购买30盒乒乓球时,应该在乙店购买.
五 、课堂小结
一、公式
长方形的周长=(长+宽)×2;长方形的面积=长×宽;
正方形的周长=边长×4;正方形的面积=边长×边长;
长方体的体积=长×宽×高=底面积×高;
圆柱的体积=底面积×高.
售价=标价×折扣;利润=售价-成本(或进价);
利润率=利润÷成本×100%.
二、解一元一次方程应用题的一般步骤
①审:搞清题目中每一个已知量与未知量的含义;
②设:设未知数;
③列:找出等量关系、列出方程;
④解:解出方程;
⑤验:检验;
⑥答:作答.
六 、课后作业
基础
1.一根铁丝用去后,还剩下10m,这根铁丝原来的长是多少米?如果设这根铁丝原来的长是xm,那么列出的方程是( )
A.x-=10
B.x-10=
C.x-=10
D.x=10
2.小王去早市为餐馆选购蔬菜,他指着标价为每斤3元的豆角问摊主:“这豆角能便宜吗?”摊主:“多买按八折,你要多少斤?”小王报了数量后摊主同意按八折卖给小王,并说:“之前一人只比你少买5斤就是按标价,还比你多花了3元呢!”小王购买豆角的数量是( )
A.25斤 B.20斤 C.30斤 D.15斤
3.某品牌手机的进价为1200元,按原价的八折出售可获利14%,则该手机的原售价为( )
A.1800元 B.1700元 C.1710元 D.1750元
4. 国家规定存款利息的纳税办法是:利息税=利息×20%,储户取款时由银行代扣代收。若银行一年 定期储蓄的年利率为2.25%,其储户取出一年到期的本金及利息时,扣除了利息税36元,则银行向该储户支付的现金是______元.
5. 一个长方形的养鸡场的长边靠墙(墙长14米),其他三边用篱笆围成,现有35米长的篱笆,小李打算用它围成一个鸡场,其中长比宽多5米;小张设计成长比宽多2米,你认为谁的设计更符合实际?此时鸡场的面积是多少?
6. 有一个底面直径为0.2m得圆柱形水桶,把936g重的钢球全部浸没在水中,如果取出钢球,那么液面下降多少厘米?(1立方厘米钢重7.8g,π取3.14,结果精确到0.01cm)
7. 用一底面为15cm×15cm的长方体容器装满水,向一个长,宽,高分别为20cm,15cm,10cm的长方体铁盒内倒水,当铁盒装满时,长方体容器中的水面下降了多少厘米?(用一元一次方程解)
8.七年级(5)班开展“我的中国梦“主题班会活动,需要制作一个“梦之盒”,用来装同学们的卡片,图1是边长为30cm的正方形纸板,裁掉阴影部分后将其折叠成如图2所示的长方体盒子,已知该长方体的宽是高的2倍,则它的体积是多少cm3?
9.某顾客在商场看中了甲、乙两种冰箱,其中甲冰箱的价格为2100元,日均耗电量为1度;乙冰箱是新节能产品,价格为2220元,日均耗电量为0.5度.若这两种冰箱的效果相同且甲冰箱可以打折但乙冰箱不打折,请你就价格方面计算说明,甲冰箱至少打几折时购买比较合算?(假设:每度电0.5元,两种冰箱的使用寿命均为10年,平均每年使用300天.)
10.李明以两种形式储蓄了500元钱,一种储蓄年利率是5%,另一种是4%,一年后共得利息23元5角,两种储蓄各存了多少钱 (不用纳利息税) ?
11.某学校班主任暑假带领该班三好学生去旅游,甲旅行社说:“如果教师买全票一张,其余学生享受半价优惠”;乙旅行社说:“教师在内全部按票价的6折优惠”;若全票价格是240元/张.
(1)如果有10名学生,应选择哪个旅行社,并说出理由;
(2)当学生人数是多少时,两家旅行社收费一样多.
答案与解析
1.【答案】C
【解析】设这根铁丝原来的长是x m
x-(3/5)x=10
故本题选择C
2.【答案】C
【解析】设小王购买豆角的数量是x斤,则3×80%x=3(x-5)-3,
整理,得2.4x=3x-18,
解得 x=30.
即小王购买豆角的数量是30斤.
3.【答案】C
【解析】设手机的原售价为x元,
由题意得,0.8x-1200=1200×14%,
解得:x=1710.
即该手机的售价为1710元.
4.【答案】见解析
【解析】本金为:36÷2.25%÷20%,=36÷0.0225÷0.2,=8000(元);
银行向该储户支付现金为:
8000×(1+2.25%)−36,=8000×1.0225−36,=8180−36,=8144(元).
答:银行付给该储户支付的现金是8144元。
5.【答案】见解析
【解析】设养鸡场的宽为xm,按小李的设计,则长为(x+5)m,
则有2x+x+5=35,x=10,则长为15m,而墙长14m,这样的设计不符合实际情况,
按小张的设计,长为(x+2)m,则有2x+x+2=35,x=11,则长为13m<14m,
故此时鸡场面积是13×11=143(m2),
答:小张的设计符合实际,此时鸡场面积是143m2。
6.【答案】见解析
【解析】设液面下降了x cm,根据题意,得π·x=.
解方程,得x≈0.38
答:液面下降了约0.38cm.
7.【答案】见解析
【解析】设长方体水面下降x厘米
15×15×x=20×15×10
解得x=
答:长方体容器中的水面下降了厘米.
8.【答案】见解析
【解析】长方体的高为xcm,然后表示出其宽为,
根据题意得:15−x=2x,
解得:x=5,
故长方体的宽为10cm,长为20cm,
则长方体的体积为5×10×20=1000cm3.
9.【答案】见解析
【解析】设甲冰箱至少打x折时购买甲冰箱比较合算,
由题意得,2100×+10×300×1×0.5=2220+10×300×0.5×0.5,
解得:x=7.
答:甲冰箱至少打7折时购买甲冰箱比较合算.
10.【答案】见解析
【解析】设年利率是5%的储蓄存了x元,则年利率是4%的储蓄了(500-x)元。
x×5%+(500-X)×4%=23.5
0.05x+20-0.04x=23.5
20+0.01x=23.5
0.01x=23.5-20
0.01x=3.5
x=350
∴500-350=150
答:年利率是5%和4%的两种储蓄分别存了350元和150元
11.【答案】见解析
【解析】(1)有10名学生时,
甲旅行社的费用为:240+240×0.5×10=1440元;
乙旅行社的费用为:240×0.6×(10+1)=1584元>1440元 ,
所以应参加甲旅行社.
(2)设有x名学生,根据题意得:
240+240×0.5x=240×0.6×(x+1),
解之,得:x=4,
答:当学生人数是4时,两家旅行社收费一样多.
巩固
1.一家商店把某商品按标价的九折出售仍可获利15%,若该商品的进价是35元,若设标价为x元,则可列得方程( )
A. B.
C. D.
2.某文化商场,同时卖出两台电子琴,每台均卖960元,以成本计算,第一台盈利20%,另一台亏本20%,则本次出售中,商场( )。
A.不盈不亏 B.盈利160元 C.盈利80元 D.亏本80元
3.某商人在一次买卖中均以120元卖出两件不同的衣服,一件赚25%,一件赔25%,则在这次交易中该商人的赚赔情况是( )
A.赚16元 B.赔16元 C.不赚不赔 D.无法确定
4.欣平超市推出如下优惠方案;
(1)一次性购物不超过100元不享受优惠;
(2)一次性购物超过100元但不超过300元一律九折;
(3)一次性购物超过300元一律八折.
王波两次购物分别付款80元、252元,如果王波一次性购买与上两次相同的商品,则应付款( )
A.288元
B.322元
C.288元或316元
D.332元或363元
5.将内直径为200mm的圆柱形水桶中的水倒入一个内部长,宽,高分别是300mm,300mm,80mm的长方形容器中,恰好倒满,试确定圆柱形水桶内水面的高度(取3.14,结果精确到1mm)
6. 一种圆筒状包装的保鲜膜,如图所示,其规格为20cm×60m,经测量这筒保鲜膜的内径Ф1,外径Ф2的长分别为3.2cm、4.0cm,则这种保鲜膜的厚度约为多少厘米?(π取3.14)
7.小张自主创业开了一家服装店,因为进货时没有进行市场调查,在换季时积压了一批服装,为了缓解资金的压力,小张决定打折销售.若每件服装按标价的五折出售将亏20元,若按标价的八折出售将赚40元.
(1)每件服装的标价是多少元?
(2)每件服装的成本价是多少元?
(3)为保证不亏本,你告诉小张最多能打几折?
8.王叔叔想用一笔钱买年利率为2.89%的3年期国库券,如果他想3年后的本息和为2万元,现在应买这种国库券多少?
9.在“十一”黄金周期间,小明、小亮等同学随家人一同到江郎山游玩,看见门口有如下票价提示:“成人:35元/张;学生:按成人票5折优惠;团体票(16人以上含16人):按成人票价六折优惠”。
在购买门票时,小明与他爸爸有如下对话,爸爸:“大人门票每张35元,学生门票对折优惠,我们共有12人,共需350元”。小明:“爸爸,等一下,让我算一算,换一种方式买票是不是可以更省钱”。
问题:(1)小明他们一共去了几个成人,几个学生?
(2)请你帮小明算一算,用哪种方式买票更省钱?说明理由
答案与解析
1.【答案】A
【解析】获利=(售价-进价)÷进价,根据题意可得:=15%.
2.【答案】D
【解析】设两台电子琴的原价分别为x与y,
则第一台可列方程(1+20%)•x=960,解得:x=800.
比较可知,第一台赚了160元,
第二台可列方程(1-20%)•y=960,解得:y=1200元,
比较可知第二台亏了240元,
两台一合则赔了80元.
3.【答案】B
【解析】设赚了25%的衣服的进价是m元,则(1+25%)m=120,解得m=96元,则实际赚了96×25%=24元;
设赔了25%的衣服的进价是n元,则(1-25%)n=120,解得n=160元,则赔了160-120=40元;
∵40>24;∴赔大于赚,在这次交易中,该商人是赔了40-24=16元.故选B.
4.【答案】C
【解析】(1)第一次购物显然没有超过100,
即在第二次消费80元的情况下,他的实质购物价值只能是80元.
(2)第二次购物消费252元,则可能有两种情况,这两种情况下付款方式不同(折扣率不同):
①第一种情况:他消费超过100元但不足300元,这时候他是按照9折付款的.
设第二次实质购物价值为x,那么依题意有x×0.9=252,解得:x=280.
①第二种情况:他消费超过300元,这时候他是按照8折付款的.
设第二次实质购物价值为x,那么依题意有x×0.8=252,解得:x=315.
即在第二次消费252元的情况下,他的实际购物价值可能是280元或315元.
综上所述,他两次购物的实质价值为80+280=360或80+315=395,均超过了300元.因此均可以按照8折付款:
360×0.8=288元
395×0.8=316元
故填288元或316元.故选C.
5.【答案】见解析
【解析】设圆柱形的水桶的水高为xmm
1002·3.14·x=300×300×80
31400x=7200000
x≈229
答:圆柱形的水桶的水高为229mm.
6.【答案】见解析
【解析】设这种保鲜膜得厚度为xcm.
根据题意,得:
解得:x≈0.00075
答:这种保鲜膜的厚度约为0.00075厘米.
7.【答案】见解析
【解析】(1)设标价是x元,由题意得:50%x+20=80%x-40,
解得x=200元,
答:每件服装的标价是200元;
每件服装的成本价是50%x+20=120元;
答:每件服装的成本价是120元
(3)120÷200=0.6
答:最多能打6折.
8.【答案】见解析
【解析】设现在应买这种国库券x元。
x+2.89%×3x=20000
1.0867x=20000
x≈18405
答:现在应买这种国库券18405元。
9.【答案】见解析
【解析】(1)设一共去了x个成年人,则学生有12-x人,根据大人门票每张35元,学生门票对折优惠,共需350元,即可列方程求解.
(2)计算出购买团体票时的费用,与350元比较即可.
试题解析:(1)设一共去了x个成年人,
根据题意,列方程得35x+35×(12-x)=350,
解得x=8,学生得人数为12-8=4人,
所以,一共去了8个成人,4个学生.
(2)如果买团体票需要花费16×35×60%=336(元),
因为336<350,所以买团体票更省钱.
拔高
1.有一种用来画圆的工具板(如图所示),工具板长21cm,上面依次排列着大小不等的五个圆(孔),其中最大圆的直径为3cm,其余圆的直径从左到右依次递减0.2cm.最大圆的左侧距工具板左侧边缘1.5cm,最小圆的右侧距工具板右侧边缘1.5cm,相邻两圆的间距d均相等。
(1)直接写出其余四个圆的直径长;
(2)求相邻两圆的间距。
2. 如图,在水平桌面上有甲、乙两个内部呈圆柱形的容器,内部底面积分别为80cm2、100cm2,且甲容器装满水,乙容器是空的。若将甲中的水全部倒入乙中,则乙中的水位高度比原先甲的水位高度低了8cm,求甲的容积为何?
3.某书店开展学生优惠售书活动,凡一次性购书不超过200元的一律九折优惠,超过200元的,其中200元按九折计算,超过200元的部分按八折优惠,某学生第一次去购书付款72元,第二次去购书享受八折优惠,他查看了买书的定价,发现两次共节省34元,求学生第二次购书实际付了多少元。
4.情景:
试根据图中信息,解答下列问题:
(1)购买8根跳绳需 元,购买14根跳绳需 元;
(2)小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.
答案与解析
1.【答案】见解析
【解析】(1)其余四个圆的直径依次为:2.8cm,2.6cm,2.4cm,2.2cm.
(2)设两圆的距离是d,
4d+1.5+1.5+3+2.8+2.6+2.4+2.2=21
4d+16=21
d=54
故相邻两圆的间距为54cm.
2.【答案】见解析
【解析】设甲的容积为x,
则甲的高度为:(x÷80)cm,
乙的高度为:(x÷100)cm,
根据题中等量关系可列出方程式:(x÷80)−(x÷100)=8,
解得:x=3200,
所以甲的容积为3200cm2.
3.【答案】见解析
【解析】第二次优惠:
34−72÷90%×(1−90%),=34−8,=26(元);
设第二次购书原价x元,
200×90%+(x−200)×80%=x−26,
解得:x=230,
实际购书价:230−26=204元;
答:第二次购书实际付了204元。
4.【答案】见解析
【解析】(1)25×8=200元;25×14×0.8=280元.
设小红购买跳绳x根,则25×0.8x=25(x﹣2)﹣5,解得x=11,
(3)故有这种可能,小红购买跳绳11根.
七 、教学反思
.适用学科
初中数学
适用年级
初一
适用区域
北师版区域
课时时长(分钟)
120
知识点
1、周长与面积
2、等积变形
3、销售问题
4、储蓄问题
5、选择购物方案
教学目标
1、通过具体问题的解决,体会利用方程解决问题的关键是寻找等量关系.
2、理解售价、标价、利润、利润率、成本等概念及它们之间的关系式;
3、体验运用数学知识解决实际问题的过程,归纳出运用方程解决实际问题的一般步骤。
4、培养学生思考、探究、分析问题的能力。
教学重点
依据问题中的各种数量关系,寻找出等量关系,建立方程,并规范解题步骤.
教学难点
1、寻找图形问题中的等量关系,建立一元一次方程,使实际问题数学化.
2、分析打折销售中的各种数量关系,并根据关系式列出合理的方程.
累计购物
1300
2900
x
在甲商场花费
在乙商场花费
累计购物
1300
2900
x
在甲商场花费
1270
2710
0.9x+100
在乙商场花费
1260
2780
0.95x+25
北师大版七年级上册5.3 应用一元一次方程——水箱变高了教案及反思: 这是一份北师大版七年级上册5.3 应用一元一次方程——水箱变高了教案及反思,共39页。教案主要包含了教学建议,知识导图,总结与反思等内容,欢迎下载使用。
初中数学北师大版七年级上册3.3 整式教案及反思: 这是一份初中数学北师大版七年级上册3.3 整式教案及反思,共20页。教案主要包含了教学建议,知识导图,总结与反思等内容,欢迎下载使用。
初中北师大版3.2 代数式教学设计及反思: 这是一份初中北师大版3.2 代数式教学设计及反思,共19页。教案主要包含了教学建议,知识导图,总结与反思等内容,欢迎下载使用。













