初中数学人教版八年级上册12.2 三角形全等的判定教学设计

这是一份初中数学人教版八年级上册12.2 三角形全等的判定教学设计，共6页。教案主要包含了知识点与方法梳理，经典例题，经典练习，巩固练习等内容，欢迎下载使用。

【知识点与方法梳理】


复习巩固：


三角形全等的判定一（公理）：


三边对应相等的两个三角形全等，简写为“边边边”或“SSS”．


三角形全等的判定二（定理）：


有两边和它们的夹角对应相等的两个三角形全等(简称“边角边”或“SAS”)


新课要点：


三角形全等的判定三（定理）


两角和它们的夹边对应相等的两个三角形全等（可以简写成“角边角”或“ASA”）．


三角形全等的判定四（定理）


两个角和其中一角的对边对应相等的两个三角形全等（可以简写成“角角边”或“AAS”）．


【经典例题】


例1. 如图，四边形ABCD的对角线AC与BD相交于O点，


D


C


B


A


O


1


2


3


4


∠1＝∠2，∠3＝∠4．


求证：（1）△ABC≌△ADC；（2）BO＝DO．























例2.如图，∠DCE=90，CD=CE，AD⊥AC，BE⊥AC，垂足分别为A、B，试说明AD+AB＝BE.





























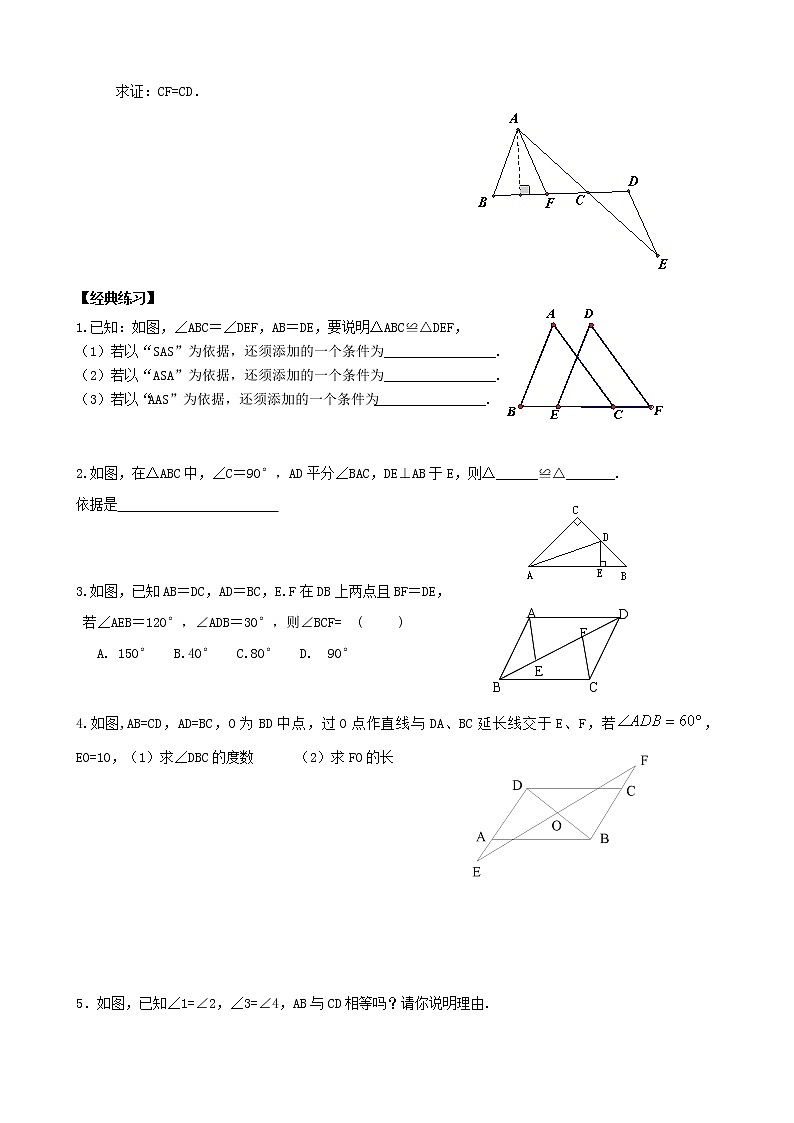
例3. 已知：如图，AB=DE，直线AE，BD相交于C，∠B＋∠D=180°，AF∥DE，交BD于F．


求证：CF=CD．























【经典练习】


1.已知：如图，∠ABC＝∠DEF，AB＝DE，要说明△ABC≌△DEF，


（1）若以“SAS”为依据，还须添加的一个条件为________________.


（2）若以“ASA”为依据，还须添加的一个条件为________________.


（3）若以“AAS”为依据，还须添加的一个条件为________________.








2.如图，在△ABC中，∠C＝90°，AD平分∠BAC，DE⊥AB于E，则△______≌△_______.


依据是








A


D


B


C


E


F





3.如图，已知AB＝DC，AD＝BC，E.F在DB上两点且BF＝DE，


若∠AEB＝120°，∠ADB＝30°，则∠BCF= ( )


A. 150° B.40° C.80° D. 90°





4.如图,AB=CD，AD=BC，O为BD中点，过O点作直线与DA、BC延长线交于E、F，若，EO=10，（1）求∠DBC的度数 （2）求FO的长





























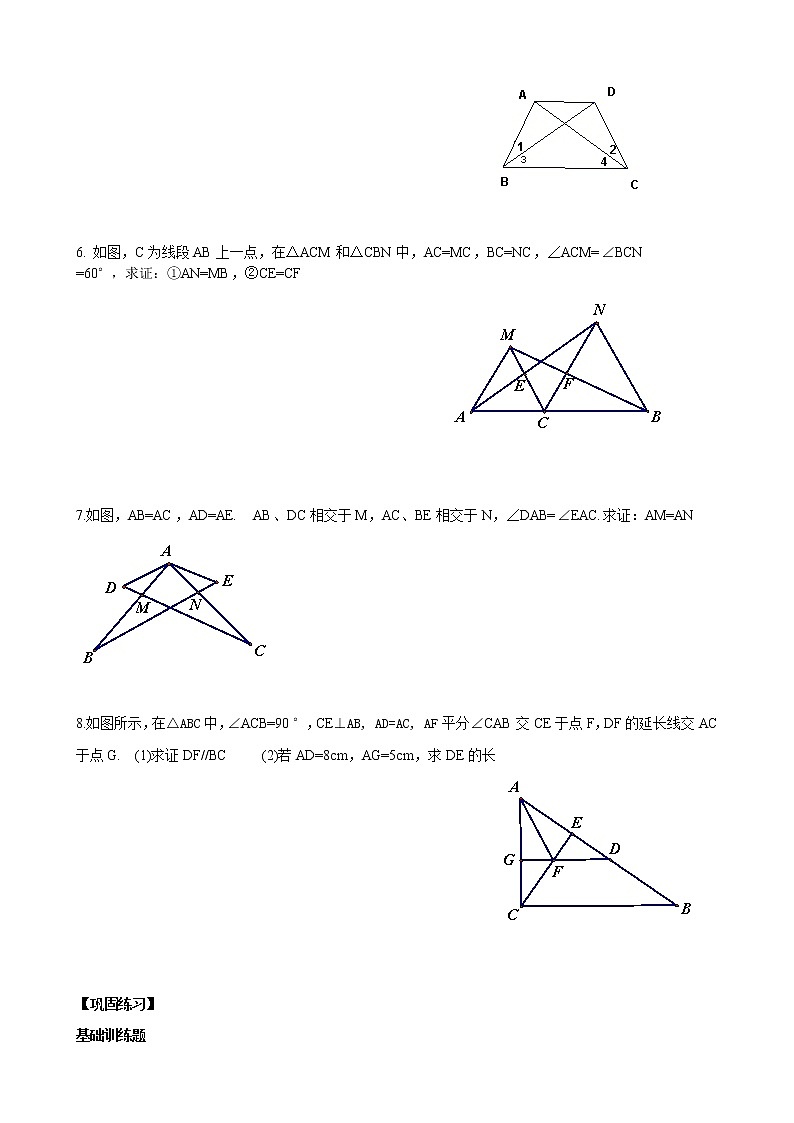
5．如图，已知∠1=∠2，∠3=∠4，AB与CD相等吗？请你说明理由.


























6. 如图，C为线段AB上一点，在△ACM和△CBN中，AC=MC，BC=NC，∠ACM=∠BCN


=60°，求证：①AN=MB，②CE=CF


























7.如图，AB=AC，AD=AE. AB、DC相交于M，AC、BE相交于N，∠DAB=∠EAC.求证：AM=AN








8.如图所示，在△ABC中，∠ACB=90°，CE⊥AB, AD=AC, AF平分∠CAB交CE于点F，DF的延长线交AC于点G. (1)求证DF//BC (2)若AD=8cm，AG=5cm，求DE的长























【巩固练习】


基础训练题


1.如图，AB∥CD，AD∥BC，那么AD=BC，AB=ＤC，你能说明其中的道理吗？(可添加辅助线)














2. 如图，AE⊥AB，AD⊥AC，AB=AC，∠B=∠C，求证：BD=CE。

















3.已知∠BAC=∠DAE，∠ABD=∠ACE，BD=CE.求证；AB=AC，AD=AE；











4.已知BE⊥AD，CF⊥AD，且BE=CF。判断AD是△ABC的中线还是角平分线？请说明理由。




















5. 如图，四边形ABCD中，AB∥DC，BE、CE分别平分∠ABC、∠BCD，且点E在AD上。求证：BC=AB+DC。






































6.已知：AB//ED，∠EAB=∠BDE，AF=CD，EF=BC，求证：∠F=∠C


D


C


B


A


F


E








能力提高题


1.已知如图，E.F在BD上，且AB＝CD，BF＝DE，AE＝CF,求证：AC与BD互相平分.


A


B


E


O


F


D


C





























B


A


C


D


F


2


1


E


2.已知：∠1=∠2，CD=DE，EF//AB，求证：EF=AC






































3.如图，已知∠1=∠2，∠3=∠4，求证：AD//BC





























4.已知：在△AOB和△COD中，OA=OB, OC=OD.


(1)如图1，若∠AOB=∠COD=60°，求证：①AC=BD; ②∠APB=60°。


(2)如图2，若∠AOB=∠COD=,则AC与BD是否相等？（直接回答，不用证明）


求此时的∠APB（用表示）






































5.如图9所示，△ABC是等腰直角三角形，∠ACB＝90°，AD是BC边上的中线，过C作AD的垂线，交AB于点E，交AD于点F，求证：∠ADC＝∠BDE．


A


B


C


D


E


F


图9


(提示:过C作CH垂直于AB,垂足为H,交AD于M)