2021年高考数学（理）突破性讲练之三角函数专题01 任意角的三角函数

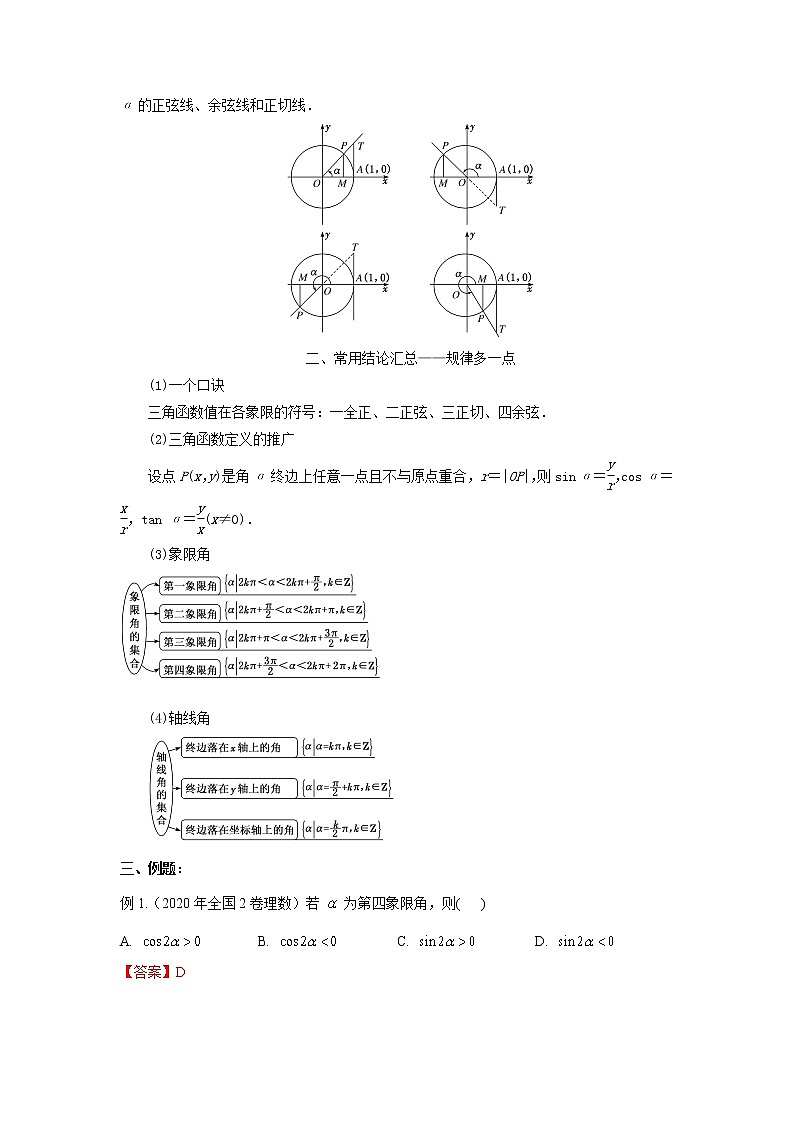
专题01 任意角的三角函数一、考点传真：1.了解任意角的概念和弧度制的概念；2.能进行弧度与角度的互化；3.理解任意角的三角函数(正弦、余弦、正切)的定义.二、知识的梳理：1．角的概念的推广(1)定义：角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形．(2)分类(3)终边相同的角：所有与角α终边相同的角，连同角α在内，可构成一个集合S＝{β|β＝α＋2kπ，k∈Z}．　　终边相同的角不一定相等，但相等的角其终边一定相同． 2．弧度制的定义和公式(1)定义：把长度等于半径长的弧所对的圆心角叫做1弧度的角，弧度记作rad.(2)公式：角α的弧度数公式|α|＝(l表示弧长)角度与弧度的换算①1°＝ rad；②1 rad＝°弧长公式l＝|α|r扇形面积公式S＝lr＝|α|r2 有关角度与弧度的两个注意点(1)角度与弧度的换算的关键是π＝180°，在同一个式子中，采用的度量制度必须一致，不可混用．(2)利用扇形的弧长和面积公式解题时，要注意角的单位必须是弧度．3．任意角的三角函数(1)定义：设α是一个任意角，它的终边与单位圆交于点P(x，y)，那么sin α＝，cos α＝，tan α＝(x≠0)．(2)几何表示：三角函数线可以看作是三角函数的几何表示．正弦线的起点都在x轴上，余弦线的起点都是原点，正切线的起点都是(1,0)．如图中有向线段MP，OM，AT分别叫做角α的正弦线、余弦线和正切线．二、常用结论汇总——规律多一点(1)一个口诀三角函数值在各象限的符号：一全正、二正弦、三正切、四余弦．(2)三角函数定义的推广设点P(x，y)是角α终边上任意一点且不与原点重合，r＝|OP|，则sin α＝，cos α＝，tan α＝(x≠0)．(3)象限角
 (4)轴线角三、例题：例1.（2020年全国2卷理数）若为第四象限角，则(   )A.  B.  C.  D. 【答案】D【解析】 由题意，知，所以，所以或，，故选D.优解 当时，，，排除A，B，C，故选D.例2.（2020年北京卷）2020年3月14日是全球首个国际圆周率日（π Day）.历史上，求圆周率π的方法有多种，与中国传统数学中的“割圆术”相似，数学家阿尔·卡西的方法是:当正整数n充分大时，计算单位圆的内接正边形的周长和外切正边形（各边均与圆相切的正边形）的周长，将它们的算术平均数作为的近似值，按照阿尔·卡西的方法，π的近似值的表达式是（   ）A. B.C.  D.【答案】B【解析】连接圆心与圆内接正边形的各顶点，则圆内接正边形被分割成个等腰三角形，每个等腰三角形的腰长均为圆的半径1，顶角均为，底角均为，所以等腰三角形的底边长均为，故单位圆的内接正边形的周长为；连接圆心与圆外切正边形的各顶点，则圆外切正边形被分割成个等腰三角形，每个等腰三角形底边上的高均为圆的半径1，顶角均为，顶角的一半均为，所以等腰三角形的底边长均为，故单位圆的外切正边形的周长为.因为单位圆的内接正边形的周长和外切正边形的周长的算术平均数为的近似值，所以，所以，故选A.例3. （2019北京卷）如图，A，B是半径为2的圆周上的定点，P为圆周上的动点，是锐角，大小为β.图中阴影区域的面积的最大值为（A）4β+4cosβ （B）4β+4sinβ （C）2β+2cosβ （D）2β+2sinβ【答案】B【解析】 由题意和题图可知，当为优弧的中点时，阴影部分的面积取最大值，如图所示，设圆心为，，.此时阴影部分面积.故选B.例4.(2018全国卷Ⅰ)已知角的顶点为坐标原点，始边与轴的非负半轴重合，终边上有两点，，且，则A．   B．    C．    D．【答案】B【解析】由题意知，因为，所以，，得，由题意知，所以．故选B．例5.(2018北京)在平面坐标系中，，，，是圆上的四段弧（如图），点在其中一段上，角以为始边，为终边，若，则所在的圆弧是A．      B．       C．   D． 【答案】C【解析】设点的坐标为，利用三角函数可得，所以，．所以所在的圆弧是，故选C．例6.（2017北京）在平面直角坐标系中，角与角均以Ox为始边，它们的终边关于y轴对称．若sin=，则sin=_________．【答案】【解析】与关于轴对称，则 ，所以．例7.（2018浙江）已知角的顶点与原点重合，始边与轴的非负半轴重合，它的终边过点．(1)求的值；(2)若角满足，求的值．【解析】(1)由角的终边过点得，所以．(2)由角的终边过点得，由得．由得，所以或．四、巩固练习：1．2弧度的角所在的象限是(　　)A．第一象限　　　　　　 B．第二象限C．第三象限  D．第四象限【答案】B　【解析】∵<2<π，∴2弧度的角在第二象限．2．(2019·长春普通高中一模)若角α的顶点为坐标原点，始边在x轴的非负半轴上，终边在直线y＝－x上，则角α的取值集合是(　　)A.B.C.D.【答案】D　【解析】因为直线y＝－x的倾斜角是，所以终边落在直线y＝－x上的角的取值集合为α.故选D.3．点P(cos 2 019°，sin 2 019°)所在的象限是(　　)A．第一象限  B．第二象限C．第三象限  D．第四象限【答案】C　【解析】2 019°＝5×360°＋219°，即角2 019°与角219°的终边相同，219°＝180°＋39°，所以角219°在第三象限，即角2 019°也在第三象限．所以cos 2 019°<0，sin 2 019°<0，所以点P在第三象限．4．已知角α的终边与单位圆交于点，则sin α的值为(　　)A．－  B．－C.   D.【答案】B　【解析】根据三角函数的定义，角α的终边与单位圆交点的纵坐标为角α的正弦值．5．半径为1 cm，圆心角为150°的角所对的弧长为(　　)A. cm   B. cmC. cm   D. cm【答案】D　【解析】∵α＝150°＝π rad，∴l＝α·r＝π cm.6．设θ是第三象限角，且＝－cos ，则是(　　)A．第一象限角  B．第二象限角C．第三象限角  D．第四象限角【答案】B　【解析】由θ是第三象限角，知为第二或第四象限角，∵＝－cos ，∴cos ≤0，综上知为第二象限角．7.设角α的顶点为坐标原点，始边为x轴的正半轴，则“α的终边在第一、二象限”是“sin α>0”的(　　)A．充分不必要条件  B．必要不充分条件C．充要条件  D．既不充分也不必要条件【答案】A　【解析】α的终边在第一、二象限能推出sin α>0，sin α>0成立能推出α的终边在第一、二象限或y轴的正半轴上，故“α的终边在第一、二象限”是“sin α>0”的充分不必要条件．故选A.8.已知角α(0°≤α<360°)终边上一点的坐标为(sin 150°，cos 150°)，则α＝(　　)A．150°  B．135°C．300°  D．60°【答案】C　【解析】sin 150°＝>0，cos 150°＝－<0，角α终边上一点的坐标为，故该点在第四象限，由三角函数的定义得sin α＝－，又0°≤α<360°，所以角α为300°，故选C.9．(2018·四川石室中学期中)已知角α的终边经过点(3，－4)，则sin α＋＝(　　)A．－   B.C.   D.【答案】D　【解析】∵角α的终边经过点(3，－4)，∴sin α＝－，cos α＝，∴sin α＋＝－＋＝.故选D.10．(2019·南昌二中模拟)已知角α终边上一点P的坐标是(2sin 2，－2cos 2)，则sin α等于(　　)A．sin 2  B．－sin 2C．cos 2  D．－cos 2【答案】D　【解析】因为r＝＝2，由任意角的三角函数的定义，得sin α＝＝－cos 2.11．已知角α＝2kπ－(k∈Z)，若角θ与角α的终边相同，则y＝＋＋的值为(　　)A．1  B．－1C．3  D．－3【答案】B　【解析】由α＝2kπ－(k∈Z)及终边相同的概念知，角α的终边在第四象限，又角θ与角α的终边相同，所以角θ是第四象限角，所以sin θ＜0，cos θ＞0，tan θ＜0.所以y＝－1＋1－1＝－1.12．(2019·洛阳阶段性测试)在平面直角坐标系xOy中，角α的顶点为坐标原点，始边在x轴的非负半轴上，终边经过点P(3,4)，则sin＝(　　)A．－  B．－C.   D.【答案】C　【解析】∵角α的终边经过点P(3,4)，∴sin α＝，cos α＝.∴sin＝sinα－＋＝sinα＋＝cos α＝.故选C.13．若角α的终边与角的终边关于直线y＝x对称，且α∈(－4π，4π)，则α＝________________________.【答案】－，－，，【解析】如图所示，设角的终边为OA，OA关于直线y＝x对称的射线为OB，则以OB为终边且在0～2π范围内的角为，故以OB为终边的角的集合为α.∵α∈(－4π，4π)，∴－4π<2kπ＋<4π，∴－<k<.∵k∈Z，∴k＝－2，－1,0,1.∴α＝－，－，，.14．若角θ的终边过点P(－4a,3a)(a≠0)，则sin θ＋cos θ等于________．【答案】±【解析】∵角θ的终边过点P(－4a,3a)(a≠0)，∴x＝－4a，y＝3a，r＝5|a|.当a>0时，r＝5a，sin θ＋cos θ＝＋＝－.当a<0时，r＝－5a，sin θ＋cos θ＝＋＝.故sin θ＋cos θ＝±.15.函数y＝lg(3－4sin2x)的定义域为________．【答案】　(k∈Z)【解析】　 ∵3－4sin2x>0，∴sin2x<，∴－<sin x<.利用三角函数线画出x满足条件的终边范围(如图阴影部分所示)，∴x∈(k∈Z)．16．已知角α的终边经过点(3a－9，a＋2)，且cos α≤0，sin α>0，则实数a的取值范围是________．【答案】(－2,3]【解析】∵cos α≤0，sin α>0，∴角α的终边落在第二象限或y轴的正半轴上．∴∴－2<a≤3.17．(2019·齐齐哈尔八中月考)已知角α的顶点在坐标原点，始边为x轴的非负半轴，终边上有一点P(3a,4a)，其中a≠0，求sin α，cos α，tan α.【解析】设r＝|OP|＝＝5|a|.当a>0时，r＝5a，∴sin α＝＝，cos α＝＝，tan α＝＝；当a<0时，r＝－5a，∴sin α＝－，cos α＝－，tan α＝.综上可知，sin α＝，cos α＝，tan α＝或sin α＝－，cos α＝－，tan α＝.18.如图，在平面直角坐标系xOy中，角α的始边与x轴的非负半轴重合且与单位圆相交于A点，它的终边与单位圆相交于x轴上方一点B，始边不动，终边在运动．(1)若点B的横坐标为－，求tan α的值；(2)若△AOB为等边三角形，写出与角α终边相同的角β的集合；(3)若α∈，请写出弓形AB的面积S与α的函数关系式．【解析】(1)由题意可得B，根据三角函数的定义得tan α＝＝－.(2)若△AOB为等边三角形，则B，可得tan∠AOB＝＝，故∠AOB＝；故与角α终边相同的角β的集合为β|β＝＋2kπ，k∈Z.(3)若α∈，则S扇形OAB＝αr2＝α，而S△AOB＝×1×1×sin α＝sin α，故弓形AB的面积S＝S扇形OAB－S△AOB＝α－sin α，α∈.