初中数学人教版七年级上册1.4.2 有理数的除法教案设计

这是一份初中数学人教版七年级上册1.4.2 有理数的除法教案设计，共2页。教案主要包含了温故提新，讲授新课，巩固知识，小结，布置作业等内容，欢迎下载使用。
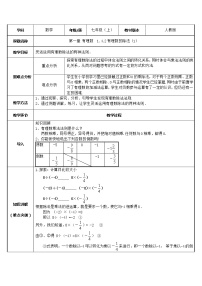
教学目标：


1、理解有理数除法的意义，熟练掌握有理数除法法则，会进行有理数的除法运算；


2、了解倒数概念，会求给定有理数的倒数；


3、通过将除法运算转化为乘法运算，培养学生的转化的思想；通过有理数的除法运算，培养学生的运算能力。


重点：除法法则和除法运算


重点：根据除法是乘法的逆运算，归纳出除法法则及商的符号的确定


教学过程：


一、温故提新：


1、小学里学过有关倒数的概念是什么？怎么求一个数的倒数？（用1除以这个数） 4和+ EQ \F(2,3) 的倒数是多少？0有倒数吗？为什么没有？


2、小学里学过的除法与乘法有何关系？例如10÷0.5=10×2；0÷5=0×（ EQ \F(1,5) ），你能总结总结出一句话吗？


归纳：除以一个数等于乘以这个数的倒数


3、5÷0=？，0÷0=？呢？（这些式子无意义）也就是说0是没有倒数的。


4、我们已知的求倒数的法则在有理数范围中同样适用吗？你能说说以下各数的倒数是多少吗？


4，2．5，－9，－37，－1，a, a－1, 3a, abc, －xy（各字母式不为0）


说明：一个数的倒数与其是正数或负数无关。


二、讲授新课


1、讲述：我们知道除法是乘法的逆运算，这套法则运用到有理数的范围内同样适用。例如，8÷4=8×( EQ \F(1,4) )=2；8÷(－4)=8×(－ EQ \F(1,4) )。那么，你知道（－8）÷（－4）=？，（－7）÷（－3.5）呢？


如果用字母表示，怎么表示？a÷b=a×( EQ \F(1,b) ) (b不为0).


2、由（－4）×（－1÷4）=1，4×( EQ \F(1,4) )=1等等式子，可知：互为倒数的两个数的积为1。


用字母表示为：a×（ EQ \F(1,a) ）=1 （a≠0）


3、通过上面的练习两个有理数相除，商的符号有什么规律？商的绝对值呢？通过练习我们可得出什么结论？


即有：两数相除，同号得正，异号得负，并把绝对值相除。0除以任何一个不为0的数仍得0。注意：零不能作除数


思考：下列等式成立吗？


（－8）÷（－4）=（－8）×（－ EQ \F(1,4) ）；由此你得出什么规律？


一般的，有理数乘法与除法之间有以下关系：


除以一个数（不等于零），等于乘以这个数的倒数


三、巩固知识


例5


教师：分数可以理解为分子除以分母。


例6


四、小结：（1）有理数的除法法则是什么？（2）如何运用除法法则进行有理数的除法运算？


五、布置作业