初中数学第十一章 三角形综合与测试单元测试课后复习题

这是一份初中数学第十一章 三角形综合与测试单元测试课后复习题，共7页。试卷主要包含了给出下列说法，在同一平面内，等内容，欢迎下载使用。
一．选择题（共10小题，满分30分，每小题3分）


1．给出下列说法：①三条线段组成的图形叫三角形；②三角形的角平分线是射线；③三角形的高所在的直线交于一点，这一


点不在三角形内就在三角形外；④任何一个三角形都有三条高、三条中线、三条角平分线；⑤三角形的三条角平分线交于一点，且这点在三角形内．正确的说法有（ ）


A．1个B．2个C．3个D．4个


2．已知一个三角形两边的长分别是2和5，那么第三边的边长可能是下列各数中的（ ）


A．1B．2C．3D．5


3．如图，将一副三角板按如图方式叠放，则角α等于（ ）





A．165°B．135°C．105°D．75°


4．如图所示，l1∥l2，则下列式子中值为180°的是（ ）





A．α+β+γB．α+β﹣γC．β+γ﹣αD．α﹣β+γ


5．在同一平面内，（ ）


A．不重合的两条直线要么平行要么相交


B．直角三角形的两锐角互补


C．两条直线平行，同旁内角相等


D．垂直于同一条直线的两直线互相垂直


6．下面设计的原理不是利用三角形稳定性的是（ ）


A．三角形的房架


B．由四边形组成的伸缩门


C．斜钉一根木条的长方形窗框


D．自行车的三角形车架


7．一个n边形的内角和为540°，则n的值为（ ）


A．4B．5C．6D．7


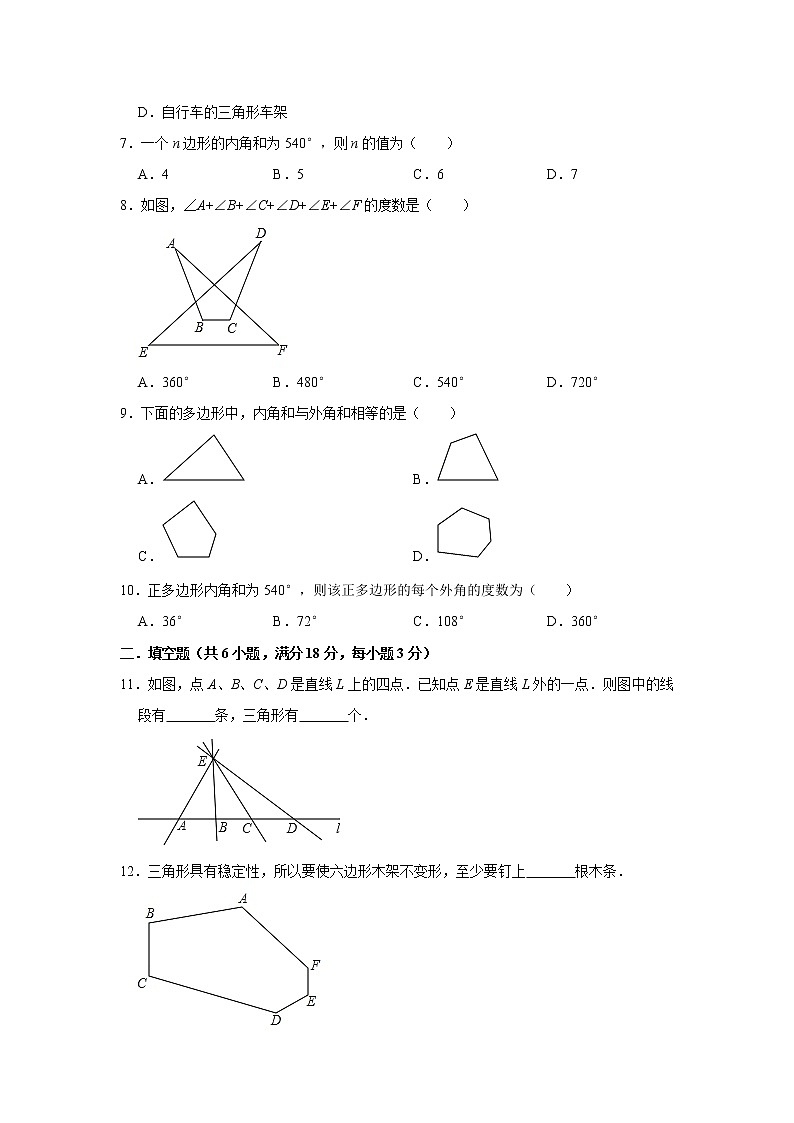
8．如图，∠A+∠B+∠C+∠D+∠E+∠F的度数是（ ）





A．360°B．480°C．540°D．720°


9．下面的多边形中，内角和与外角和相等的是（ ）


A．B．


C．D．


10．正多边形内角和为540°，则该正多边形的每个外角的度数为（ ）


A．36°B．72°C．108°D．360°


二．填空题（共6小题，满分18分，每小题3分）


11．如图，点A、B、C、D是直线L上的四点．已知点E是直线L外的一点．则图中的线段有 条，三角形有 个．





12．三角形具有稳定性，所以要使六边形木架不变形，至少要钉上 根木条．





13．木工师傅有两根长分别是10cm，30cm的木条，他要找第三根木条，将它们钉成一个三角形框架，现有20cm、35cm、50cm的四根木条，他可以选择 长的木条．


14．我们给出如下定义：若一个四边形的两条对角线相等，则称这个四边形为等对角线四边形．写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称 ．


15．一个n边形的内角和是它外角和的6倍，则n＝ ．


16．已知一个多边形的内角和与外角和之比是3：2，则这个多边形的边数为 ．


三．解答题（共7小题，满分72分）


17．（8分）已知△ABC中，AB＝6，BC＝4，求AC的取值范围．


18．（8分）如图，已知∠ABC的平分线BD和∠ACE的平分线CD相交于D，∠DBC＝∠D


（1）AB与CD平行吗？请说明理由；


（2）如果∠A＝54°，求∠D的度数．





19．（10分）如图，△ABC中，CE是△ABC的外角∠ACD的角平分线，∠ACE＝70°，∠B＝55°．求∠A的度数．





20．（10分）如图，∠C＝90°，∠1＝∠2，△ADE是直角三角形吗？为什么？





21．（12分）一个多边形的内角和是它的外角和的5倍，求这个多边形的边数．


22．（12分）如图，四边形ABCD中，∠ADB＝60°，∠CDB＝50°．


（1）若AD∥BC，AB∥CD，求∠ABC的度数；


（2）若∠A＝70°，请写出图中平行的线段，并说明理由．





23．（12分）一个多边形内角和的度数比外角和的度数的4倍多180度，求多边形的边数．





参考答案


一．选择题


1．B．


2． D．


3． A．


4． B．


5． A．


6． B．


7． B．


8． A．


9． B．


10． B．


二．填空题


11． 10；6．


12． 3．


13． 35cm．


14．矩形、正方形．答案不唯一．


15． 14．


16． 5．


三．解答题


17．解：根据三角形的三边关系，得


6﹣4＜AC＜6+4，


∴2＜AC＜10．


AC的取值范围是：2＜AC＜10．


18．解：（1）AB与CD平行，理由如下：


∵BD平分∠ABC，


∴∠ABD＝∠DBC，


∵∠DBC＝∠D，


∴∠ABD＝∠D，


∴AB∥CD；


（2）由三角形的外角性质得，∠ACE＝∠A+∠ABC，


∠DCE＝∠D+∠DBC，


∵BD平分∠ABC，CD平分∠ACE，


∴∠ABC＝2∠DBC，∠ACE＝2∠DCE，


∴∠A+∠ABC＝2（∠D+∠DBC），


整理得，∠A＝2∠D，


∵∠A＝54°，


∴∠D＝×54°＝27°．





19．解：∵CE是∠ACD的角平分线，


∴∠ACD＝2∠ACE，


∵∠ACE＝70°，


∴∠ACD＝140°，


∵∠ACD是△ABC的外角，


∴∠ACD＝∠A+∠B，


∵∠B＝55°，


∴∠A＝∠ACD﹣∠B＝140°﹣55°＝85°．


20．解：∵∠C＝90°，


∴∠A+∠2＝90°，


∵∠1＝∠2，


∴∠A+∠1＝90°，


∴∠ADE＝90°，


∴△ADE是直角三角形．


21．解：设多边形的边数为n，


由题意得，（n﹣2）•180°＝5×360°，


解得n＝12，


所以，这个多边形是十二边形．


22．解：（1）∵∠ADB＝60°，∠CDB＝50°，


∴∠ADC＝110°


∵AD∥BC，


∴∠A＝70°，


∵AB∥CD，


∴∠ABC＝110°；


（2）AB∥CD．理由如下：


∵∠ADB＝60°，∠A＝70°，


∴∠ABD＝50°，


∴∠CDB＝∠ABD＝50°，


∴AB∥CD．


23．解：设多边形的边数为n．


∵多边形的外角和是360°，内角和的度数比外角和的度数的4倍多180度，


∴可得方程（n﹣2）180°＝4×360°+180°


解得n＝11．


多边形的边数为11．