

备考2019年高考物理一轮复习文档:第9章 第2讲《磁场对运动电荷的作用》练习(含解析)
展开板块三限时规范特训
时间:45分钟 满分:100分
一、选择题(本题共10小题,每小题6分,共60分。其中1~5为单选,6~10为多选)
1. [2017·甘肃省一模]如图所示,两相邻且范围足够大的匀强磁场区域Ⅰ和Ⅱ的磁感应强度方向平行,大小分别为B和2B。一带正电粒子(不计重力)以速度v从磁场分界线MN上某处射入磁场区域Ⅰ,其速度方向与磁场方向垂直且与分界线MN成60°角,经过t1时间后粒子进入到磁场区域Ⅱ,又经过t2时间后回到区域Ⅰ,设粒子在区域Ⅰ、Ⅱ中的角速度分别为ω1、ω2,则( )
A.ω1∶ω2=1∶1 B.ω1∶ω2=2∶1
C.t1∶t2=1∶1 D.t1∶t2=2∶1
答案 C
解析 由qvB=m和v=ωR得ω=,故ω1∶ω2=1∶2;粒子在Ⅰ中的轨迹对应的圆心角均为120°,在Ⅱ中的轨迹对应的圆心角为240°由T=T2=和t=·T知t1∶t2=1∶1。
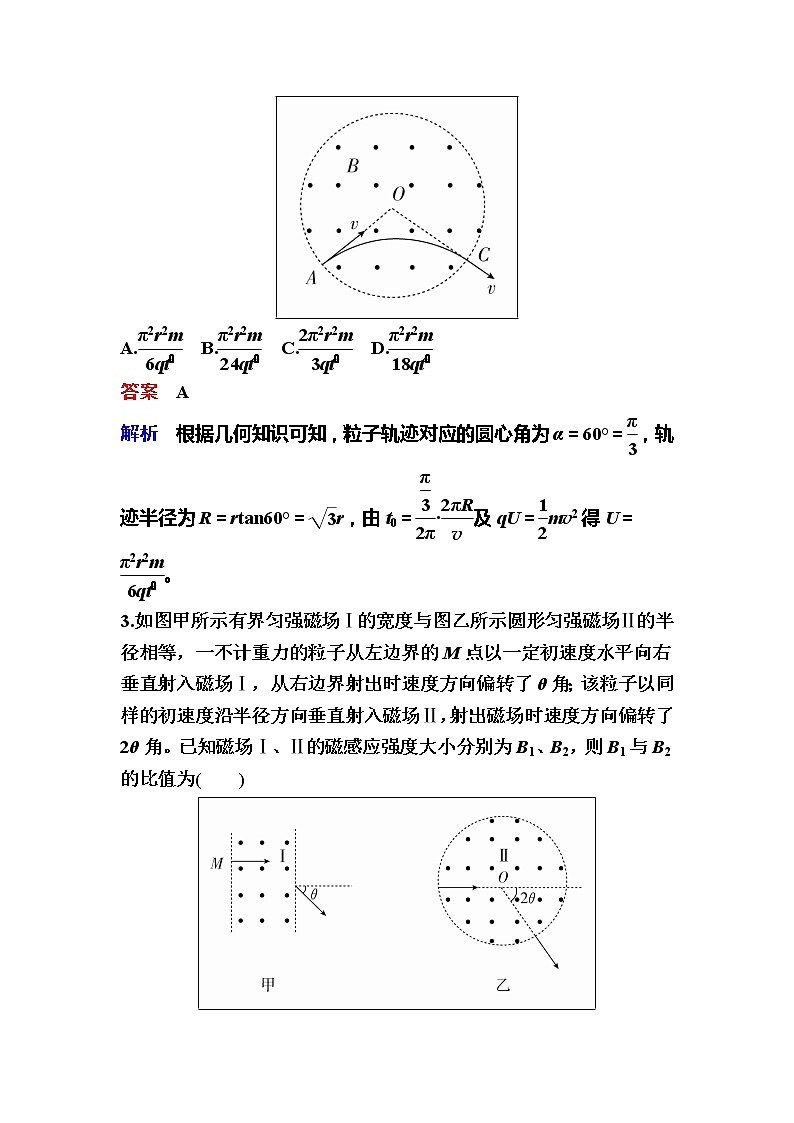
2. [2017·四川四市二诊]如图所示,半径为r的圆形空间内,存在垂直于纸面向外的匀强磁场,一个质量为m,电荷量为q的带电粒子(不计重力),从静止经电场加速后从圆形空间边缘上的A点沿半径方向垂直于磁场方向射入磁场,在C点射出,已知∠AOC=120°,粒子在磁场中运动时间为t0,则加速电场的电压是( )
A. B. C. D.
答案 A
解析 根据几何知识可知,粒子轨迹对应的圆心角为α=60°=,轨迹半径为R=rtan60°=r,由t0=·及qU=mv2得U=。
3.如图甲所示有界匀强磁场Ⅰ的宽度与图乙所示圆形匀强磁场Ⅱ的半径相等,一不计重力的粒子从左边界的M点以一定初速度水平向右垂直射入磁场Ⅰ,从右边界射出时速度方向偏转了θ角;该粒子以同样的初速度沿半径方向垂直射入磁场Ⅱ,射出磁场时速度方向偏转了2θ角。已知磁场Ⅰ、Ⅱ的磁感应强度大小分别为B1、B2,则B1与B2的比值为( )
A.2cosθ B.sinθ C.cosθ D.tanθ
答案 C
解析 设有界磁场Ⅰ宽度为d,则粒子在磁场Ⅰ和磁场Ⅱ中的运动轨迹分别如图所示,由洛伦兹力提供向心力知Bqv=m,得B=,由几何关系知d=r1sinθ,d=r2tanθ,联立得=cosθ,C正确。
4. [2016·安徽芜湖模拟]如图所示,在x轴上方存在垂直于纸面向里的匀强磁场,磁感应强度为B。在xOy平面内,从原点O处沿与x轴正方向成θ角(0<θ<π)以速率v发射一个带正电的粒子(重力不计)。则下列说法正确的是( )
A.若v一定,θ越大,则粒子在磁场中运动的时间越短
B.若v一定,θ越大,则粒子在离开磁场的位置距O点越远
C.若θ一定,v越大,则粒子在磁场中运动的角速度越大
D.若θ一定,v越大,则粒子在磁场中运动的时间越短
答案 A
解析 由左手定则可知,带正电的粒子向左偏转。轨迹对应的圆心角α=2π-2θ,粒子在磁场中运动时间t=T=。若v一定,θ越大,则粒子在磁场中运动的时间越短,A项正确;若v一定,θ等于90°时,粒子在离开磁场的位置距O点最远,B项错误;若θ一定,粒子在磁场中运动的周期与v无关,粒子在磁场中运动的角速度与v无关,粒子在磁场中运动的时间与v无关,C、D两项错误。
5.如图甲所示为足够大空间内存在水平方向的匀强磁场,在磁场中A、B两物块叠在一起置于光滑水平面上,物块A带正电,物块B不带电且表面绝缘,A、B接触面粗糙,自t=0时刻起用水平恒力F作用在物块B上,两物块由静止开始做匀加速直线运动。乙图图象的横轴表示时间,则纵轴y可以表示( )
A.A所受摩擦力的大小 B.B对地面压力的大小
C.A所受合力的大小 D.B所受摩擦力的大小
答案 B
解析 由于A、B由静止开始做匀加速直线运动,所以合外力恒定,且B所受摩擦力大小等于B对A的摩擦力,以A为研究对象,由牛顿第二定律得f=mAa,不随时间改变,故A、C、D选项错误。A带正电,所受洛伦兹力向下,A受支持力FNA=mAg+Bqv=mAg+Bqat,符合图象。B受地面支持力FNB=(mA+mB)g+Bqv=(mA+mB)g+Bqat,也符合图象,故B选项正确。
6. [2017·广西南宁一模]如图所示,MN是纸面内的一条直线,其所在空间充满与纸面平行的匀强电场或与纸面垂直的匀强磁场(区域都足够大),现有一重力不计的带电粒子从MN上的O点以平行于纸面的初速度v0射入,下列有关判断正确的是( )
A.如果粒子回到MN上时速度增大,则空间存在的一定是电场
B.如果粒子回到MN上时速度大小不变,则该空间存在的一定是电场
C.若只改变粒子的速度大小,发现粒子再回到MN上时与其所成夹角不变,则该空间存在的一定是磁场
D.若只改变粒子的速度大小,发现粒子再回到MN所用的时间不变,则该空间存在的一定是磁场
答案 AD
解析 洛伦兹力对带电粒子不做功,不能使粒子速度增大,静电力可对带电粒子做功,动能增大,故A正确;若存在匀强磁场,则粒子返回MN时速率不变,故B错误;若MN为一等势面,则粒子回到MN时,速度大小不变,且沿MN方向的速度不变,则速度与MN夹角不变,故C错误;由T=知,粒子在磁场中运动的时间与速率无关,故D正确。
7. [2017·甘肃省模拟]如图所示,在一等腰三角形ACD区域内有垂直纸面向外的匀强磁场,磁场的磁感应强度大小为B。一质量为m、电荷量为q的带正电粒子(不计重力)从AC边的中点O垂直于AC边射入该匀强磁场区域,若该三角形的两直角边长均为2l,则下列关于粒子运动的说法中正确的是( )
A.若该粒子的入射速度为v=,则粒子一定从CD边射出磁场,且距点C的距离为l
B.若要使粒子从CD边射出,则该粒子从O点入射的最大速度应为v=
C.若要使粒子从AC边射出,则该粒子从O点入射的最大速度应为v=
D.该粒子以不同的速度入射时,在磁场中运动的最长时间为
答案 ACD
解析 若该粒子的入射速度为v=,由Bqv=m解得r=l,根据几何关系可知,粒子一定从CD边距C点为l的位置离开磁场,故A正确;v=,速度越大,半径越大,根据几何关系可知,若要使粒子从CD边射出,则粒子速度最大时,轨迹与AD边相切,则由几何关系可知,最大半径一定大于l,故B错误;若要使粒子从AC边射出,则该粒子从O点入射的最大半径为,因此最大速度应为v=,故C正确;粒子在磁场中做匀速圆周运动的周期为,根据几何关系可知,粒子在磁场中运动的最大圆心角为180°,故最长时间为,故D正确。
8. 如图所示,宽d=4 cm的有界匀强磁场,纵向范围足够大,磁场方向垂直纸面向里。现有一群正粒子从O点以相同的速率沿纸面不同方向进入磁场,若粒子在磁场中做匀速圆周运动的轨道半径为r=10 cm,则( )
A.右边界:-8 cm<y<8 cm有粒子射出
B.右边界:0<y<8 cm有粒子射出
C.左边界:y>8 cm有粒子射出
D.左边界:0<y<16 cm有粒子射出
答案 AD
解析 根据左手定则,正粒子在匀强磁场中将沿逆时针方向转动,由轨道半径r=10 cm画出粒子的两种临界运动轨迹,如图所示,则OO1=O1A=OO2=O2C=O2E=10 cm,由几何知识求得AB=BC=8 cm,OE=16 cm,因此答案为A、D。
9. 如图所示,MN是磁感应强度为B的匀强磁场的边界。一质量为m、电荷量为q的粒子在纸面内从O点射入磁场。若粒子速度为v0,最远可落在边界上的A点。下列说法中正确的有( )
A.若粒子落在A点的左侧,其速度一定小于v0
B.若粒子落在A点的右侧,其速度一定大于v0
C.若粒子落在A点左右两侧d的范围内,其速度不可能小于v0-
D.若粒子落在A点左右两侧d的范围内,其速度不可能大于v0+
答案 BC
解析 因粒子由O点以速度v0入射时,最远落在A点,又粒子在O点垂直射入磁场时,在边界上的落点最远,即=,所以粒子若落在A的右侧,速度应大于v0,B正确;当粒子落在A的左侧时,由于不一定是垂直入射,所以速度可能等于、大于或小于v0,A错误;当粒子射到A点左侧相距d的点时,最小速度为vmin,则=,又因=,所以vmin=v0-,所以粒子落在A点左右两侧d的范围内,其速度不可能小于vmin=v0-,C正确;当粒子射到A点右侧相距d的点时,最小速度为v1,则=,又因=,即v1=v0+,D错误。
10. [2016·河北、河南、山西质监]如图所示,在xOy平面内的y轴和虚线之间除圆形区域外的空间存在匀强磁场,磁场方向垂直纸面向外,磁感应强度大小为B。虚线经过Q点(3L,0)且与y轴平行。圆形区域的圆心P的坐标为(2L,0),半径为L。一个质量为m,电荷量为q的带正电的粒子从y轴上某点垂直y轴进入磁场,不计粒子的重力,则( )
A.如果粒子没有经过圆形区域到达了Q点,则粒子的入射速度为v=
B.如果粒子没有经过圆形区域到达了Q点,则粒子的入射速度为v=
C.粒子第一次从P点经过了x轴,则粒子的最小入射速度为vmin=
D.粒子第一次从P点经过了x轴,则粒子的最小入射速度为vmin=
答案 AC
解析 若粒子没经过圆形区域到达了Q点,则轨迹如图甲,和圆形区域相切于Q点,则r=3L,根据牛顿第二定律Bqv=得v=,A选项正确,B选项错误。粒子第一次从P点经过了x轴,如图乙所示。
设在磁场中转过的圆心角为θ,由几何关系得
rsinθ+Lcosθ=2L,得r=L=L=L
=L=L≥L。据Bqv=得vmin=,选项C正确,选项D错误。
二、非选择题(本题共2小题,共40分)
11. [2017·河北衡水一模](20分)如图所示,在等边三角形ABC内存在着垂直纸面向里的匀强磁场,磁感应强度大小为B0。在等边三角形ABC外存在着垂直于纸面向外的匀强磁场,磁感应强度大小为2B0。等边三角形ABC边长为a,在顶点A处放置一“”形的挡板P,挡板夹角为60°,挡板两边正好分别与AB、AC重合,挡板左右两侧板长均为。在顶点B处沿∠ABC的角平分线方向,有大量不同速率的带电粒子射出,这些粒子的电荷量均为+q,质量均为m,其速率满足<v<,已知带电粒子打在挡板上后立即被吸收,所有能够到达AC边的粒子中,打在D点的粒子速率最小,若不计粒子间的相互作用力,求AD之间的距离。
答案 a
解析 发射粒子速率满足<v<
洛伦兹力提供向心力F洛=qvB0
F洛=m
得r=
可知在三角形ABC内部,带电粒子的轨道半径满足<r1<a
带电粒子在三角形ABC外部半径r2=
由几何关系可知,能够打在AC边上的速率最小值
所对应半径(在三角形外部)为
此时可证明该速率所对圆心O恰好在AC边上,且
AO=
如图所示,由几何关系可知AD=a
12. [2016·海南高考](20分)如图,A、C两点分别位于x轴和y轴上,∠OCA=30°,OA的长度为L。在△OCA区域内有垂直于xOy平面向里的匀强磁场,质量为m、电荷量为q的带正电粒子,以平行于y轴的方向从OA边射入磁场。已知粒子从某点入射时,恰好垂直于OC边射出磁场,且粒子在磁场中运动的时间为t0。不计重力。
(1)求磁场的磁感应强度的大小;
(2)若粒子先后从两不同点以相同的速度射入磁场,恰好从OC边上的同一点射出磁场,求该粒子这两次在磁场中运动的时间之和;
(3)若粒子从某点射入磁场后,其运动轨迹与AC边相切,且在磁场内运动的时间为t0,求粒子此次入射速度的大小。
答案 (1) (2)2t0 (3)
解析 (1)粒子在磁场中做匀速圆周运动,在时间t0内其速度方向改变了90°,故其周期
T=4t0①
设磁感应强度大小为B,粒子速度大小为v,圆周运动的半径为r。由洛伦兹力公式和牛顿第二定律得
qvB=m②
匀速圆周运动的速度满足
v=③
联立①②③式得
B=④
(2)设粒子从OA边两个不同位置射入磁场,能从OC边上的同一点P射出磁场,粒子在磁场中运动的轨迹如图甲所示。设两轨迹所对应的圆心角分别为θ1和θ2。由几何关系知
θ1=180°-θ2⑤
粒子两次在磁场中运动的时间分别为t1与t2,则
t1+t2==2t0⑥
(3)如图乙,由题给条件可知,该粒子在磁场区域中的轨迹圆弧对应的圆心角为150°。设O′为圆弧的圆心,圆弧的半径为r0,圆弧与AC相切于B点,从D点射出磁场,由几何关系和题给条件可知,此时有
∠OO′D=∠BO′A=30°⑦
r0cos∠OO′D+=L⑧
设粒子此次入射速度的大小为v0,由圆周运动规律得
v0=⑨
联立①⑦⑧⑨式得v0=⑩








