初中数学北师大版八年级上册3 勾股定理的应用优秀课件ppt

这是一份初中数学北师大版八年级上册3 勾股定理的应用优秀课件ppt，共33页。PPT课件主要包含了学习目标，情景引入，蚂蚁A→B的路线，数学思想，立体图形，平面图形，牛奶盒，△ABC为直角三角形，解得x5，实际问题等内容，欢迎下载使用。

1.学会运用勾股定理求立体图形中两点之间的最短距离．（重点）2.能够运用勾股定理解决实际生活中的问题.(重点,难点)
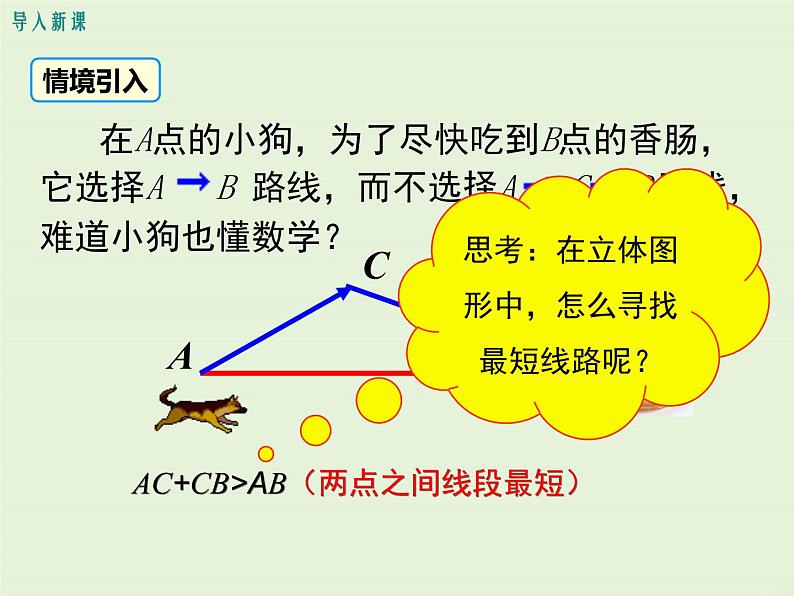
在A点的小狗，为了尽快吃到B点的香肠，它选择A B 路线，而不选择A C B路线，难道小狗也懂数学？
AC+CB>AB（两点之间线段最短）
思考：在立体图形中，怎么寻找最短线路呢？
数学来源于生活，勾股定理的应用在生活中无处不在，观看下面视频，你们能理解曾小贤和胡一菲的做法吗？
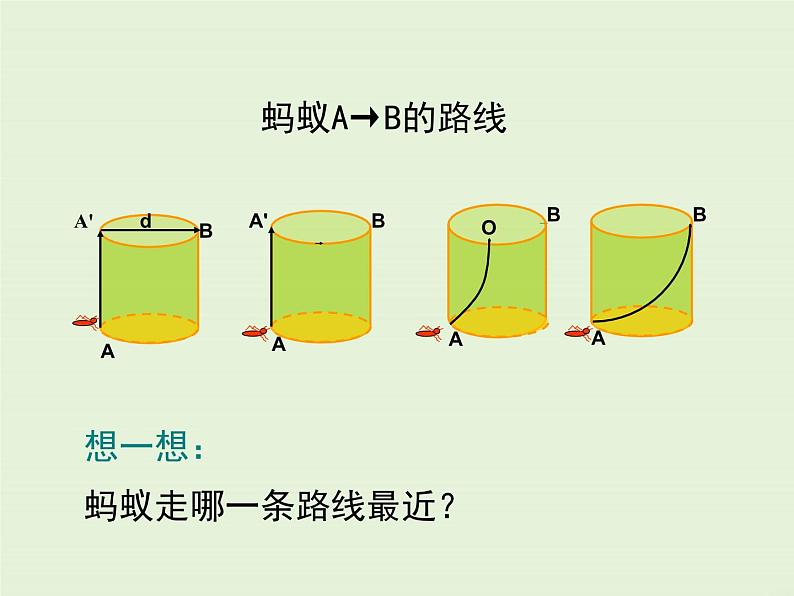
问题：在一个圆柱石凳上，若小明在吃东西时留下了一点食物在B处，恰好一只在A处的蚂蚁捕捉到这一信息，于是它想从A处爬向B处，你们想一想，蚂蚁怎么走最近？
想一想：蚂蚁走哪一条路线最近？
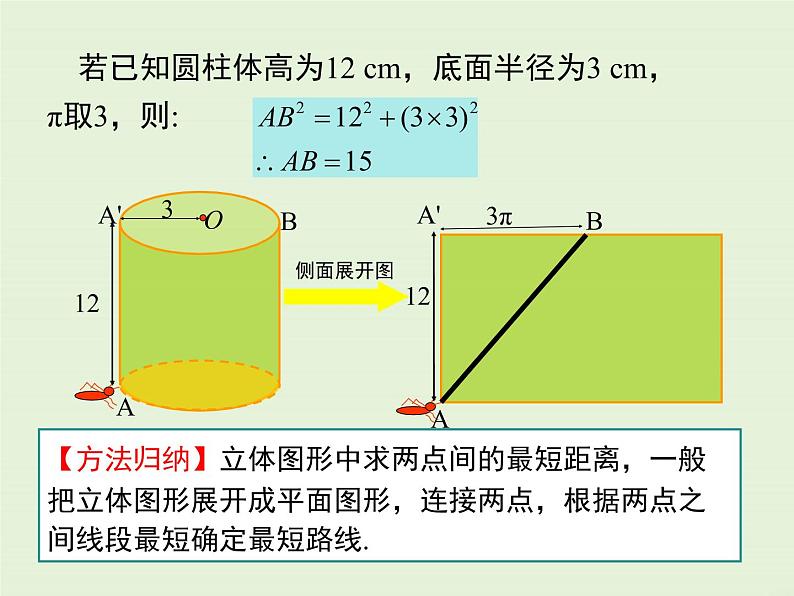
若已知圆柱体高为12 cm，底面半径为3 cm，π取3，则:
【方法归纳】立体图形中求两点间的最短距离，一般把立体图形展开成平面图形，连接两点，根据两点之间线段最短确定最短路线.
例1 有一个圆柱形油罐，要以A点环绕油罐建梯子，正好建在A点的正上方点B处，问梯子最短需多少米?(已知油罐的底面半径是2 m，高AB是5 m，π取3）
解：油罐的展开图如图，则AB'为梯子的最短距离. ∵AA'=2×3×2=12, A'B'=5,∴AB'=13. 即梯子最短需13米.
变式1：当小蚂蚁爬到距离上底3cm的点E时，小明同学拿饮料瓶的手一抖，那滴甜甜的饮料就顺着瓶子外壁滑到了距离下底3cm的点F处，小蚂蚁到达点F处的最短路程是多少？（π取3）
解：如图，可知△ECF为直角三角形，由勾股定理,得 EF2=EC2+CF2=82+(12-3-3)2=100，∴EF=10(cm).
变式2：看到小蚂蚁终于喝到饮料的兴奋劲儿，小明又灵光乍现，拿出了牛奶盒，把小蚂蚁放在了点A处，并在点B处放上了点儿火腿肠粒，你能帮小蚂蚁找到完成任务的最短路程么？
AB12 =102 +（6+8）2 =296
AB22= 82 +（10+6）2 =320
AB32= 62 +（10+8）2 =360
问题：李叔叔想要检测雕塑底座正面的AD边和BC边是否分别垂直于底边AB，但他随身只带了卷尺.（1）你能替他想办法完成任务吗？
解:连接对角线AC，只要分别量出AB、BC、AC的长度即可.
AB2+BC2=AC2
（2）量得AD长是30 cm，AB长是40 cm，BD长是50 cm. AD边垂直于AB边吗？
解:AD2+AB2=302+402=502=BD2，
得∠DAB=90°，AD边垂直于AB边.
（3）若随身只有一个长度为20 cm的刻度尺，能有办法检验AD边是否垂直于AB边吗？
解:在AD上取点M,使AM=9,在AB上取点N使AN=12,测量MN是否是15，是，就是垂直；不是，就是不垂直.
例2 如图是一个滑梯示意图，若将滑道AC水平放置，则刚好与AB一样长.已知滑梯的高度CE=3m，CD=1m，试求滑道AC的长.
故滑道AC的长度为5 m.
解：设滑道AC的长度为x m，则AB的长也为x m，AE的长度为（x-1）m.
在Rt△ACE中，∠AEC=90°，
由勾股定理得AE2+CE2=AC2，
即（x-1）2+32=x2，
例3 一个门框的尺寸如图所示，一块长3m,宽2.2m的长方形薄木板能否从门框内通过?为什么?
解：在Rt△ABC中，根据勾股定理，
AC2=AB2+BC2=12+22=5
因为AC大于木板的宽2.2m,所以木板能从门框内通过.
分析：可以看出木板横着，竖着都不能通过，只能斜着.门框AC的长度是斜着能通过的最大长度，只要AC的长大于木板的宽就能通过.
解：在Rt△ABC中，根据勾股定理得
OB2=AB2-OA2=2.62-2.42=1，
在Rt△COD中，根据勾股定理得
OD2=CD2-OC2=2.62-(2.4-0.5)2=3.15,
∴梯子的顶端沿墙下滑0.5m时，梯子底端并不是也外移0.5m，而是外移约0.77m.
例4 如图，一架2.6m长的梯子AB斜靠在一竖直的墙AO上，这时AO为2.4m. 如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
例5 在一次台风的袭击中，小明家房前的一棵大树在离地面6米处断裂，树的顶部落在离树根底部8米处.你能告诉小明这棵树折断之前有多高吗？
解：根据题意可以构建一直角三角形模型，如图.在Rt△ABC中，AC=6米，BC=8米，由勾股定理得
∴这棵树在折断之前的高度是10+6=16（米）.
利用勾股定理解决实际问题的一般步骤：
（1）读懂题意，分析已知、未知间的关系；
（2）构造直角三角形；
（3）利用勾股定理等列方程；
例6 如图，在一次夏令营中，小明从营地A出发，沿北偏东53°方向走了400m到达点B，然后再沿北偏西37°方向走了300m到达目的地C.求A、C两点之间的距离．
解：如图，过点B作BE∥AD.∴∠DAB＝∠ABE＝53°.∵37°＋∠CBA＋∠ABE＝180°，∴∠CBA＝90°，∴AC2＝BC2＋AB2＝3002＋4002＝5002，∴AC＝500m，即A、C两点间的距离为500m.
此类问题解题的关键是将实际问题转化为数学问题；在数学模型(直角三角形)中，应用勾股定理或勾股定理的逆定理解题．
1．如图是一张直角三角形的纸片，两直角边AC＝6 cm，BC＝8 cm，将△ABC折叠，使点B与点A重合，折痕为DE，则BE的长为（ ） A.4 cm B.5 cm C.6 cm D.10 cm
2．有一个高为1.5 m，半径是1 m的圆柱形油桶，在靠近边的地方有一小孔，从孔中插入一铁棒，已知铁棒在油桶外的部分为0.5 m，问这根铁棒有多长？
解:设伸入油桶中的长度为x m,则最长时:
所以最长是2.5+0.5=3(m).
答:这根铁棒的长应在2～3 m之间.
所以最短是1.5+0.5=2(m).
梯子的顶端沿墙下滑4 m,梯子底端外移8 m.
解：在Rt△AOB中，
3.一个25m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为24m,如果梯子的顶端A沿墙下滑4m,那么梯子底端B也外移4m吗?
4.我国古代数学著作《九章算术》中记载了一道有趣的问题，这个问题的意思是：有一个水池，水面是一个边长为10尺的正方形，在水池的中央有一根新生的芦苇，它高出水面1尺，如果把这根芦苇垂直拉向岸边，它的顶端恰好到达岸边的水面，请问这个水池的深度和这根芦苇的长度各是多少？
解：设水池的水深AC为x尺，则这根芦苇长AD=AB=（x+1）尺，
在直角三角形ABC中，BC=5尺
由勾股定理得，BC2+AC2=AB2
即 52+ x2= (x+1)2
25+ x2= x2+2x+1，
∴ x=12， x+1=13.
答：水池的水深12尺，这根芦苇长13尺.
5. 为筹备迎接新生晚会，同学们设计了一个圆筒形灯罩，底色漆成白色，然后缠绕红色油纸，如图①.已知圆筒的高为108cm，其横截面周长为36cm，如果在表面均匀缠绕油纸4圈，应裁剪多长的油纸？
解：如图②，在Rt△ABC中，因为AC＝36cm，BC＝108÷4＝27(cm)．由勾股定理，得AB2＝AC2＋BC2＝362＋272＝2025＝452，所以AB＝45cm，所以整个油纸的长为45×4＝180(cm)．