初中数学华师大版七年级上册2 垂线优秀ppt课件

这是一份初中数学华师大版七年级上册2 垂线优秀ppt课件，共19页。PPT课件主要包含了学习目标，情境引入，交点O叫做垂足，总结归纳，m⊥n，典例精析，问题引导，符号语言，放2靠3画，无数条等内容，欢迎下载使用。

1.理解垂线的概念及画法；（重点） 2. 知道垂线段和点到直线的距离的概念，并会应用解决问题. （重点、难点）
日常生活中，如下图中的两条直线的关系很常见，你能再举出其他例子吗？
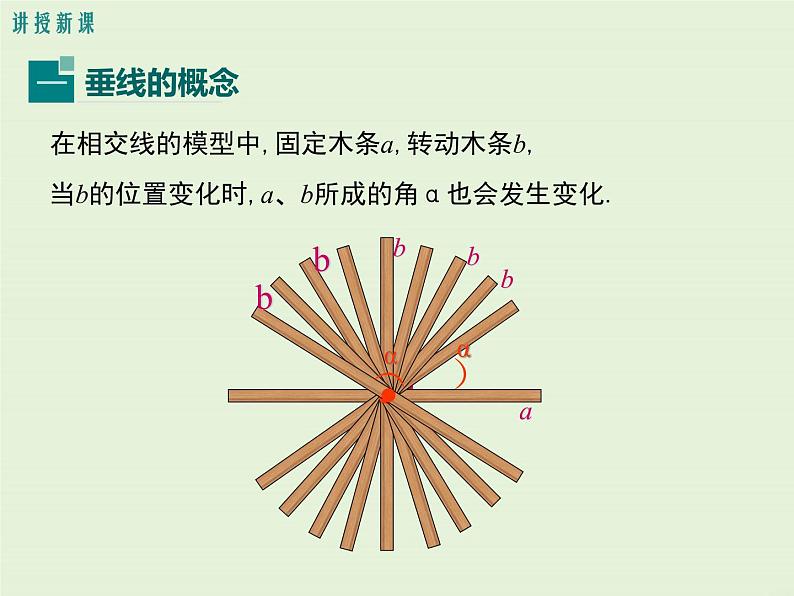
在相交线的模型中,固定木条a,转动木条b,
当b的位置变化时,a、b所成的角α也会发生变化.
问题 如图，当∠AOC＝90°时，∠BOD、∠AOD、∠BOC等于多少度？为什么？
由对顶角和邻补角的性质，知当∠AOC＝90°时，∠BOD=∠AOD=∠BOC=90°.
1.垂线的定义：当两条直线AB和CD所成的四个角中，如果有一个角是直角，其他三个角也都为直角，此时，这两条直线互相垂直.其中一条直线叫做另一条直线的垂线.
2.垂直用符号 “⊥”来表示，读作“垂直于”。如“直线AB垂直于直线CD”，就记作“AB⊥CD”.
4.垂直是相交的特殊情况.
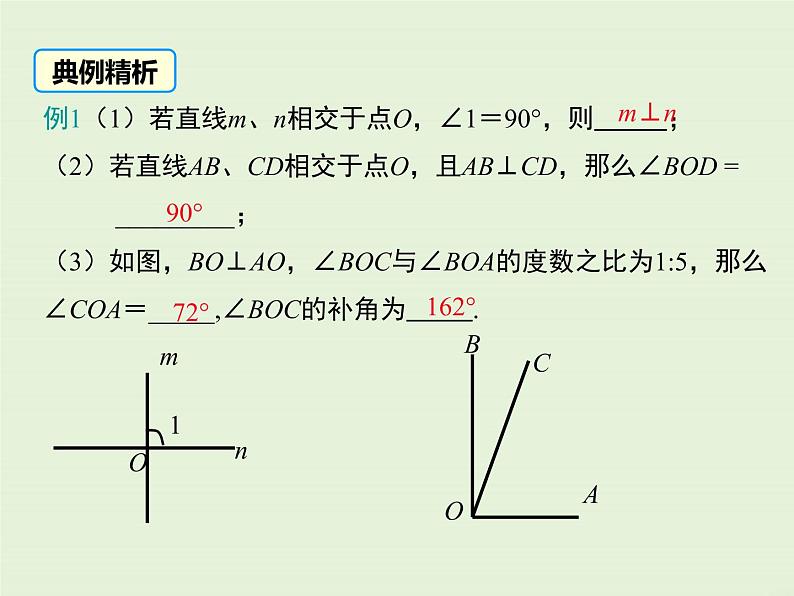
例1（1）若直线m、n相交于点O，∠1＝90°，则 ；（2）若直线AB、CD相交于点O，且AB⊥CD，那么∠BOD = _________；（3）如图，BO⊥AO，∠BOC与∠BOA的度数之比为1:5，那么∠COA＝_____,∠BOC的补角为 .
(1)画已知直线l的垂线能画几条?(2)过直线l上的一点A画l的垂线,这样的垂线能画几条?(3)过直线l外的一点B画l的垂线,这样的垂线能画几条?
如图，当直线AB与CD相交于O点，∠AOD=90°时，AB⊥CD，垂足为O.
①判定：∵∠AOD=90°（已知） ∴AB⊥CD（垂直的定义）
反之，若直线AB与CD垂直，垂足为O，那么，∠AOD=90°.
②性质：∵ AB⊥CD （已知） ∴ ∠AOD=90° （垂直的定义）
(∠AOC=∠BOC=∠BOD=90°)
问题：这样画l的垂线可以画几条？
如图，已知直线 l,作l的垂线.
1.放2.靠3.移4.画
如图，已知直线 l 和l上的一点A ,作l的垂线.
根据以上操作，你能得出什么结论
过一点有且只有一条直线与已知直线垂直.
（1）“过一点”中的点，可以在已知直线上，也可以在 已知直线外；（2）“有且只有”中，“有”指存在，“只有”指唯一性.
连接直线外一点与直线上各点的所有线段中垂线段最短.
线段AD的长度叫做点A到直线l的距离.
例2 在灌溉时，要把河中的水引到农田P处，如何挖掘能使渠道最短？请画出图来，并说明理由.
1.两条直线相交所成的四个角中，下列条件中能判定两条直线垂直的是( )A. 有两个角相等 B.有两对角相等C. 有三个角相等 D.有四对邻补角
2.如图, AC⊥BC, ∠C=90° ,线段AC、BC、CD中最短的是( )A. AC B. BC C. CD D. 不能确定
3.过点P 向线段AB 所在直线引垂线，正确的是（ ）
A B C D
5.如图，已知直线AB、CD都经过O点，OE为射线，若∠1＝35°,∠2＝55°，则OE与AB的位置关系是 .
4.下列说法正确的是（ ）A.线段AB叫做点B到直线AC的距离B.线段AB的长度叫做点A到直线AC的距离C.线段BD的长度叫做点D到直线BC的距离D.线段BD的长度叫做点B到直线AC的距离