


初中数学华师大版八年级上册5 边边边试讲课ppt课件
展开1.掌握三角形全等的“”判定,并能应用它判别两个 三角形是否全等,以及运用该条件解决一些简单的实 际问题.(重点) 2.由探索三角形全等条件的过程,体会由操作、归纳获 得数学结论的过程.(难点)
到目前为止,我们学习了哪几种判定三角形全等的方法?
1.根据定义;2.公理,;定理
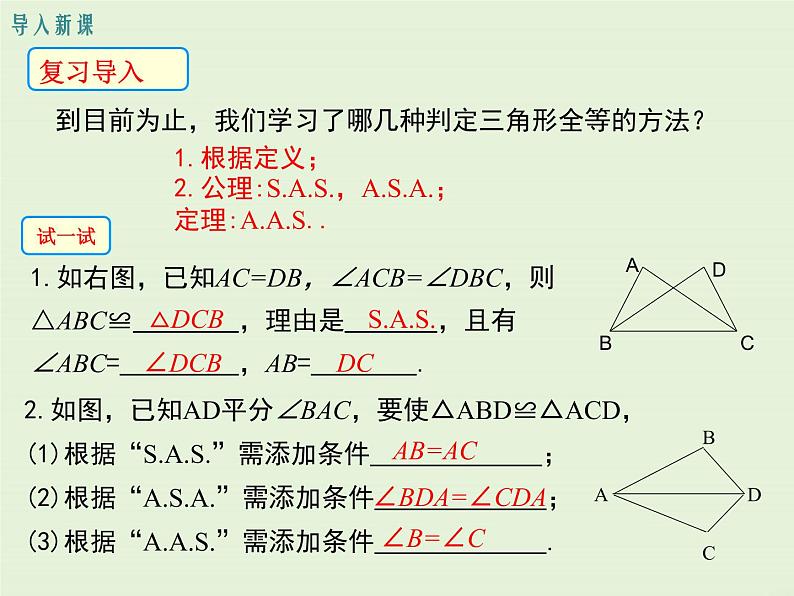
1.如右图,已知AC=DB,∠ACB=∠DBC,则△ABC≌ ,理由是 ,且有∠ABC= ,AB= .
2.如图,已知AD平分∠BAC,要使△ABD≌△ACD,(1)根据“”需添加条件 ;(2)根据“”需添加条件 ;(3)根据“”需添加条件 .
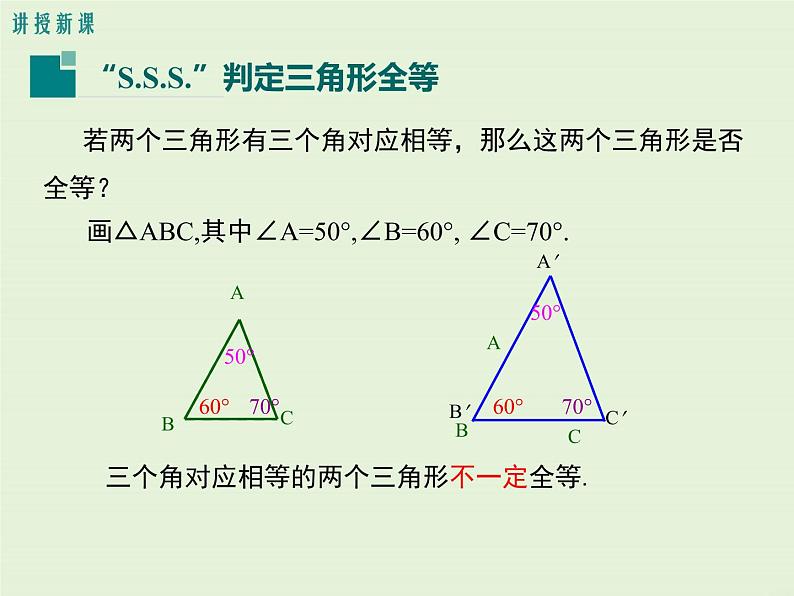
若两个三角形有三个角对应相等,那么这两个三角形是否全等?
画△ABC,其中∠A=50°,∠B=60°, ∠C=70°.
三个角对应相等的两个三角形不一定全等.
1.画一线段AB使它的长度等于c(4.5 cm).
2.以点A为圆心,以线段b(3cm)的长为半径画圆弧;以点B为圆心,以线段a(4cm)的长为半径画圆弧;两弧交于点C.
把你画的三角形与其他同学画的三角形相比较,它们全等吗?
如果两个三角形有三条边分别对应相等,那么这两个三角形是否一定全等呢?
如图,已知三条线段a,b,c,试画一个三角形,使这三条线段分别为其三边.
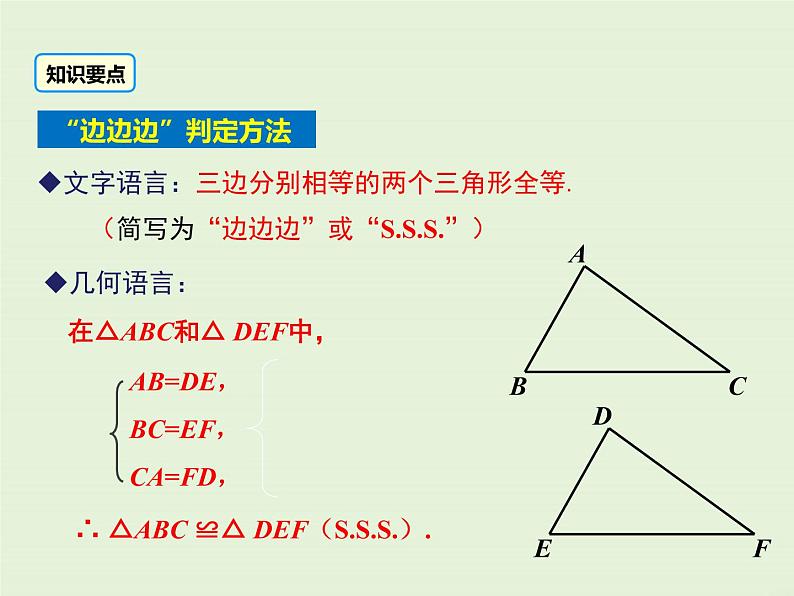
文字语言:三边分别相等的两个三角形全等. (简写为“边边边”或“”)
在△ABC和△ DEF中,
∴ △ABC ≌△ DEF().
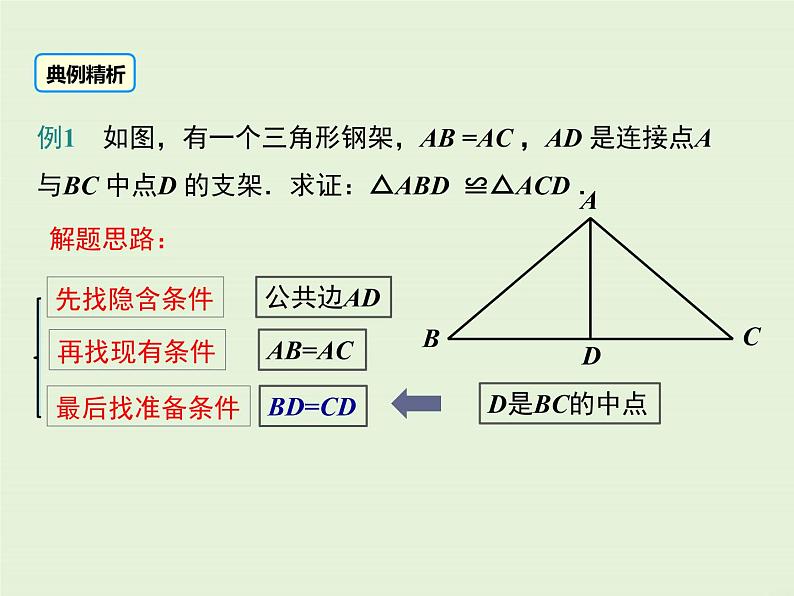
例1 如图,有一个三角形钢架,AB =AC ,AD 是连接点A 与BC 中点D 的支架.求证:△ABD ≌△ACD .
证明:∵ D 是BC中点, ∴ BD =DC. 在△ABD 与△ACD 中,
∴ △ABD ≌ △ACD ( ).
例2 如图,四边形ABCD中,AB=CD,AD=CB,求证:∠B=∠D
证明:在△ABC 和△CDA中, ∵ AB=CD(已知), BC=DA(已知), AC=CA(公共边), ∴ △ABC ≌ △CDA(). ∴∠B=∠D.
例3 已知: 如图,AC=AD ,BC=BD. 求证: ∠C=∠D.
判定三角形全等时最少有几组边对应相等?最多有几组边?
判定三角形全等时最少有几组角对应相等?最多有几组角?
解: △ABC≌△DCB. 理由如下: 在△ABC和△DCB, AB = DC, AC = DB, = ,
△ABC ≌ ( )
1.如图,AB=CD,AC=BD,△ABC和△DCB是否全等?请完成下列解题步骤.
2.如图,D、F是线段BC上的两点,AB=CE,AF=DE,要使 △ABF≌△ECD ,还需要条件 .
3.已知:如图,AC=FE,AD=FB,BC=DE.求证:(1)△ABC≌△FDE; (2) ∠C= ∠E.
证明:(1)∵ AD=FB, ∴AB=FD(等式性质). 在△ABC和△FDE 中,
AC=FE(已知),BC=DE(已知),AB=FD(已证),∴△ABC≌△FDE(SSS);
(2)∵ △ABC≌△FDE(已证),
∴ ∠C=∠E(全等三角形的对应角相等).
初中数学华师大版八年级上册5 边边边教学演示课件ppt: 这是一份初中数学华师大版八年级上册5 边边边教学演示课件ppt,共16页。PPT课件主要包含了创设情境引入新课,问题三,探究新知,归纳总结,学以致用,巩固提高练习,拓展延伸练习提升等内容,欢迎下载使用。
数学八年级上册5 边边边教学课件ppt: 这是一份数学八年级上册5 边边边教学课件ppt,共25页。PPT课件主要包含了知识要点,新知导入,填一填,全等三角形,课程讲授,不一定全等,分别相等,SSS,边边边,随堂练习等内容,欢迎下载使用。
八年级上册5 边边边课文ppt课件: 这是一份八年级上册5 边边边课文ppt课件,文件包含5边边边pptx、5边边边doc等2份课件配套教学资源,其中PPT共25页, 欢迎下载使用。













