初中数学人教版八年级上册13.3 等腰三角形综合与测试精品同步达标检测题

这是一份初中数学人教版八年级上册13.3 等腰三角形综合与测试精品同步达标检测题，共12页。试卷主要包含了5°．，5°，，5AD,等内容，欢迎下载使用。
《等腰三角形》解答题专练


LISTNUM OutlineDefault \l 3 如图所示，已知在△ABC中，AB=AD=DC，∠BAD=26°，求∠B和∠C的度数．























LISTNUM OutlineDefault \l 3 如图,△ABC中，AB=AC=5，AB的垂直平分线DE交AB、AC于E、D，


(1）若△BCD的周长为8，求BC的长；


(2）若∠ABD：∠DBC=1：1，求∠A的度数．




















LISTNUM OutlineDefault \l 3 如图，△ACB和△ADE均为等边三角形，点C、E、D在同一直线上，连接BD，试猜想线段CE、BD之间的数量关系，并说明理由.























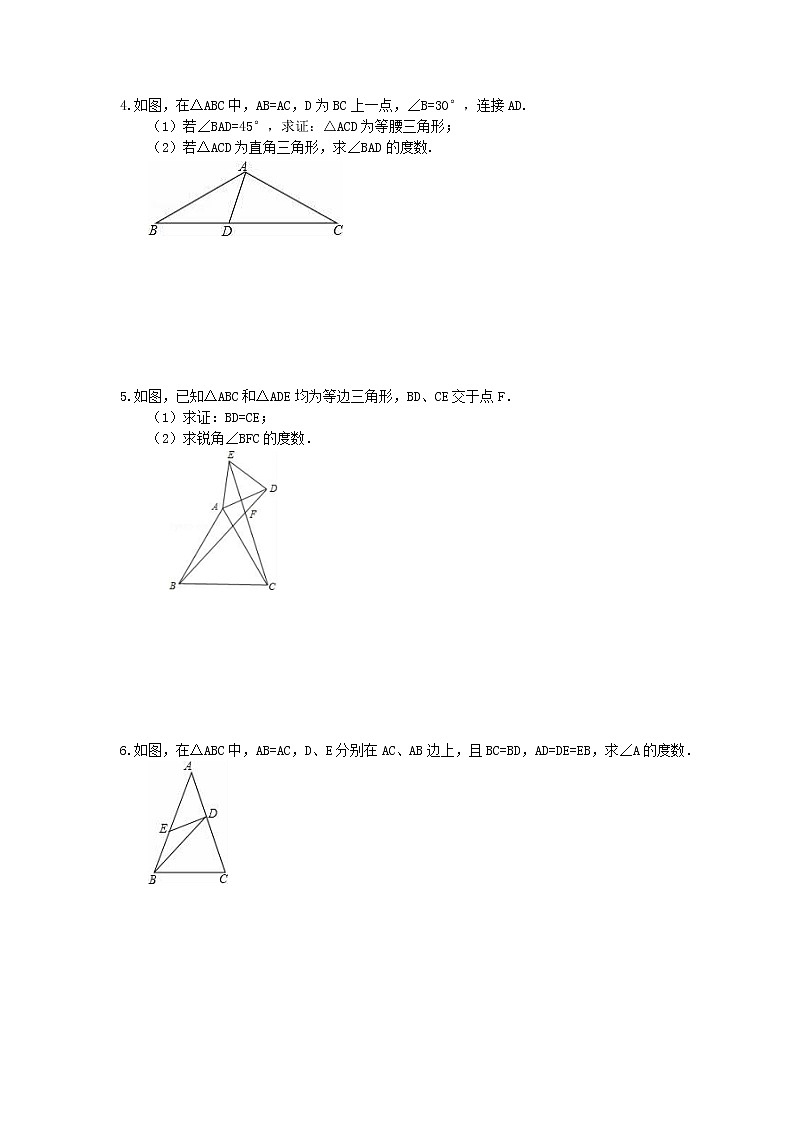
LISTNUM OutlineDefault \l 3 如图，在△ABC中，AB=AC，D为BC上一点，∠B=30°，连接AD.


（1）若∠BAD=45°，求证：△ACD为等腰三角形；


（2）若△ACD为直角三角形，求∠BAD的度数.


























LISTNUM OutlineDefault \l 3 如图，已知△ABC和△ADE均为等边三角形，BD、CE交于点F．


（1）求证：BD=CE；


（2）求锐角∠BFC的度数．


























LISTNUM OutlineDefault \l 3 如图，在△ABC中，AB=AC，D、E分别在AC、AB边上，且BC=BD，AD=DE=EB，求∠A的度数．


























LISTNUM OutlineDefault \l 3 如图，在△ABC中，AB=AC，AM平分∠BAC，交BC于点M，D为AC上一点，延长AB到点E，使CD=BE，连接DE，交BC于点F，过点D作DH∥AB，交BC于点H，G是CH的中点.


(1)求证：DF=EF.


(2)试判断GH，HF，BC之间的数量关系，并说明理由.



































LISTNUM OutlineDefault \l 3 如图1，在△ABC中，AB=AC，点D是BC的中点，点E在AD上．


（1）求证：BE=CE；


（2）如图2，若BE的延长线交AC于点F，且BF⊥AC，垂足为F，∠BAC=45°，原题设其它条件不变．求证：△AEF≌△BCF．












































LISTNUM OutlineDefault \l 3 如图：AD为△ABC的高，∠B=2∠C，用轴对称图形说明：CD=AB+BD．


























LISTNUM OutlineDefault \l 3 如图,已知ΔABC中,∠ACB=90°,CD⊥AB于D,BF平分∠ABC交CD于E,交AC于F.


求证：CE=CF．


























LISTNUM OutlineDefault \l 3 如图在△ABC中，AB=AC，∠BAC=120°，EF为AB的垂直平分线，EF交BC于点F，交AB于点E．求证：BF=FC．


























LISTNUM OutlineDefault \l 3 已知：如图，△ABC和△BDE都是等边三角形，且A，E，D三点在一直线上．


请你说明DA﹣DB=DC．





























LISTNUM OutlineDefault \l 3 如图，△ABC中，AB=AC，∠BAC=90°，CD平分∠ACB，BE⊥CD，垂足E在CD的延长线上，试探究线段BE和CD的数量关系，并证明你的结论．




































































LISTNUM OutlineDefault \l 3 如图，△ABC中，D是BC的中点，过D点的直线GF交AC于F，交AC的平行线BG于G点，DE⊥DF，交AB于点E，连结EG、EF．


（1）求证：BG=CF；


（2）请你判断BE+CF与EF的大小关系，并说明理由．





























LISTNUM OutlineDefault \l 3 综合与探究


两块等腰直角三角尺△ABC和△DEC如图所示摆放，其中∠ACB=∠DCE=90º,F是DE的中点，H是AE的中点，G是BD的中点.


⑴如图①，若点D，E分别在AC，BC的延长线上，通过观察和测量，猜想FH和FG的数量关系和位置关系,并证明你的猜想.


⑵如图②，若将三角尺△DEC绕着点C顺时针旋转至A，C，E在一条直线上时，其余条件均不变，则⑴中的猜想是否还成立，若成立，请加以证明；若不成立，请说明理由.


⑶如图③，将图①中的△DEC绕着点C顺时针旋转一个锐角，得到图③，⑴中的猜想还成立吗？请直接写出结论，不用证明.





























参考答案


LISTNUM OutlineDefault \l 3 \s 1 解：在△ABC中，AB=AD=DC，


∵AB=AD，在三角形ABD中，


∠B=∠ADB=（180°﹣26°）×=77°，


又∵AD=DC，在三角形ADC中，


∴∠C==77°×=38.5°．





LISTNUM OutlineDefault \l 3 ①3，②36°


LISTNUM OutlineDefault \l 3 解：CE=BD，


理由：∵△ACB和△ADE均为等边三角形，


∴AD=AE，AB=AC，∠DAE=∠BAC=60°，


∴∠DAE﹣∠BAE=∠BAC﹣∠BAE，


∴∠DAB=∠EAC.


在△ADB和△AEC中，，


∴△ADB≌△AEC（SAS），


∴CE=BD.





LISTNUM OutlineDefault \l 3 解：


（1）证明：∵AB=AC，∠B=30°，∴∠B=∠C=30°，


∴∠BAC=180°﹣30°﹣30°=120°，


∵∠BAD=45°，


∴∠CAD=∠BAC﹣∠BAD=120°﹣45°=75°，∠ADC=∠B+∠BAD=75°，


∴∠ADC=∠CAD，∴AC=CD，即△ACD为等腰三角形；


（2）解：有两种情况：


①当∠ADC=90°时，


∵∠B=30°，


∴∠BAD=∠ADC﹣∠B=90°﹣30°=60°；


②当∠CAD=90°时，


∠BAD=∠BAC﹣∠CAD=120°﹣90°=30°；


即∠BAD的度数是60°或30°.





LISTNUM OutlineDefault \l 3 （1）证明：∵△ABC和△ADE均为等边三角形，∴AE=AD、AB=AC，


又∵∠EAD=∠BAC=60°，∠EAD+∠DAC=∠BAC+∠DAC，即∠DAB=∠EAC，


在△EAC和△DAB中，，∴△EAC≌△DAB，即可得出BD=CE．


（2）解：由（1）△EAC≌△DAB，可得∠ECA=∠DBA，


又∵∠DBA+∠DBC=60°，在△BFC中，∠ECA+∠DBC=60°，∠ACB=60°，


则∠BFC=180°﹣∠ACB﹣（∠ECA+∠DBC）=180°﹣60°﹣60°=60°．








LISTNUM OutlineDefault \l 3 解：∵DE=EB∴设∠BDE=∠ABD=x，


∴∠AED=∠BDE+∠ABD=2x，


∵AD=DE，∴∠AED=∠A=2x，


∴∠BDC=∠A+∠ABD=3x，


∵BD=BC，


∴∠C=∠BDC=3x，


∵AB=AC，


∴∠ABC=∠C=3x，


在△ABC中，3x+3x+2x=180°，解得x=22.5°，


∴∠A=2x=22.5°×2=45°．








LISTNUM OutlineDefault \l 3











LISTNUM OutlineDefault \l 3 证明：（1）∵AB=AC，D是BC的中点，


∴∠BAE=∠EAC，


在△ABE和△ACE中，，


∴△ABE≌△ACE（SAS），


∴BE=CE；





（2）∵∠BAC=45°，BF⊥AF，


∴△ABF为等腰直角三角形，


∴AF=BF，


∵AB=AC，点D是BC的中点，


∴AD⊥BC，


∴∠EAF+∠C=90°，


∵BF⊥AC，


∴∠CBF+∠C=90°，


∴∠EAF=∠CBF，


在△AEF和△BCF中，，


∴△AEF≌△BCF（ASA）．





LISTNUM OutlineDefault \l 3 证明：在CD上取一点E使DE=BD，连接AE．





∵BD=DE，且∠AED为△AEC的外角，∠B=2∠C，


∴∠B=∠AED=∠C+∠EAC=2∠C，


∴∠EAC=∠C，


∴AE=EC；


则CD=DE+EC=AB+BD．





LISTNUM OutlineDefault \l 3 证明：


∵∠ACB＝90°,CD⊥AB


∴∠CBF＋∠CFB＝∠DBE＋∠DEB＝90°


∵BF平分∠ABC


∴∠CBF＝∠DBE


∵∠CBF＋∠CFB＝∠DBE＋∠DEB


∴∠CFB＝∠DEB


∵∠FEC＝∠DEB


∴∠CFB＝∠FEC


∴CE＝CF





LISTNUM OutlineDefault \l 3 证明：连接AF，





∵AB=AC，∠BAC=120°，


∴∠B=∠C=30°，


∵EF为AB的垂直平分线，


∴BF=AF，


∴∠BAF=∠B=30°，


∴∠FAC=120°﹣30°=90°，


∵∠C=30°，


∴AF=CF，


∵BF=AF，


∴BF=FC．





LISTNUM OutlineDefault \l 3 证明：△ABC和△BDE都是等边三角形，


∴AB=BC，BE=BD=DE（等边三角形的边相等），


∠ABC=∠EBD=60°（等边三角形的角是60°）．


∴∠ABC﹣∠EBC=∠EBD﹣∠EBC


∠ABE=CBD （等式的性质），


在△ABE和△CBD中，，


∴△ABE≌△CBD（SAS）


∴AE=DC（全等三角形的对应边相等）．


∵AD﹣DE=AE（线段的和差）


∴AD﹣BD=DC（等量代换）．





LISTNUM OutlineDefault \l 3 解：CD=2BE，理由为：延长BE交CA延长线于F，





∵CD平分∠ACB，∴∠FCE=∠BCE，


在△CEF和△CEB中，，


∴△CEF≌△CEB（ASA），


∴FE=BE，


∵∠DAC=∠CEF=90°，


∴∠ACD+∠F=∠ABF+∠F=90°，


∴∠ACD=∠ABF，


在△ACD和△ABF中，，


∴△ACD≌△ABF（ASA），


∴CD=BF，


∴CD=2BE．





LISTNUM OutlineDefault \l 3 解：（1）∵BG∥AC，


∴∠DBG=∠DCF．


∵D为BC的中点，


∴BD=CD


又∵∠BDG=∠CDF，在△BGD与△CFD中，


∵


∴△BGD≌△CFD（ASA）．


∴BG=CF．


（2）BE+CF＞EF．


∵△BGD≌△CFD，


∴GD=FD，BG=CF．


又∵DE⊥FG，


∴EG=EF（垂直平分线到线段端点的距离相等）．


∴在△EBG中，BE+BG＞EG，


即BE+CF＞EF．








2017年2月8日





、综合题


LISTNUM OutlineDefault \l 3 解：⑴猜想FH=FG,FH⊥FG.


证明：∵△ACB和△DCE都是等腰直角三角形，且∠ACB=∠DCE=90º，CD=CE,AC=BC,


∴A，C，D和B，C，E都在一条直线上，AD=BE.


∵F，H分别是DE，AE的中点，


∴FH∥AD,FH=0.5AD,


同理FG∥EB,FG=0.5EB.


∴FH=FG.


∵AD⊥BE，


∴FH⊥FG.


⑵成立.


证明：∵CE=CD,∠ECD=∠ACD=90º,AC=BC,


∴△ACD≌△BCE.


∴AD=BE，∠ADC=∠BEC.


由⑴知，FH=0.5AD,FH∥AD,FG=0.5BE,FG∥BE,


∴FH=FG.


延长AD交BE于点I.


∵∠ADC+∠CAD=90º,


∴∠BEC=∠CAD=90º.


∴∠AIE=90º


∴FH⊥FG.


∴⑴中的猜想成立.


⑶⑴中的猜想成立,结论是FH=FG，FH⊥FG.