初中数学人教版九年级上册24.2.2 直线和圆的位置关系优秀综合训练题

这是一份初中数学人教版九年级上册24.2.2 直线和圆的位置关系优秀综合训练题，共16页。试卷主要包含了5B．2C．2等内容，欢迎下载使用。

24.2.2《切线的判定和性质》专项练习


一．选择题


1．如图，在以点O为圆心的两个同心圆中，大圆的弦AB与小圆相切，切点为C，若大圆的半径是13，AB=24，则小圆的半径是（ ）





A．4B．5C．6D．7


2．如图，AB、AC、BD是⊙O的切线，切点分别为P、C、D，若AB=5，AC=3，则BD的长是（ ）





A．1.5B．2C．2.5D．3


3．如图，⊙O中，CD是切线，切点是D，直线CO交⊙O于B、A，∠A=20°，则∠C的度数是（ ）





A．25°B．65°C．50°D．75°


4．如图，直线AB与⊙O相切于点A，⊙O的半径为1，若∠OBA=30°，则OB长为（ ）





A．1B．2C．D．2


5．如图，∠NAM=30°，O为边AN上一点，以点O为圆心，2为半径作⊙O，交AN边于D、E两点，则当⊙O与AM相切时，AD等于（ ）





A．4B．3C．2D．1














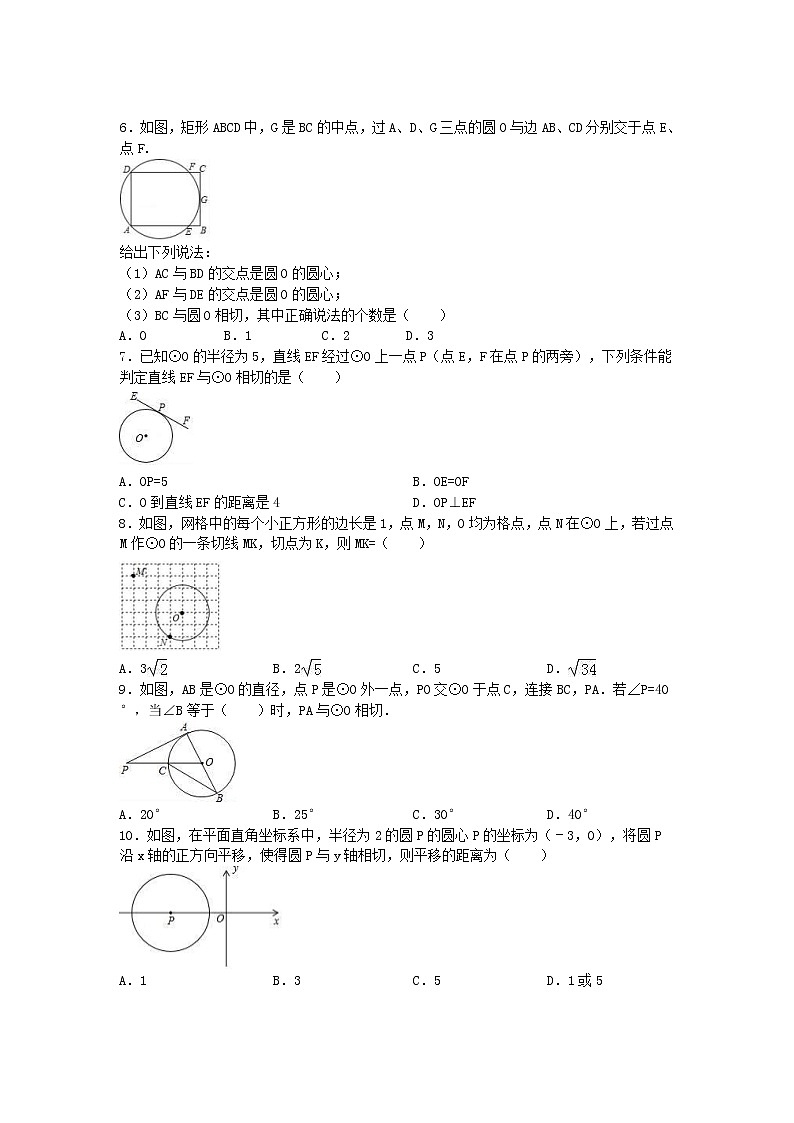
6．如图，矩形ABCD中，G是BC的中点，过A、D、G三点的圆O与边AB、CD分别交于点E、点F.





给出下列说法：


（1）AC与BD的交点是圆O的圆心；


（2）AF与DE的交点是圆O的圆心；


（3）BC与圆O相切，其中正确说法的个数是（ ）


A．0 B．1 C．2 D．3


7．已知⊙O的半径为5，直线EF经过⊙O上一点P（点E，F在点P的两旁），下列条件能判定直线EF与⊙O相切的是（ ）





A．OP=5B．OE=OF


C．O到直线EF的距离是4D．OP⊥EF


8．如图，网格中的每个小正方形的边长是1，点M，N，O均为格点，点N在⊙O上，若过点M作⊙O的一条切线MK，切点为K，则MK=（ ）





A．3B．2C．5D．


9．如图，AB是⊙O的直径，点P是⊙O外一点，PO交⊙O于点C，连接BC，PA．若∠P=40°，当∠B等于（ ）时，PA与⊙O相切．





A．20°B．25°C．30°D．40°


10．如图，在平面直角坐标系中，半径为2的圆P的圆心P的坐标为（﹣3，0），将圆P沿x轴的正方向平移，使得圆P与y轴相切，则平移的距离为（ ）





A．1B．3C．5D．1或5








11．如图，⊙O的半径为3，四边形ABCD是⊙O的内接四边形，∠A=60°，∠D=110°，的度数是70°，直线l与⊙O相切于点A．在没有滑动的情况下，将⊙O沿l向右滚动，使O点向右移动70π，则此时⊙O与直线l相切的切点所在的劣弧是（ ）





A．B．C．D．


12．如图，在等边△ABC中，点O在边AB上，⊙O过点B且分别与边AB、BC相交于点D、E、F是AC上的点，判断下列说法错误的是（ ）





A．若EF⊥AC，则EF是⊙O的切线


B．若EF是⊙O的切线，则EF⊥AC


C．若BE=EC，则AC是⊙O的切线


D．若BE=EC，则AC是⊙O的切线


13．如图，P为⊙O的直径BA延长线上的一点，PC与⊙O相切，切点为C，点D是⊙O上一点，连接PD．已知PC=PD=BC．





下列结论：（1）PD与⊙O相切；（2）四边形PCBD是菱形；（3）PO=CD；（4）弧AC=弧AD．


其中正确的个数为（ ）


A．1个B．2个C．3个D．4个


14．如图，直线l1∥l2，⊙O与l1和l2分别相切于点A和点B．直线MN与l1相交于M；与l2相交于N，⊙O的半径为1，∠1=60°，直线MN从如图位置向右平移，下列结论


①l1和l2的距离为2 ②MN=③当直线MN与⊙O相切时，∠MON=90°


④当AM+BN=时，直线MN与⊙O相切．正确的个数是（ ）





A．1B．2C．3D．4





15．如图，直线AB、CD相交于点O，∠AOD=30°，半径为1cm的⊙P的圆心在射线OA上，且与点O的距离为6cm．如果⊙P以1cm/s的速度沿由A向B的方向移动，那么（ ）秒钟后⊙P与直线CD相切．





A．4B．8C．4或6D．4或8





二．填空题


16．在平面直角坐标系中，点P的坐标为（﹣4，0），半径为1的动圆⊙P沿x轴正方向运动，若运动后⊙P与y轴相切，则点P的运动距离为 ．





17．如图，直线PA是⊙O的切线，AB是过切点A的直径，连接PO交⊙O于点C，连接BC，若∠ABC=25°，则∠P的度数为 ．





18．如图，已知PA、PB是⊙O的切线，A、B分别为切点，∠OAB=30°．


（1）∠APB= ；


（2）当OA=2时，AP= ．





19．如图所示，直线y=x﹣2与x轴、y轴分别交于M，N两点，⊙O的半径为1，将⊙O以每秒1个单位的速度向右作平移运动，当移动 s时，直线MN恰好与圆O相切．











20．如图，在平面直角坐标系xOy中，半径为2的⊙P的圆心P的坐标为（﹣3，0），将⊙P沿x轴正方向以0.5个单位/秒的速度平移，使⊙P与y轴相切，则平移的时间为 秒．





21．已知，如图，AB是⊙O的直径，点P在BA的延长线上，弦CD交AB于E，连接OD、PC、BC，∠AOD=2∠ABC，∠P=∠D，过E作弦GF⊥BC交圆于G、F两点，连接CF、BG．





则下列结论：


①CD⊥AB；②PC是⊙O的切线；③OD∥GF；④弦CF的弦心距等于BG．


则其中正确的是 （只需填序号）





三．解答题


22．如图，AB是半圆O的直径，C是半圆O上的一点，CF切半圆O于点C，BD⊥CF于为点D，BD与半圆O交于点E．


（1）求证：BC平分∠ABD．


（2）若DC=8，BE=4，求圆的直径．















































23．如图，一圆与平面直角坐标系中的x轴切于点A（8，0），与y轴交于点B（0，4），C（0，16），求该圆的直径．





























24．如图，在△ABC中，AB=AC，∠A=30°，以AB为直径的⊙O交BC于点D，交AC于点E，连结DE，过点B作BP平行于DE，交⊙O于点P，连结EP、CP、OP．


（1）BD=DC吗？说明理由；


（2）求∠BOP的度数；


（3）求证：CP是⊙O的切线．




















25．如图，▱ABCD中，⊙O过点A、C、D，交BC于E，连接AE，∠BAE=∠ACE．


（1）求证：AE=CD；


（2）求证：直线AB是⊙O的切线．




















26．已知AB是⊙O的直径，AP是⊙O的切线，A是切点，BP与⊙O交于点C．


（1）如图①，若∠P=35°，求∠ABP的度数；


（2）如图②，若D为AP的中点，求证：直线CD是⊙O的切线．



































27．如图（1），在△ABC中，∠ACB=90°，以AB为直径作⊙O；过点C作直线CD交AB的延长线于点D，且BD=OB，CD=CA．


（1）求证：CD是⊙O的切线．


（2）如图（2），过点C作CE⊥AB于点E，若⊙O的半径为8，∠A=30°，求线段BE．





















































28．如图，在△ABC中，∠C=90°，∠ABC的平分线BE交AC于点E，过点E作直线


BE的垂线交AB于点F，⊙O是△BEF的外接圆．


（1）求证：AC是⊙O的切线；


（2）过点E作EH⊥AB于点H，求证：EF平分∠AEH；


（3）求证：CD=HF．




















29．如图，已知A是⊙O上一点，半径OC的延长线与过点A的直线交于点B，OC=BC，AC=OB．


（1）求证：AB是⊙O的切线；


（2）若∠ACD=45°，OC=2，求弦CD的长．




















30．如图，AB是半径为2的⊙O的直径，直线m与AB所在直线垂直，垂足为C，OC=3，点P是⊙O上异于A、B的动点，直线AP、BP分别交m于M、N两点．


（1）当点C为MN中点时，连接OP，PC，判断直线PC与⊙O是否相切并说明理由．


（2）点P是⊙O上异于A、B的动点，以MN为直径的动圆是否经过一个定点，若是，请确定该定点的位置；若不是，请说明理由．








参考答案


1．B．


2．B．


3．C．


4．B．


5．C．


6．C．


7．D．


8．B．


9．B．


10．C．


12．C．


13．C．


14．D．


15．D．


16．答案为3或5．


17．答案为：40°．


18．答案为：60°．


（2）答案为：2．


19．答案为：2﹣或2+．


20．答案为2或10


21．答案为：①②④．


22．（1）证明：连结OC，如图，


∵CD为切线，


∴OC⊥CD，


∵BD⊥DF，


∴OC∥BD，


∴∠1=∠3，


∵OB=OC，


∴∠1=∠2，


∴∠2=∠3，


∴BC平分∠ABD；


（2）解：连结AE交OC于G，如图，


∵AB为直径，


∴∠AEB=90°，


∵OC∥BD，


∴OC⊥CD，


∴AG=EG，


易得四边形CDEG为矩形，


∴GE=CD=8，


∴AE=2EG=16，


在Rt△ABE中，AB==4，


即圆的直径为4．





23．解：过圆心O′作y轴的垂线，垂足为D，连接O′A，


∵O′D⊥BC，


∴D为BC中点，


∴BC=16﹣4=12，OD=6+4=10，


∵⊙O′与x轴相切，


∴O′A⊥x轴，


∴四边形OAO′D为矩形，


半径O′A=OD=10，





24．解：（1）BD=DC．理由如下：连接AD，


∵AB是直径，


∴∠ADB=90°，


∴AD⊥BC，


∵AB=AC，


∴BD=DC；


（2）∵AD是等腰△ABC底边上的中线，


∴∠BAD=∠CAD，


∴，


∴BD=DE．


∴BD=DE=DC，


∴∠DEC=∠DCE，


△ABC中，AB=AC，∠A=30°，


∴∠DCE=∠ABC=（180°﹣30°）=75°，


∴∠DEC=75°，


∴∠EDC=180°﹣75°﹣75°=30°，


∵BP∥DE，


∴∠PBC=∠EDC=30°，


∴∠ABP=∠ABC﹣∠PBC=75°﹣30°=45°，


∵OB=OP，


∴∠OBP=∠OPB=45°，


∴∠BOP=90°；


（3）设OP交AC于点G，如图，则∠AOG=∠BOP=90°，


在Rt△AOG中，∠OAG=30°，


∴=，


又∵==，


∴=，


∴=，


又∵∠AGO=∠CGP，


∴△AOG∽△CPG，


∴∠GPC=∠AOG=90°，


∴OP⊥PC，


∴CP是⊙O的切线；





25．解：（1）∵四边形ABCD是平行四边形


∴AB=CD，∠B=∠ADC


∵四边形ADCE是⊙O内接四边形


∴∠ADC+∠AEC=180°


∵∠AEC+∠AEB=180°


∴∠ADC=∠AEB


∴∠B=∠AEB


∴AE=CD


（2）如图：连接AO，并延长AO交⊙O交于点F，连接EF．





∵AF是直径


∴∠AEF=90°


∴∠AFE+∠EAF=90°


∵∠BAE=∠ECA，∠AFE=∠ACE


∴∠AFE=∠BAE


∴∠BAE+∠EAF=90°


∴∠BAF=90°且AO是半径


∴直线AB是⊙O的切线





26．（1）解：∵AB是⊙O的直径，AP是⊙O的切线，


∴AB⊥AP，


∴∠BAP=90°；


又∵∠P=35°，


∴∠AB=90°﹣35°=55°．


（2）证明：如图，连接OC，OD、AC．


∵AB是⊙O的直径，


∴∠ACB=90°（直径所对的圆周角是直角），


∴∠ACP=90°；


又∵D为AP的中点，


∴AD=CD（直角三角形斜边上的中线等于斜边的一半）；


在△OAD和△OCD中，


，


∴△OAD≌△OCD（SSS），


∴∠OAD=∠OCD（全等三角形的对应角相等）；


又∵AP是⊙O的切线，A是切点，


∴AB⊥AP，


∴∠OAD=90°，


∴∠OCD=90°，即直线CD是⊙O的切线．


27．（1）证明：如图1，连结OC，


∵点O为直角三角形斜边AB的中点，


∴OC=OA=OB．


∴点C在⊙O上，


∵BD=OB，


∴AB=DO，


∵CD=CA，


∴∠A=∠D，


∴△ACB≌△DCO，


∴∠DCO=∠ACB=90°，


∴CD是⊙O的切线；


（2）解：如图2，在Rt△ABC中，BC=ABsin∠A=2×8×sin30°=8，


∵∠ABC=90°﹣∠A=90°﹣30°=60°，


∴BE=BCcs60°=8×=4．











28．（1）证明：（1）如图，连接OE．


∵BE⊥EF，∴∠BEF=90°，


∴BF是圆O的直径，


∴OB=OE，


∴∠OBE=∠OEB，


∵BE平分∠ABC，


∴∠CBE=∠OBE，


∴∠OEB=∠CBE，


∴OE∥BC，


∴∠AEO=∠C=90°，


∴AC是⊙O的切线；


（2）证明：∵∠C=∠BHE=90°，∠EBC=∠EBA，


∴BEC=∠BEH，


∵BF是⊙O是直径，


∴∠BEF=90°，


∴∠FEH+∠BEH=90°，∠AEF+∠BEC=90°，


∴∠FEH=∠FEA，


∴FE平分∠AEH．


（3）证明：如图，连结DE．


∵BE是∠ABC的平分线，EC⊥BC于C，EH⊥AB于H，


∴EC=EH．


∵∠CDE+∠BDE=180°，∠HFE+∠BDE=180°，


∴∠CDE=∠HFE，


∵∠C=∠EHF=90°，


∴△CDE≌△HFE（AAS），


∴CD=HF，





29．解：（1）如图，连接OA；


∵OC=BC，AC=OB，


∴OC=BC=AC=OA．


∴△ACO是等边三角形．


∴∠O=∠OCA=60°，


∵AC=BC，


∴∠CAB=∠B，


又∠OCA为△ACB的外角，


∴∠OCA=∠CAB+∠B=2∠B，


∴∠B=30°，又∠OAC=60°，


∴∠OAB=90°，


∴AB是⊙O的切线；


（2）解：作AE⊥CD于点E，


∵∠O=60°，


∴∠D=30°．


∵∠ACD=45°，AC=OC=2，


∴在Rt△ACE中，CE=AE=；


∵∠D=30°，


∴AD=2，


∴DE=AE=，


∴CD=DE+CE=+．





30．解：（1）直线PC与⊙O相切，


理由是：如图1，∵AC⊥MN，


∴∠ACM=90°，


∴∠A+∠AMC=90°，


∵AB是⊙O的直径，


∴∠APB=∠NPM=90°，


∴∠PNM+∠AMC=90°=∠A+∠ABP，


∴∠ABP=∠AMC，


∵OP=OB，


∴∠ABP=∠OPB，


Rt△PMN中，C为MN的中点，


∴PC=CN，


∴∠PNM=∠NPC，


∴∠OPC=∠OPB+∠NPC=∠ABP+∠PNM=∠AMC+∠PNM=90°，


即OP⊥PC，


∴直线PC与⊙O相切；


（2）如图2，设该圆与AC的交点为D，连接DM、DN，


∵MN为直径，


∴∠MDN=90°，


则∠MDC+∠NDC=90°，


∵∠DCM=∠DCN=90°，


∴∠MDC+∠DMC=90°，


∴∠NDC=∠DMC，


则△MDC∽△DNC，


∴，即DC2=MC•NC


∵∠ACM=∠NCB=90°，∠A=∠BNC，


∴△ACM∽△NCB，


∴，即MC•NC=AC•BC；


即AC•BC=DC2，


∵AC=AO+OC=2+3=5，BC=3﹣2=1，


∴DC2=5，


∴DC=，


∵MN⊥DD'，


∴D'C=DC=，


∴以MN为直径的一系列圆经过两个定点D和D'，此定点在C的距离都是．