
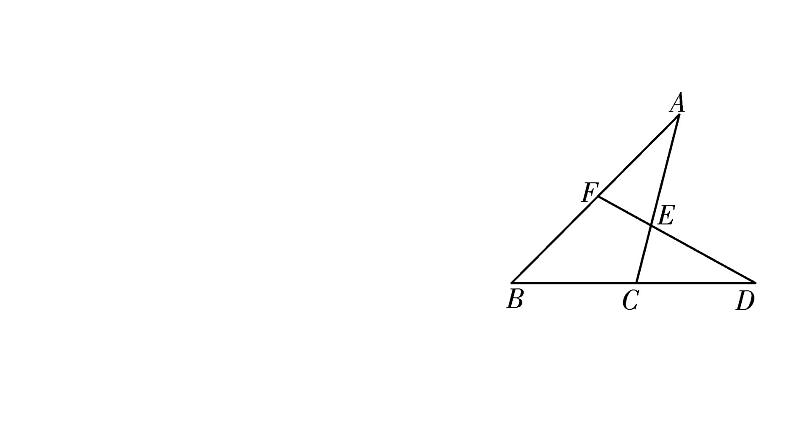
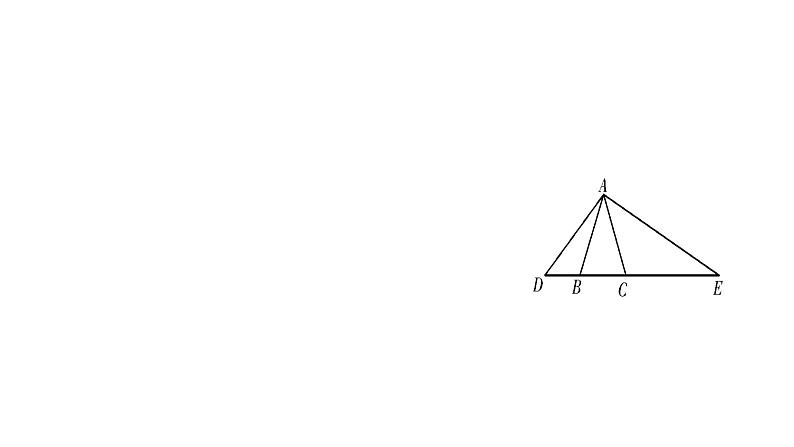
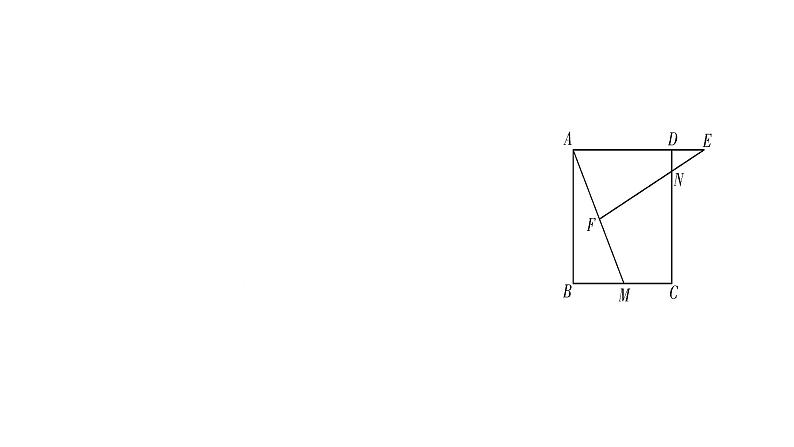
北师大版九年级上册4 探索三角形相似的条件习题课件ppt
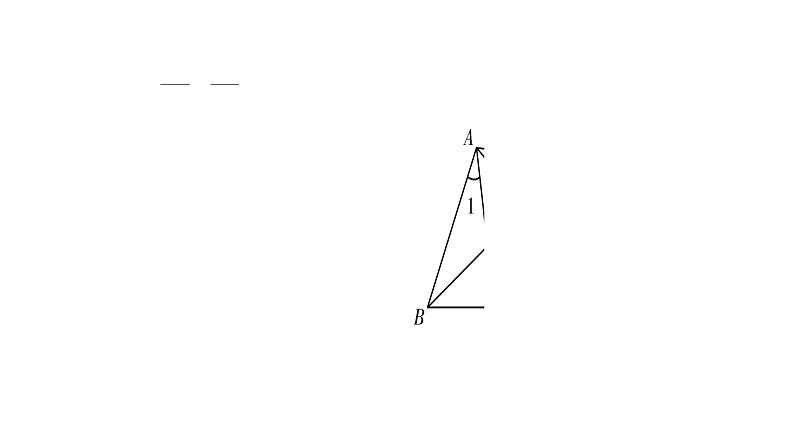
展开10.已知:如图S4-4-3,在△ABC中,AD=DB,∠1=∠2. 求证:△ABC∽△EAD.
证明:∵DB=AD,∴∠B=∠BAD. ∵∠BDA=∠1+∠C=∠2+∠ADE,∠1=∠2,∴∠C=∠ADE. ∴△ABC∽△EAD(两角分别相等的两个三角形相似).
11.如图S4-4-5,在△ABC中,∠C=90°,DM⊥AB于点M,DN⊥BC于点N,交AB于点E.求证:△DME∽△BCA.
证明:∵∠C=90°,DM⊥AB于点M,DN⊥BC于点N,∴∠C=∠ENB=∠DME=90°.∴AC∥DN.∴∠BEN=∠A.∵∠BEN=∠DEM,∴∠DEM=∠A.又∵∠DME=∠C,∴△DME∽△BCA.
12.如图S4-4-6,在△ABC中,AB=AC,点D,E分别在BC,AB上,且∠BDE=∠CAD. 求证:△ADE∽△ABD.
证明:∵AB=AC,∴∠B=∠C.∵∠ADB=∠C+∠CAD=∠BDE+∠ADE,∠BDE=∠CAD,∴∠ADE=∠C.∴∠B=∠ADE.∵∠DAE=∠BAD,∴△ADE∽△ABD.
13.如图S4-4-13,点C是线段AB上一点,△ACD和△BCE都是等边三角形,连接AE,BD,设AE交CD于点F. (1)求证:△ACE≌△DCB;(2)求证:△ADF∽△BAD.
证明:(1)∵△ACD和△BCE都是等边三角形,∴AC=CD,CE=CB,∠ACD=∠BCE=60°.∴∠ACE=∠DCB=120°. (2)∵△ACE≌△DCB,∵∠ADC=∠CAD=∠ACD=∠CBE=60°,∴DC∥BE.∴∠CAE=∠DBE.又∵∠DFA=∠ACD+∠CAE,∠ADB=∠ADC+∠CDB,∴∠DFA=∠ADB.
∴△ACE≌△DCB(SAS).
∴∠CAE=∠CDB.
∴△ADF∽△BAD.
∴∠CDB=∠DBE.
∴∠DAF=∠DBA.
14.如图S4-4-12,点D在等边△ABC的BC边上,△ADE为等边三角形,DE与AC交于点F. (1)证明:△ABD∽△DCF;(2)除了△ABD∽△DCF外,请写出图中其他所有的相似三角形.
(2)解:图中相似三角形有△AEF∽△DCF,△ABD∽△AEF,△ABC∽△ADE,△ADF∽△ACD.
(1)证明:如答图S4-4-1,
∵△ABC,△ADE为等边三角形,
∴∠B=∠C=∠3=60°.
∴∠1+∠2=∠DFC+∠2=180°-60°.
∴△ABD∽△DCF.
15.如图S4-4-16,在正三角形ABC中,D,E分别在边AC,AB上,且 ,AE=EB. 求证:△AED∽△CBD.
证明:∵△ABC为正三角形,∴∠A=∠C=60°,BC=AB. ∵AE=BE,∴CB=2AE. ∵ ,∴CD=2AD. ∴ . 而∠A=∠C,∴△AED∽△CBD.
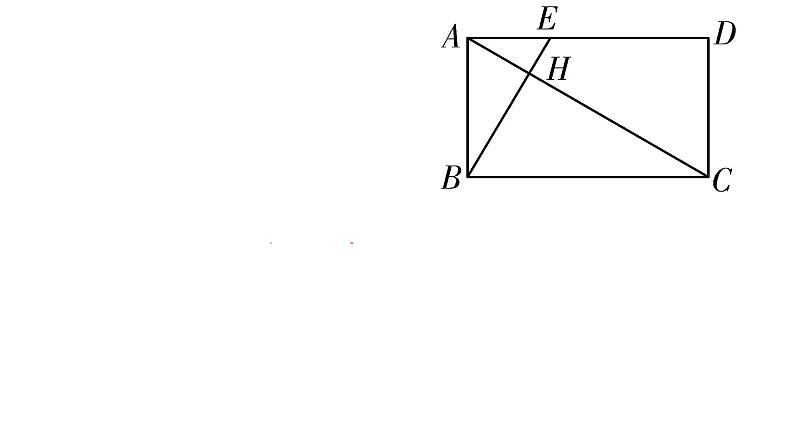
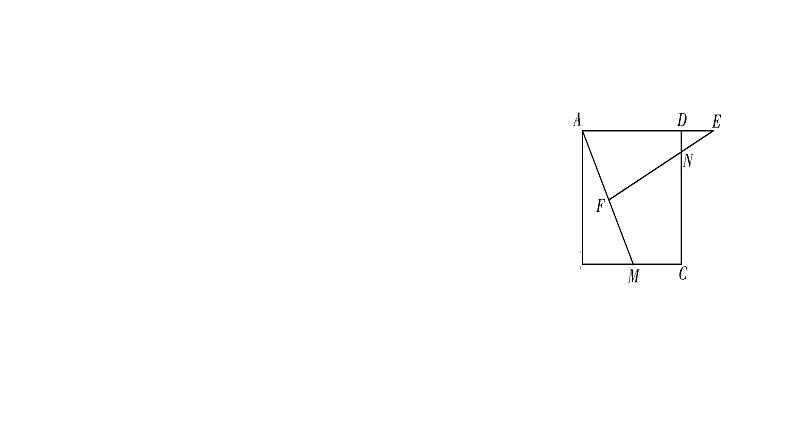
16.如图S4-4-17,在正方形ABCD中,已知点P是BC边上的点,且BP=3PC,点Q是CD的中点,试判断△ADQ∽△QCP是否成立,并说明理由.
解:成立.理由如下.设PC=a,则BP=3a,BC=4a.∵点Q是CD的中点,∴DQ=QC= CD=2a.∴ =2, =2.∴ .又∵∠D=∠C=90°,∴△ADQ∽△QCP.
证明:∵AD·AB=AF·AC,∴又∵∠A=∠A,∴△ABF∽△ACD.∴∠B=∠C,∠AFB=∠ADC.∴∠EFC=∠BDE.∴△DEB∽△FEC.
17.已知:如图S4-4-19,AD·AB=AF·AC.求证:△DEB∽△FEC.
18.如图S4-4-28,在△AOB中,∠AOB=90°,OA=12 cm,AB= cm,点P从O开始沿OA边向点A以2 cm/s的速度移动;点Q从点B开始沿BO边向点O以1 cm/s的速度移动,如果P,Q同时出发,用x s表示时间(0≤x≤6),那么:(1)点Q运动多少秒时,△OPQ的面积为5 cm2?(2)当x为何值时,以P,O,Q为顶点的三角形与△AOB相似?
解:(1)∵∠AOB=90°,∴BO2=AB2-AO2.∴BO=6.在Rt△OPQ中,OQ=6-x,OP=2x,∵△OPQ的面积为5 cm2,∴ OQ·OP=5,即 (6-x)·2x=5.解得x1=1,x2=5.即当Q运动1 s或5 s时,△OPQ的面积为5 cm2.
2)当△OPQ∽△OAB时, ,解得x=3 s;当△OPQ∽△OBA, ,解得x= s. 综上所述,当x=3 s或 s时,以P,O,Q为顶点的三角形与△AOB相似.
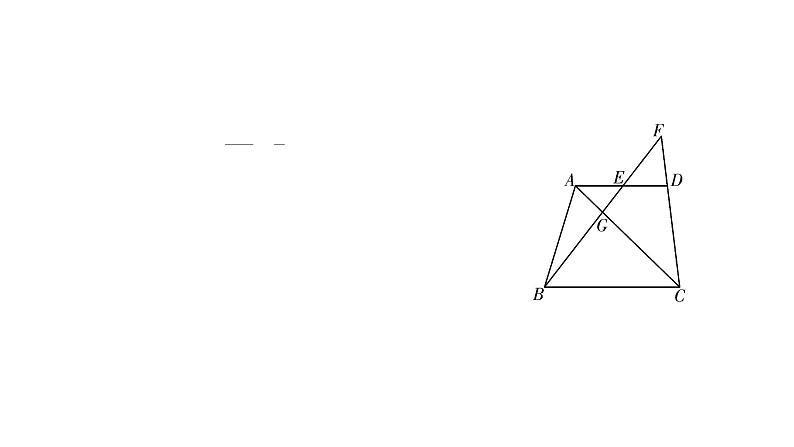
19.如图S4-4-39,在四边形ABCD中,AC,BD相交于点F,点E在BD上,且 (1)试问:∠BAE与∠CAD相等吗?为什么?(2)试判断△ABE与△ACD是否相似?并说明理由.
解:(1)∠BAE与∠CAD相等. 理由:∵ ∴△ABC∽△AED.∴∠BAC=∠EAD.∴∠BAE=∠CAD.(2)△ABE与△ACD相似. 理由如下:∵ ∴ 在△ABE与△ACD中,∵ ∠BAE=∠CAD,∴△ABE∽△ACD.
20.如图S4-4-37,已知 求证:∠ABD=∠CBE.
解:∵∴△ABC∽△DBE.∴∠ABC=∠DBE.∴∠ABC-∠DBC=∠DBE-∠DBC,即∠ABD=∠CBE.
20.已知,如图S4-4-38, 那么△ABD与△BCE相似吗?为什么?
解:相似.∵∴△ABC∽△DBE.∴∠ABC=∠DBE.∴∠ABC-∠DBC=∠DBE-∠DBC,即∠ABD=∠CBE.∵ ∴△ABD∽△CBE.
21.如图S4-4-43,以长为2的定线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上. (1)求AM,DM的长;(2)点M是AD的黄金分割点吗?为什么?
解:(1)在Rt△APD中,AP=1,AD=2,由勾股定理知PD=∴AM=AF=PF-AP=PD-AP= -1,DM=AD-AM=3- . 故AM的长为 -1,DM的长为3- .(2)点M是AD的黄金分割点. ∵∴点M是AD的黄金分割点.
北师大版4 探索三角形相似的条件优质课件ppt: 这是一份北师大版4 探索三角形相似的条件优质课件ppt,共27页。PPT课件主要包含了学习目标,导入新课,讲授新课,计算黄金比,雕塑--维纳斯,黄金分割的魅力,巴黎圣母院,联合国总部大厦,古埃及胡夫金字塔,古希腊巴特农神庙等内容,欢迎下载使用。
北师大版九年级上册4 探索三角形相似的条件精品ppt课件: 这是一份北师大版九年级上册4 探索三角形相似的条件精品ppt课件,共19页。PPT课件主要包含了学习目标,导入新课,讲授新课,SSS,几何语言,练一练,当堂检测,证明∵,课堂小结等内容,欢迎下载使用。
初中北师大版第四章 图形的相似4 探索三角形相似的条件完整版ppt课件: 这是一份初中北师大版第四章 图形的相似4 探索三角形相似的条件完整版ppt课件,共23页。PPT课件主要包含了学习目标,全等三角形,讲授新课,那这样变化一下呢,相似三角形,对应角,对应边,全等是一种特殊的相似,角边角,ASA等内容,欢迎下载使用。













