数学八年级上册第十二章 全等三角形综合与测试精品课时训练

这是一份数学八年级上册第十二章 全等三角形综合与测试精品课时训练，共16页。试卷主要包含了下列说法中，正确的是等内容，欢迎下载使用。




一．选择题


1．下列说法中，正确的是（ ）


A．面积相等的两个图形是全等图形


B．形状相等的两个图形是全等图形


C．周长相等的两个图形是全等图形


D．全等图形的面积相等


2．如图，△ABC≌△CDA，则下列结论错误的是（ ）





A．AC＝CAB．AB＝ADC．∠ACB＝∠CADD．∠B＝∠D


3．如图，∠BAD＝∠BCD＝90°，AB＝CB，据此可以证明△BAD≌△BCD，证明的依据是（ ）





A．AASB．ASAC．SASD．HL


4．如图所示，在△ABC中，D，E分别是边AC，BC上的点，若△ADB≌△EDB≌△EDC，则∠C的度数为（ ）





A．15°B．20°C．25°D．30°


5．如图，在△PAB中，∠A＝∠B，M、N、K分别是PA、PB、AB上的点，且AM＝BK，BN＝AK，若∠MKN＝40°，则∠P的度数为（ ）





A．100°B．110°C．80°D．90°


6．如图，在△ABC中，点D、E、F分别是BC、AB、AC上的点，若AB＝AC，BE＝CD，BD＝CF，∠EDF＝54°，则∠A的度数为（ ）





A．54°B．72°C．80°D．108°


7．某同学把一块三角形的玻璃打碎了3块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的方法是（ ）





A．带①去B．带②去C．带③去D．带①②③去


8．三条公路将A、B、C三个村庄连成一个如图的三角形区域，如果在这个区域内修建一个集贸市场，要使集贸市场到三条公路的距离相等，那么这个集贸市场应建的位置是（ ）





A．三条高线的交点B．三条中线的交点


C．三条角平分线的交点D．三边垂直平分线的交点


9．如图，把两根钢条AB，CD的中点O连在一起，可以做成一个测量工件内槽宽的工具（卡钳）．只要量得AC之间的距离，就可知工件的内径BD．其数学原理是利用△AOC≌△BOD，判断△AOC≌△BOD的依据是（ ）





A．SASB．SSSC．ASAD．AAS


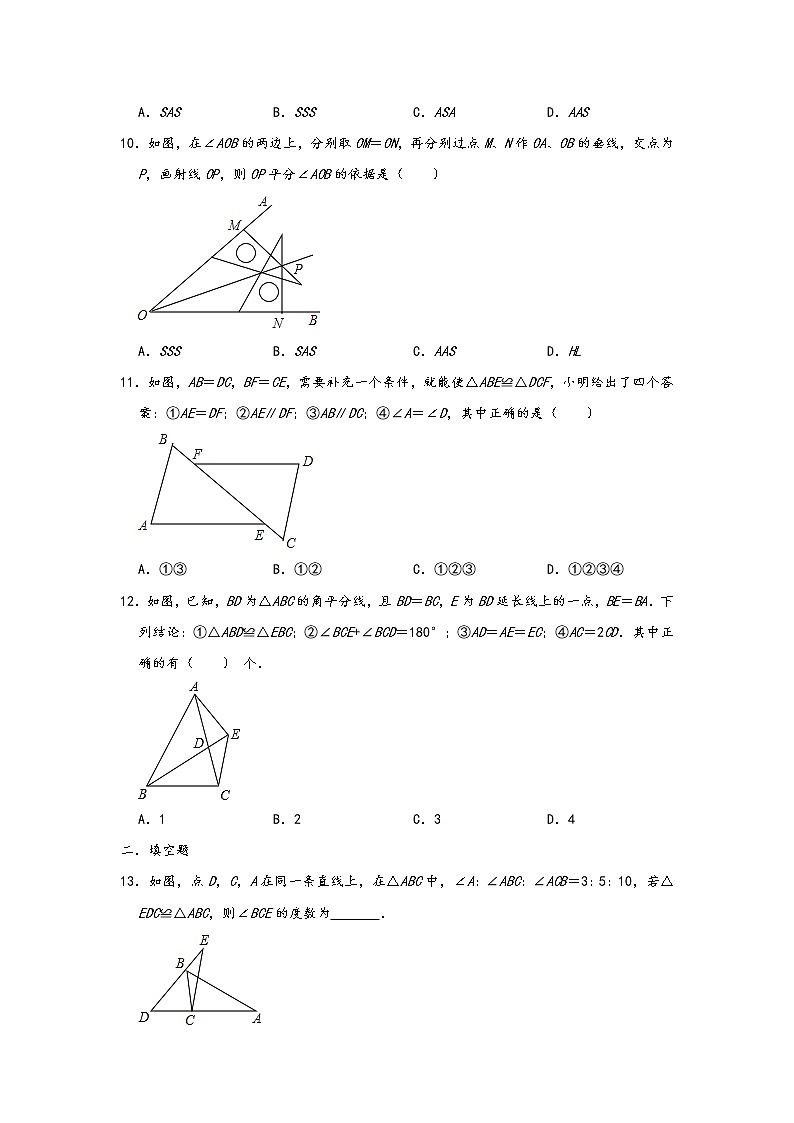
10．如图，在∠AOB的两边上，分别取OM＝ON，再分别过点M、N作OA、OB的垂线，交点为P，画射线OP，则OP平分∠AOB的依据是（ ）





A．SSSB．SASC．AASD．HL


11．如图，AB＝DC，BF＝CE，需要补充一个条件，就能使△ABE≌△DCF，小明给出了四个答案：①AE＝DF；②AE∥DF；③AB∥DC；④∠A＝∠D，其中正确的是（ ）





A．①③B．①②C．①②③D．①②③④


12．如图，已知，BD为△ABC的角平分线，且BD＝BC，E为BD延长线上的一点，BE＝BA．下列结论：①△ABD≌△EBC；②∠BCE+∠BCD＝180°；③AD＝AE＝EC；④AC＝2CD．其中正确的有（ ） 个．





A．1B．2C．3D．4


二．填空题


13．如图，点D，C，A在同一条直线上，在△ABC中，∠A：∠ABC：∠ACB＝3：5：10，若△EDC≌△ABC，则∠BCE的度数为 ．





14．已知△ABC≌△DEF，∠B＝120°，∠F＝35°．则∠D＝ 度．


15．如图，△ABC的两条高AD，BE相交于点F，请添加一个条件，使得△ADC≌△BEC（不添加其他字母及辅助线），你添加的条件是 ．





16．如图，△ABC的三条角平分线交于点O，O到AB的距离为3，且△ABC的周长为18，则△ABC的面积为 ．





17．如图，∠ACB＝90°，AC＝BC，BE⊥CE，AD⊥CE，垂足分别为E，D，AC＝13，BE＝5，则DE＝ ．





18．如图，小敏做了一个角平分仪ABCD，其中AB＝AD，BC＝DC，将仪器上的点A与∠PRQ的顶点R重合，调整AB和AD，使它们分别落在角的两边上，过点A，C画一条射线AE，AE就是∠PRQ的平分线．此角平分仪的画图原理是：根据仪器结构，可得△ABC≌△ADC，这样就有∠QAE＝∠PAE．则说明这两个三角形全等的依据是 ．





19．如图为6个边长相等的正方形的组合图形，则∠1+∠2+∠3＝ ．








三．解答题


20．如图，四边形ABCD中，AD∥BC，AB＝DC＝AD，BD＝AC，BD、AC相交于点O．


（1）求证：△ABO≌△DCO；


（2）写出图中所有与∠ACB相等的角．





21．如图，在线段BC上有两点E，F，在线段CB的异侧有两点A，D，满足AB＝CD，AE＝DF，CE＝BF，连接AF；


（1）求证：∠B＝∠C；


（2）若∠B＝40°，∠DFC＝30°，当AF平分∠BAE时，求∠BAF．





22．如图，在△ABC中，AB＝AC＝2，∠B＝36°，点D在线段BC上运动（点D不与点B、C重合），连接AD，作∠ADE＝36°，DE交线段AC于点E．


（1）当∠BDA＝128°时，∠EDC＝ ，∠AED＝ ；


（2）线段DC的长度为何值时，△ABD≌△DCE？请说明理由；


（3）在点D的运动过程中，△ADE的形状可以是等腰三角形吗？若可以，请直接写出∠BDA的度数；若不可以，请说明理由．





23．如图，△ADC中，DB是高，点E是DB上一点，AB＝DB，EB＝CB，M，N分别是AE，CD上的点，且AM＝DN．


（1）求证：△ABE≌△DBC．


（2）探索BM和BN的关系，并证明你的结论．














24．已知，在△ABC中，AC＝BC．分别过A，B点作互相平行的直线AM和BN．过点C的直线分别交直线AM，BN于点D，E．





（1）如图1．若CD＝CE．求∠ABE的大小；


（2）如图2．∠ABC＝∠DEB＝60°．求证：AD+DC＝BE．





参考答案


一．选择题


1．解：A、面积相等，但图形不一定能完全重合，故本选项错误；


B、形状相等的两个图形不一定能完全重合，故本选项错误；


C、周长相等的两个图形不一定能完全重合，故本选项错误；


D、全等图形的面积相等，故本选项正确．


故选：D．


2．解：A、由△ABC≌△CDA得到：AC＝CA，故本选项不符合题意；


B、由△ABC≌△CDA得到：AB＝CD，推不出AB＝AD，故本选项符合题意；


C、由△ABC≌△CDA得到：∠ACB＝∠CAD，故本选项不符合题意；


D、由△ABC≌△CDA得到：∠B＝∠D，故本选项不符合题意；


故选：B．


3．解：∵∠BAD＝∠BCD＝90°，


∴△BAD和△BCD均为直角三角形．


∵，


∴△BAD≌BCD（HL）．


4．解：∵△EDB≌△EDC，


∴∠DEB＝∠DEC＝90°，


∵△ADB≌△EDB≌△EDC，


∴∠ABD＝∠DBC＝∠C，∠BAD＝∠DEB＝90°，


∴∠C＝30°，


故选：D．


5．解：∵PA＝PB，


∴∠A＝∠B，


在△AMK和△BKN中，


，


∴△AMK≌△BKN（SAS），


∴∠AMK＝∠BKN，


∵∠A+∠AMK＝∠MKN+∠BKN，


∴∠A＝∠MKN＝40°＝∠B，


∴∠P＝180°﹣∠A﹣∠B＝180°﹣40°﹣40°＝100°，


故选：A．


6．解：∵AB＝AC，


∴∠B＝∠C，


在△BDE和△CFD中


，


∴△BDE≌△CFD（SAS），


∴∠BED＝∠CDF，∠BDE＝∠CFD，


∴∠BED+∠BDE＝∠CDF+∠CFD，


∵∠BED+∠BDE+∠B＝∠CDF+∠CFD+∠EDF＝180°，


∴∠B＝∠EDF＝54°，


∴∠A＝180°﹣2×54°＝72°，


故选：B．


7．解：第一块和第二块只保留了原三角形的一个角和部分边，根据这两块中的任一块均不能配一块与原来完全一样的；


第三块不仅保留了原来三角形的两个角还保留了一边，则可以根据ASA来配一块一样的玻璃．


最省事的方法是应带③去，理由是：ASA．


故选：C．


8．解：在这个区域内修建一个集贸市场，要使集贸市场到三条公路的距离相等，


根据角平分线的性质，集贸市场应建在∠A、∠B、∠C的角平分线的交点处．


故选：C．


9．解：∵两根钢条AB，CD的中点O连在一起，


∴OA＝OB，OC＝OA，


∵∠AOC＝∠BOD，


∴△AOC≌△BOD．


∴AC＝BD，


用的是SAS的判定定理．


故选：A．


10．解：在Rt△OMP和Rt△ONP中，，


∴Rt△OMP≌Rt△ONP（HL），


∴∠MOP＝∠NOP，


∴OP是∠AOB的平分线．


故选：D．


11．解：∵BF＝CE，


∴BE＝CF．


①AE＝DF时，


在△ABE和△DCF中，，


∴△ABE≌△DCF（SSS）；故①正确；


②∵AE∥DF，


∴∠AEF＝∠DFC．


在△ABE和△DCF中，AB＝DC，BE＝CF，∠AEF＝∠DFC．


不能判定△ABE与△DCF全等，故②不正确；


③∵AB∥DC，


∴∠B＝∠C，


在△ABE和△DCF中，，


∴△ABE≌△DCF（SAS）；故③正确；


④在△ABE和△DCF中，AB＝DC，BE＝CF，∠A＝∠D．


不能判定△ABE与△DCF全等，故④不正确；


故选：A．


12．解：①∵BD为△ABC的角平分线，


∴∠ABD＝∠CBD，


在△ABD和△EBC中，，


∴△ABD≌△EBC（SAS），①正确；


②∵BD为△ABC的角平分线，BD＝BC，BE＝BA，


∴∠BCD＝∠BDC＝∠BAE＝∠BEA，


∵△ABD≌△EBC，


∴∠BCE＝∠BDA，AD＝EC，


∴∠BCE+∠BCD＝∠BDA+∠BDC＝180°，②正确；


③由②得：∠BDC＝∠BEA，


又∵∠ADE＝∠BDC，


∴∠ADE＝∠BEA，


∴AD＝AE，


∴AD＝AE＝EC，③正确；


④∵AD＝AE＝EC，AE+CE＞AD+CD，


∴AD＞CD，


∴AC≠2CD，故④错误，


故选：C．





二．填空题（共7小题）


13．解：∵∠A：∠ABC：∠ACB＝3：5：10，


∴∠ACB＝180°×＝100°，


∵△EDC≌△ABC，


∴∠ECD＝∠ACB＝100°，


∴∠ECA＝180°﹣∠ECD＝180°﹣100°＝80°，


∠BCE＝∠ACB﹣∠ECA＝100°﹣80°＝20°，


故答案为：20°


14．解：∵△ABC≌△DEF，


∴∠E＝∠B＝120°，


∵∠F＝35°，


∴∠D＝180°﹣∠E﹣∠F＝25°，


故答案为25．


15．解：添加AC＝BC，


∵△ABC的两条高AD，BE，


∴∠ADC＝∠BEC＝90°，


在△ADC和△BEC中，


∴△ADC≌△BEC（AAS），


故答案为：AC＝BC．


16．解：作OE⊥AB于E，OF⊥BC于F，OH⊥AC于H，


∵△ABC的三条角平分线交于点O，OE⊥AB，OF⊥BC，OH⊥AC，


∴OF＝OH＝OE＝3，


∴△ABC的面积＝×（AB+BC+AC）×3＝27，


故答案为：27．





17．解：∵∠ACB＝90°，


∴∠BCE+∠ACD＝90°，


又∵BE⊥CE，AD⊥CE，


∴∠E＝∠ADC＝90°，


∴∠BCE+∠CBE＝90°，


∴∠CBE＝∠ACD，


在△CBE和△ACD中，，


∴△CBE≌△ACD（AAS），


∴AC＝BC＝13，CD＝BE＝5，


∴CE＝，


∴DE＝CE﹣CD＝12﹣5＝7，


故答案为：7；


18．解：在△ADC和△ABC中，


，


∴△ADC≌△ABC（SSS）．


∴∠DAC＝∠BAC，


即∠QAE＝∠PAE．


故答案为：SSS．


19．解：∵在△ABC和△DBE中，


∴△ABC≌△DBE（SAS），


∴∠3＝∠ACB，


∵∠ACB+∠1＝90°，


∴∠1+∠3＝90°，


∴∠1+∠2+∠3＝90°+45°＝135°，


故答案为：135°．





三．解答题（共5小题）


20．（1）证明：在△BDA和△CAD中





∴△BDA≌△CAD（SSS）


∴∠ABD＝∠DCA，


在△AOB和△DOC





∴△AOB≌△DOC（AAS）；


（2）图中与∠ACB相等的角是∠ABD、∠ADB、∠DAC、∠DBC、∠DCA，


理由：∵AD∥BC，


∴∠DAC＝∠ACB，∠ADB＝∠DBC，


∵AB＝AD，AD＝DC，


∴∠ABD＝∠ADB，∠DAC＝∠DCA，


∴∠ACB＝∠DAC＝∠DCA，


由（1）知，△AOB≌△DOC，


∴OA＝OD，


∴∠DAC＝∠ADB，


∴∠ACB＝∠ABD＝∠ADB＝∠DAC＝∠DBC＝∠DCA，


即图中与∠ACB相等的角是∠ABD、∠ADB、∠DAC、∠DBC、∠DCA．


21．（1）证明：∵CE＝BF，


∴CE+EF＝BF+EF，


∴BE＝CF，


在△ABE和△DCF中，，


∴△ABE≌△DCF（SSS），


∴∠B＝∠C；


（2）解：由（1）得：△ABE≌△DCF，


∴∠AEB＝∠DFC＝30°，


∴∠BAE＝180°﹣∠B﹣∠AEB＝180°﹣40°﹣30°＝110°，


∵AF平分∠BAE，


∴∠BAF＝∠BAE＝×110°＝55°．


22．解：（1）∵AB＝AC，


∴∠C＝∠B＝36°，


∵∠ADE＝36°，∠BDA＝128°，


∵∠EDC＝180°﹣∠ADB﹣∠ADE＝16°，


∴∠AED＝∠EDC+∠C＝16°+36°＝52°，


故答案为：16°；52°；


（2）当DC＝2时，△ABD≌△DCE，


理由：∵AB＝2，DC＝2，


∴AB＝DC，


∵∠C＝36°，


∴∠DEC+∠EDC＝144°，


∵∠ADE＝36°，


∴∠ADB+∠EDC＝144°，


∴∠ADB＝∠DEC，


在△ABD和△DCE中，


，


∴△ABD≌△DCE（AAS）；


（3）当∠BDA的度数为108°或72°时，△ADE的形状是等腰三角形，


①当DA＝DE时，∠DAE＝∠DEA＝72°，


∴∠BDA＝∠DAE+∠C＝72°+36°＝108°；


②当AD＝AE时，∠AED＝∠ADE＝36°，


∴∠DAE＝108°，


此时，点D与点B重合，不合题意；


③当EA＝ED时，∠EAD＝∠ADE＝36°，


∴∠BDA＝∠EAD+∠C＝36°+36°＝72°；


综上所述，当∠BDA的度数为108°或72°时，△ADE的形状是等腰三角形．


23．（1）证明：∵DB是高，


∴∠ABE＝∠DBC＝90°．


在△ABE和△DBC中，，


∴△ABE≌△DBC．


（2）解：BM＝BN，MB⊥BN．


证明如下：


∵△ABE≌△DBC，


∴∠BAM＝∠BDN．


在△ABM 和△DBN 中，


∴△ABM≌△DBN（SAS）．


∴BM＝BN，∠ABM＝∠DBN．


∴∠DBN+∠DBM＝∠ABM+∠DBM＝∠ABD＝90°．


∴MB⊥BN．


24．（1）解：如图1，延长AC交BN于点F，


∵AM∥BN，


∴∠DAF＝∠AFB，


在△ADC和△FEC中，，


∴△ADC≌△FEC（AAS），


∴AC＝FC，


∵AC＝BC，


∴BC＝AC＝FC＝AF，


∴△ABF是直角三角形，


∴∠ABE＝90°；


（2）证明：如图2，在EB上截取EH＝EC，连CH，


∵AC＝BC，∠ABC＝60°，


∴△ABC为等边三角形，


∵∠DEB＝60°，


∴△CHE是等边三角形，


∴∠CHE＝60°，∠HCE＝60°，


∴∠BHC＝120°，


∵AM∥BN，


∴∠ADC+∠BEC＝180°，


∴∠ADC＝120°，


∴∠DAC+∠DCA＝60°，


又∵∠DCA+∠ACB+∠BCH+∠HCE＝180°，


∴∠DCA+∠BCH＝60°，


∴∠DAC＝∠BCH，


在△DAC与△HCB中，，


∴△DAC≌△HCB（AAS），


∴AD＝CH，DC＝BH，


又∵CH＝CE＝HE，


∴BE＝BH+HE＝DC+AD，


即AD+DC＝BE．