2020版《微点教程》高考人教A版理科数学一轮复习文档：第四章第一节　平面向量的概念及其线性运算 学案

第四章  平面向量、数系的扩充与复数的引入

第一节　平面向量的概念及其线性运算

2019考纲考题考情

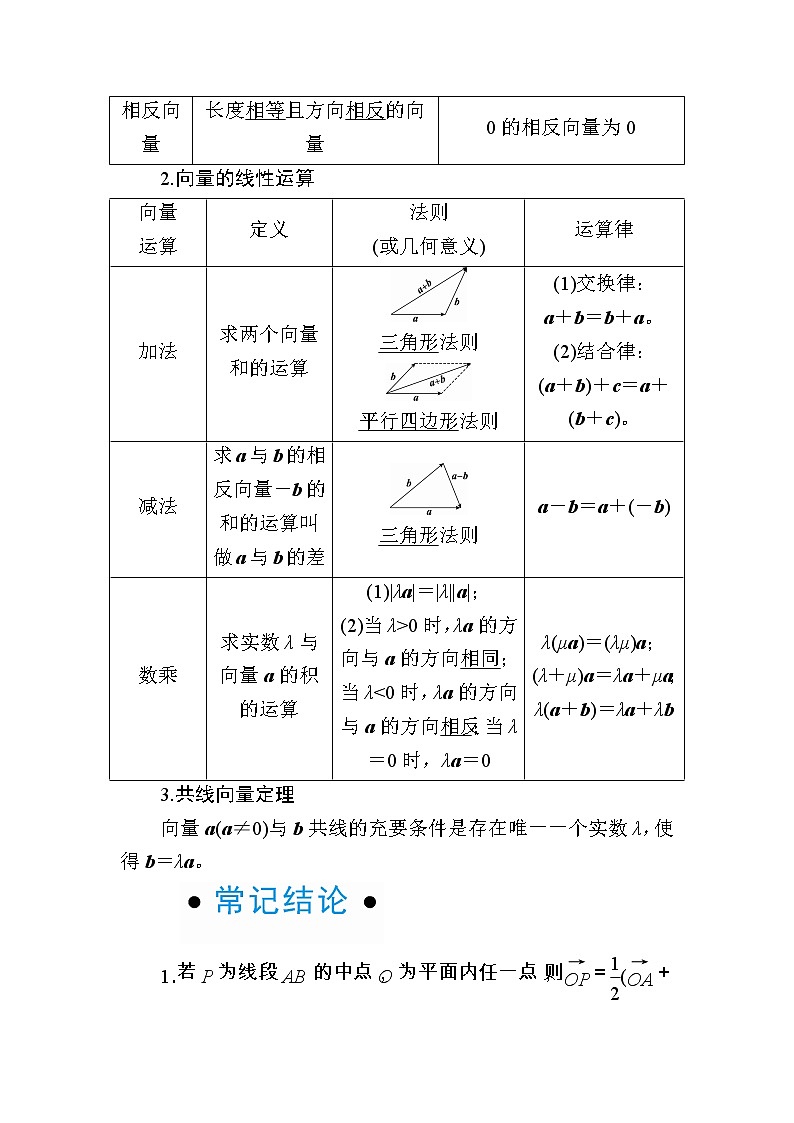
1．向量的有关概念

2.向量的线性运算

3.共线向量定理

向量a(a≠0)与b共线的充要条件是存在唯一一个实数λ，使得b＝λa。

1．若P为线段AB的中点，O为平面内任一点，则＝(＋)。

2.＝λ＋μ(λ，μ为实数)，若点A，B，C共线，则λ＋μ＝1。

3．解决向量的概念问题要注意两点：一是不仅要考虑向量的大小，更重要的是要考虑向量的方向；二是考虑零向量是否也满足条件。要特别注意零向量的特殊性。

一、走进教材

1．(必修4P86例4改编)已知▱ABCD的对角线AC和BD相交于点O，且＝a，＝b，则＝________，＝________。(用a，b表示)

解析　如图，＝＝－＝b－a，＝－＝－－＝－a－b。

答案　b－a　－a－b

2．(必修4P108B组T5)在平行四边形ABCD中，若|＋|＝|－|，则四边形ABCD的形状为 ________。

解析　如图，因为＋＝，－＝，所以||＝||。由对角线长相等的平行四边形是矩形可知，四边形ABCD是矩形。

答案　矩形

二、走近高考

3．(2018·全国卷Ⅰ)在△ABC中，AD为BC边上的中线，E为AD的中点，则＝(　　)

A．－ B．－

C.＋ D.＋

解析　如图所示，＝＋＝＋＝×(＋)＋(－)＝－，故选A。

解析：＝－＝－＝－××(＋)＝－，故选A。

答案　A

4．(2015·全国卷Ⅱ)设向量a，b不平行，向量λa＋b与a＋2b平行，则实数λ＝________。

解析　因为λa＋b与a＋2b平行，所以存在唯一实数t，使得λa＋b＝t(a＋2b)，所以解得λ＝t＝。

答案　

三、走出误区

微提醒：①对向量共线定理认识不准确；②向量线性运算不熟致错；③向量三角不等式认识不清致错。

5．对于非零向量a，b，“a＋b＝0”是“a∥b”的(　　)

A．充分不必要条件

B．必要不充分条件

C．充要条件

D．既不充分也不必要条件

解析　若a＋b＝0，则a＝－b，所以a∥b。若a∥b，则a＋b＝0不一定成立。故前者是后者的充分不必要条件。

答案　A

6．如图，已知＝，用，表示，则等于(　　)

A．－   B．＋

C．－＋   D．－－

解析　＝＋＝＋＝＋(－)＝－＋。故选C。

答案　C

7．已知向量a，b，若|a|＝2，|b|＝4，则|a－b|的取值范围为________。

解析　当a与b方向相同时，|a－b|＝2，当a与b方向相反时，|a－b|＝6，当a与b不共线时，2<|a－b|<6，所以|a－b|的取值范围为[2,6]。此题易忽视a与b方向相同和a与b方向相反两种情况。

答案　[2,6]

,学生用书P082

　　【例1】　给出下列四个命题：

①若|a|＝|b|，则a＝b；

②若A，B，C，D是不共线的四点，则“＝”是“四边形ABCD为平行四边形”的充要条件；

③若a＝b，b＝c，则a＝c；

④a＝b的充要条件是|a|＝|b|且a∥b。

其中正确命题的序号是(　　)

A．②③ B．①②

C．③④ D．②④

解析　①不正确。两个向量的长度相等，但它们的方向不一定相同。②正确。因为＝，所以||＝||且∥，又A，B，C，D是不共线的四点，所以四边形ABCD为平行四边形；反之，若四边形ABCD为平行四边形，则||＝||，∥且，方向相同，因此＝。③正确。因为a＝b，所以a，b的长度相等且方向相同，又b＝c，所以b，c的长度相等且方向相同，所以a，c的长度相等且方向相同，故a＝c。④不正确。当a∥b且方向相反时，即使|a|＝|b|，也不能得到a＝b，故|a|＝|b|且a∥b不是a＝b的充要条件，而是必要不充分条件。综上所述，正确命题的序号是②③。

答案　A

1．相等向量具有传递性，非零向量的平行也具有传递性。

2．共线向量即为平行向量，它们均与起点无关。

3．向量可以平移，平移后的向量与原向量是相等向量。解题时，不要把它与函数图象的移动混为一谈。

4．非零向量a与的关系：是与a同方向的单位向量。

【变式训练】　(1)设a，b都是非零向量，下列四个条件中，一定能使＋＝0成立的是(　　)

A．a＝2b B．a∥b

C．a＝－b D．a⊥b

(2)给出下列说法：

①非零向量a与b同向是a＝b的必要不充分条件；

②若与共线，则A，B，C三点在同一条直线上；

③a与b是非零向量，若a与b同向，则a与－b反向；

④设λ，μ为实数，若λa＝μb，则a与b共线。

其中错误说法的序号是________。

解析　(1)由＋＝0得＝－≠0，即a＝－·|a|≠0，则a与b共线且方向相反，因此当向量a与向量b共线且方向相反时，能使＋＝0成立。对照各个选项可知，选项A中a与b的方向相同；选项B中a与b共线，方向相同或相反；选项C中a与b的方向相反；选项D中a与b互相垂直。故选C。

(2)根据向量的有关概念可知①②③正确，对于④，当λ＝μ＝0时，a与b不一定共线，故④错误。

答案　(1)C　(2)④

　　【例2】　(1)已知O，A，B是平面上的三个点，直线AB上有一点C，满足2＋＝0，则＝(　　)

A．2－ B．－＋2

C.－ D．－＋

(2)(2019·福建高三质检)庄严美丽的国旗和国徽上的五角星是革命和光明的象征。正五角星是一个非常优美的几何图形，且与黄金分割有着密切的联系：在如图所示的正五角星中，以A，B，C，D，E为顶点的多边形为正五边形，且＝。下列关系中正确的是(　　)

A．－＝ B．＋＝

C.－＝ D.＋＝

解析　(1)因为2＋＝0，所以A为BC的中点，所以2＝＋，故＝2－。

(2)由题意得，－＝－＝＝＝，所以A正确；＋＝＋＝＝，所以B错误；－＝－＝＝，所以C错误；＋＝＋，＝＝－，若＋＝，则＝0，不合题意，所以D错误。故选A。

答案　(1)A　(2)A

向量线性运算的应用技巧

1．灵活运用向量加、减法中的平行四边形法则和三角形法则。

2．充分利用平面几何知识，发掘直线的平行关系和线段的比例关系。必要时，可添加辅助线。

【变式训练】　(1)已知三角形ABC是等边三角形，D为AB的中点，点E满足2＋＝0，则＝(　　)

A．－ B．＋

C.－ D.＋

(2)如图所示，已知AB是圆O的直径，点C，D是半圆弧的两个三等分点，＝a，＝b，则＝(　　)

A．a－b B．a－b

C．a＋b D.a＋b

解析　(1)由2＋＝0知＝，＝，所以＝＋＝＋＝＋(＋)＝＋＝－。

(2)连接CD，由点C，D是半圆弧的三等分点，得CD∥AB，且＝＝a，所以＝＋＝b＋a。

答案　(1)A　(2)D

考点三   共线定理及应用微点小专题

方向1：共线定理

【例3】　已知e1，e2是两个不共线的向量，若a＝2e1－e2与b＝e1＋λe2共线，则λ＝(　　)

A．－   B．－2

C.   D．2

解析　若向量a与b共线，则存在实数μ使得2e1－e2＝μ(e1＋λe2)，则有解得λ＝－。故选A。

答案　A

两个向量共线是指两个向量的方向相同或相反，因此共线包含两种情况：同向共线或反向共线。一般地，若a＝λb(b≠0)，则a与b共线：

(1)当λ>0时，a与b同向；

(2)当λ<0时，a与b反向。

方向2：共线定理的应用

【例4】　如图，一直线EF与平行四边形ABCD的两边AB，AD分别交于E，F两点，且交对角线AC于点K，其中，＝，＝，＝λ，则λ的值为(　　)

A． B．

C. D.

解析　因为＝，＝，所以＝，＝2。由向量加法的平行四边形法则可知，＝＋，所以＝λ＝λ(＋)＝λ＝λ＋2λ，由E，F，K三点共线，可得λ＋2λ＝1，可得λ＝，故选A。

答案　A

1．共线向量定理是解决三点共线问题的有利工具

解题过程中常用到结论：“P，A，B三点共线”等价于“对直线AB外任意一点O，总存在非零实数λ，使＝λ＋(1－λ)成立”。

2．含参共线问题的解法

解决含有参数的共线问题时，经常要用到平面几何的性质，构造含有参数的方程或方程组，解方程或方程组得到参数的值。

【题点对应练】　

1．(方向1)(2018·郑州模拟)设e1与e2是两个不共线向量，＝3e1＋2e2，＝ke1＋e2，＝3e1－2ke2，若A，B，D三点共线，则k的值为________。

解析　由题意，A，B，D三点共线，故必存在一个实数λ，使得＝λ。又＝3e1＋2e2，＝ke1＋e2，＝3e1－2ke2，所以＝－＝3e1－2ke2－(ke1＋e2)＝(3－k)e1－(2k＋1)e2，所以3e1＋2e2＝λ(3－k)e1－λ(2k＋1)e2，又e1与e2不共线，所以解得k＝－。

答案　－

2．(方向2)(2019·辽宁五校协作体模拟)在△ABC中，点P满足＝2，过点P的直线与AB，AC所在直线分别交于点M，N，若＝m，＝n(m>0，n>0)，则m＋2n的最小值为(　　)

A．3　　　　 B．4 

C.　　　　 D.

解析　因为＝2，所以－＝2(－)，所以＝＋，又因为＝m，＝n，所以＝＋。因为M，P，N三点共线，所以＋＝1，所以m＋2n＝(m＋2n)＝＋＋≥＋×2 ＝＋＝3，当且仅当即m＝n＝1时等号成立。所以m＋2n的最小值为3。故选A。

答案　A

共线定理的推广

共线定理：已知，为平面内两个不共线的向量，设＝x＋y，则A，B，C三点共线的充要条件为x＋y＝1。

推广形式：如图所示，直线DE∥AB，C为直线DE上任一点，设＝x＋y(x，y∈R)。

当直线DE不过点P时，直线PC与直线AB的交点记为F，因为点F在直线AB上，所以由三点共线结论可知，若＝λ＋μ(λ，μ∈R)，则λ＋μ＝1。由△PAB与△PED相似，知必存在一个常数m∈R，使得＝m，则＝m＝mλ＋mμ。

又＝x＋y(x，y∈R)，

所以x＋y＝mλ＋mμ＝m。

以上过程可逆。

因此得到结论：＝x＋y，

则x＋y＝m(定值)，反之亦成立。

【典例1】　如图，在正六边形ABCDEF中，P是△CDE内(包括边界)的动点，设＝α＋β(α，β∈R)，则α＋β的取值范围是________。

【解析】　当P在△CDE内时，直线EC是最近的平行线，过D点的平行线是最远的，所以α＋β∈＝[3,4]。

【答案】　[3,4]

【典例2】　如图所示，A，B，C是圆O上的三点，线段CO的延长线与BA的延长线交于圆O外的一点D，若＝m＋n，则m＋n的取值范围是________。

【解析】　由点D是圆O外的一点，可设＝λ(λ>1)，则＝＋＝＋λ＝λ＋(1－λ)。因为C、O、D三点共线，令＝－μ(μ>1)。所以＝－－(λ>1，μ>1)。因为＝m＋n，所以m＝－，n＝－，所以m＋n＝－－＝－∈(－1,0)。

【答案】　(－1,0)

【变式训练】　如图，在扇形OAB中，∠AOB＝，C为弧AB上的动点，若＝x＋y，则x＋3y的取值范围是________。

解析　＝x＋3y，如图，作＝，则考虑以向量，为基底。显然，当C在A点时，经过m＝1的平行线，当C在B点时，经过m＝3的平行线，这两条线分别是最近与最远的平行线，所以x＋3y的取值范围是[1,3]。

答案　[1,3]