2020年高考物理一轮复习文档：第3章牛顿运动定律第14讲 学案

第14讲　牛顿运动定律的综合应用(2)
考点一　多过程问题

1．多过程问题就是物体的运动过程由许多“子过程”组成，各“子过程”有关键物理量前后相联系，往往叫做过程“衔接量”。
2．对各个“子过程”进行受力分析和运动分析，一般要画出过程示意图，关键是找出过程“衔接量”进行分析研究。
3．分析各“子过程”列关系式时，一般前后过程中都有“衔接量”，如速度、时间等。
4．联立方程组，分析求解，对结果进行必要的验证或讨论。

(2015·全国卷Ⅱ)下暴雨时，有时会发生山体滑坡或泥石流等地质灾害。某地有一倾角为θ＝37°的山坡C，上面有一质量为m的石板B，其上下表面与斜坡平行；B上有一碎石堆A(含有大量泥土)，A和B均处于静止状态，如图所示。假设某次暴雨中，A浸透雨水后总质量也为m(可视为质量不变的滑块)，在极短时间内，A、B间的动摩擦因数μ1减小为，B、C间的动摩擦因数μ2减小为0.5，A、B开始运动，此时刻为计时起点；在第2 s末，B的上表面突然变为光滑，μ2保持不变。已知A开始运动时，A离B下边缘的距离l＝27 m，C足够长。设最大静摩擦力等于滑动摩擦力。取重力加速度大小g＝10 m/s2。求：

(1)在0～2 s时间内A和B加速度的大小；
(2)A在B上总的运动时间。
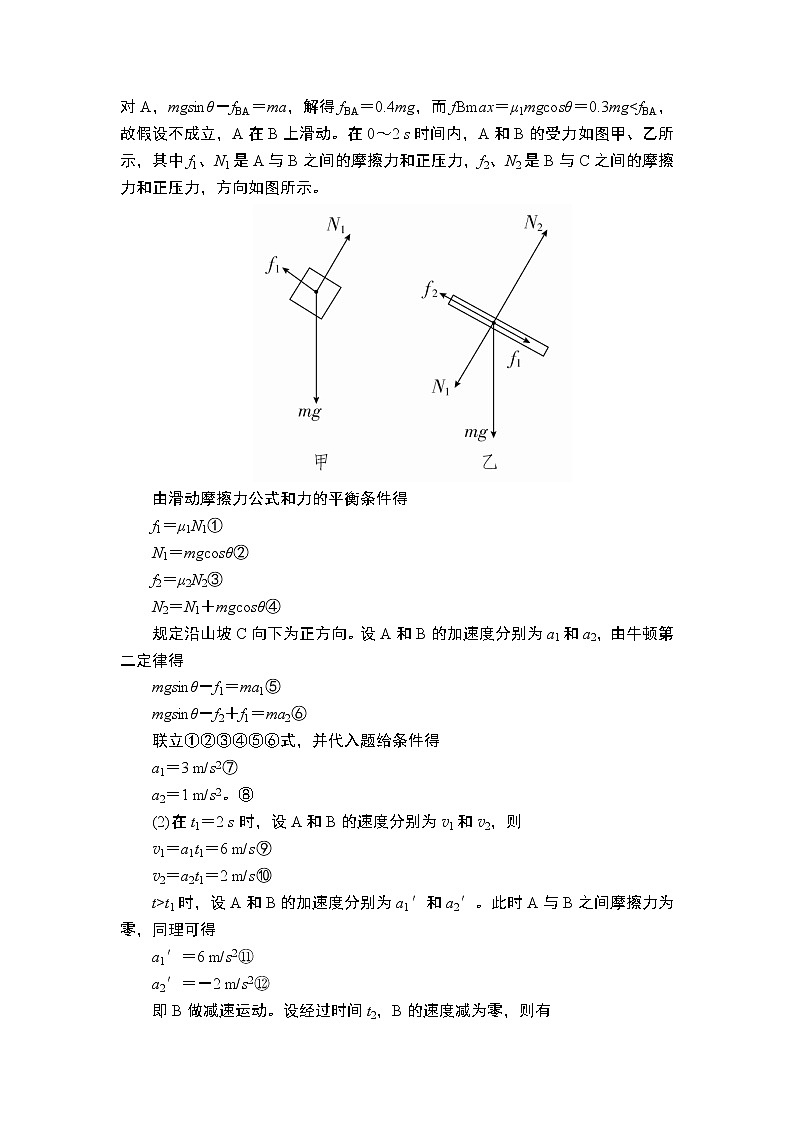
解析　(1)假设0～2 s内A、B相对静止，则2mgsinθ－μ2·2mgcosθ＝2ma，对A，mgsinθ－fBA＝ma，解得fBA＝0.4mg，而fBmax＝μ1mgcosθ＝0.3mg
由滑动摩擦力公式和力的平衡条件得
f1＝μ1N1①
N1＝mgcosθ②
f2＝μ2N2③
N2＝N1＋mgcosθ④
规定沿山坡C向下为正方向。设A和B的加速度分别为a1和a2，由牛顿第二定律得
mgsinθ－f1＝ma1⑤
mgsinθ－f2＋f1＝ma2⑥
联立①②③④⑤⑥式，并代入题给条件得
a1＝3 m/s2⑦
a2＝1 m/s2。⑧
(2)在t1＝2 s时，设A和B的速度分别为v1和v2，则
v1＝a1t1＝6 m/s⑨
v2＝a2t1＝2 m/s⑩
t>t1时，设A和B的加速度分别为a1′和a2′。此时A与B之间摩擦力为零，同理可得
a1′＝6 m/s2⑪
a2′＝－2 m/s2⑫
即B做减速运动。设经过时间t2，B的速度减为零，则有
v2＋a2′t2＝0⑬
联立⑩⑫⑬式得t2＝1 s⑭
在t1＋t2时间内，A相对于B运动的距离为
s＝－＝12 m<27 m⑮
此后B静止不动，A继续在B上滑动。设再经过时间t3 A离开B，则有
l－s＝(v1＋a1′t2)t3＋a1′t⑯
可得t3＝1 s(另一解不合题意，舍去)⑰
设A在B上总的运动时间为t总，有
t总＝t1＋t2＋t3＝4 s。
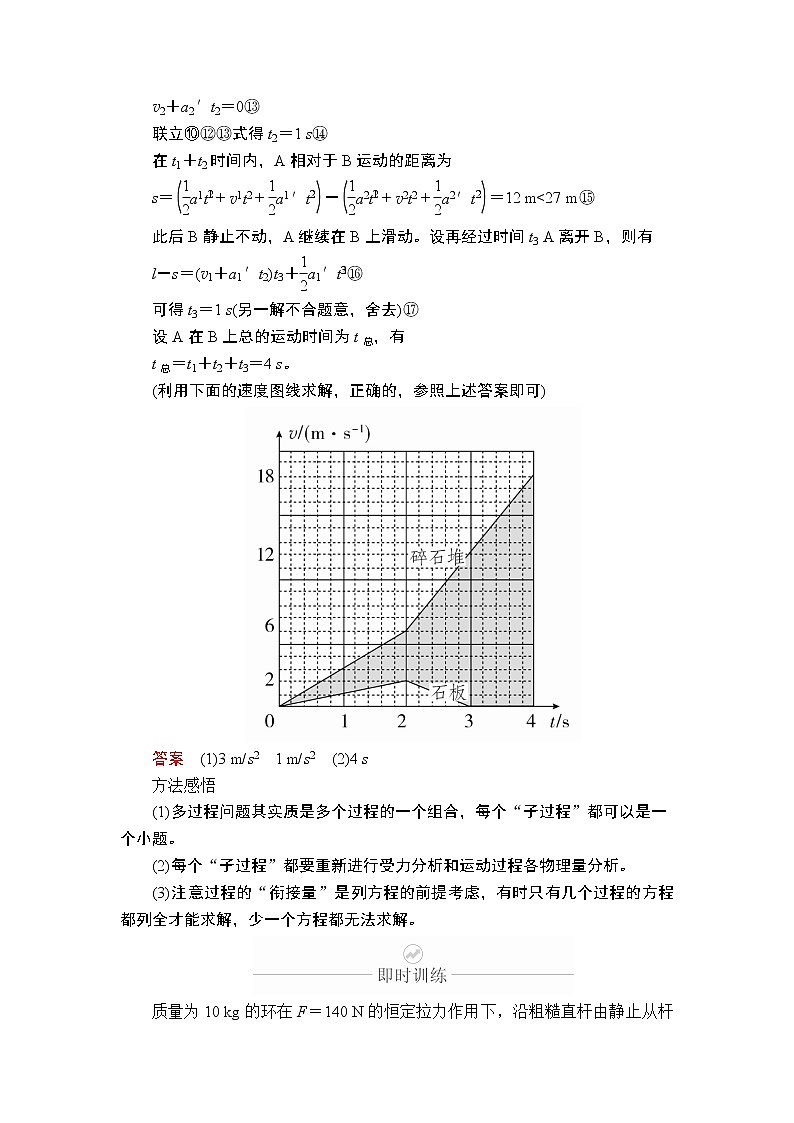
(利用下面的速度图线求解，正确的，参照上述答案即可)

答案　(1)3 m/s2　1 m/s2　(2)4 s
方法感悟
(1)多过程问题其实质是多个过程的一个组合，每个“子过程”都可以是一个小题。
(2)每个“子过程”都要重新进行受力分析和运动过程各物理量分析。
(3)注意过程的“衔接量”是列方程的前提考虑，有时只有几个过程的方程都列全才能求解，少一个方程都无法求解。

质量为10 kg的环在F＝140 N的恒定拉力作用下，沿粗糙直杆由静止从杆的底端开始运动，环与杆之间的动摩擦因数μ＝0.5，杆与水平地面的夹角为θ＝37°，拉力F与杆的夹角θ＝37°，力F作用一段时间后撤去，环在杆上继续上滑了0.5 s后，速度减为零，g取10 m/s2，sin37°＝0.6，cos37°＝0.8，杆足够长。求：

(1)拉力F作用的时间；
(2)环运动到杆底端时的速度大小。
答案　(1)1 s　(2) m/s
解析　(1)撤去拉力F后，由牛顿第二定律有
mgsinθ＋μmgcosθ＝ma2
又0＝v1－a2t2
联立解得v1＝5 m/s。
撤去拉力F前(注意杆对环的弹力的方向)，有
Fcosθ－mgsinθ－μ(Fsinθ－mgcosθ)＝ma1
而v1＝a1t1
联立解得t1＝1 s。
(2)环速度为零后反向做匀加速直线运动，
由牛顿第二定律得mgsinθ－μmgcosθ＝ma3
又s＝(t1＋t2)，而v2＝2a3s
联立解得v＝ m/s。
考点二　临界状态和极值问题

1．在临界状态，系统的一些物理量达到极值。在临界点的两侧，物体的受力情况、运动状态一般要发生改变，能否用变化的观点正确分析其运动规律是求解这类题目的关键，而临界点的确定是基础。确定临界点一般用极端分析法，即把问题(物理过程)推到极端，分析在极端情况下可能出现的状态和满足的条件，应用牛顿第二定律列出极端情况下的方程求解。
2．临界或极值条件的物理语言
(1)有些题目中有“刚好”“恰好”“正好”等字眼，明显表明题述的过程存在着临界点。
(2)若题目中有“取值范围”“多长时间”“多大距离”等词语，表明题述的过程存在着“起止点”，而这些起止点往往就对应临界状态。
(3)若题目中有“最大”“最小”“至多”“至少”等字眼，表明题述的过程存在着极值，这个极值点往往是临界点。
(4)若题目要求“最终加速度”“稳定速度”等，即是求收尾加速度或收尾速度。

日本大地震以及随后的海啸给日本造成了巨大的损失。灾后某中学的部分学生组成了一个课题小组，对海啸的威力进行了模拟研究，他们设计了如下的模型：如图甲所示，在水平地面上放置一个质量为m＝4 kg的物体，让其在随位移均匀减小的水平推力作用下运动，推力F随位移x变化的图象如图乙所示。已知物体与地面之间的动摩擦因数为μ＝0.5，g＝10 m/s2。求：

(1)运动过程中物体的最大加速度为多少？
(2)距出发点多远时物体的速度达到最大？
解析　(1)由牛顿第二定律得F－μmg＝ma，当推力F＝100 N时，物体所受合力最大，加速度最大，代入数据解得a＝－μg＝20 m/s2。
(2)由图象求出，推力F随位移x变化的函数关系为：F＝100－25x，当物体加速度为零时，速度最大，则F＝μmg时，a＝0，故代入数据解得x＝3.2 m。
答案　(1)20 m/s2　(2)3.2 m
方法感悟
常见的几种临界条件
(1)接触与脱离的临界条件FN＝0。
(2)相对滑动的临界条件一般是加速度不同。
(3)绳子断裂或松弛的临界条件是绳子达到最大张力或绳子拉力恰好为零。
(4)加速度最大或速度最大的临界条件：合外力最大时具有最大加速度，合外力最小时具有最小加速度，合外力一直减小到零时具有最小速度或最大速度。

(多选)如图甲所示，平行于光滑斜面的轻弹簧劲度系数为k，一端固定在倾角为θ的斜面底端，另一端与物块A连接，两物块A、B质量均为m，初始时均静止。现用平行于斜面向上的力F拉动物块B，使B做加速度为a的匀加速运动，A、B两物块在开始一段时间内的v­t关系分别对应图乙中A、B图线，t1时刻A、B的图线分离，则下列说法中正确的是(　　)

A．t1时刻，弹簧形变量为
B．t2时刻，弹簧形变量为
C．t1时刻，A、B刚分离时的速度为
D．从开始到t2时刻，拉力F先逐渐增大后不变
答案　BD
解析　由图读出，t1时刻A、B开始分离，对A根据牛顿第二定律：kx1－mgsinθ＝ma，则x1＝，故A错误；由图知，t2时刻A的加速度为零，速度最大，根据牛顿第二定律和胡克定律：mgsinθ＝kx2，得x2＝，故B正确；由图读出，t1时刻A、B开始分离，对A根据牛顿第二定律：kx1－mgsinθ＝ma，开始时有2mgsinθ＝kx0，又x0－x1＝at，速度v＝at1＝ ，故C错误；从开始到t1时刻，对A、B整体，根据牛顿第二定律得F＋kx－2mgsinθ＝2ma，得F＝2mgsinθ＋2ma－kx，x减小，F增大，t1时刻到t2时刻，对B，由牛顿第二定律得F－mgsinθ＝ma，得F＝mgsinθ＋ma，可知F不变，故D正确。
课后作业
[巩固强化练]
1. (多选)如图所示，A、B两物块的质量分别为2m和m，静止叠放在水平地面上。A、B间的动摩擦因数为μ，B与地面间的动摩擦因数为μ，最大静摩擦力等于滑动摩擦力，重力加速度为g。现对A施加一水平拉力F，则(　　)

A．当F<2μmg时，A、B都相对地面静止
B．当F＝μmg时，A的加速度为μg
C．当F>3μmg时，A相对B滑动
D．无论F为何值，B的加速度不会超过μg
答案　BCD
解析　当A、B整体将要相对地面滑动时有F＝μ(2m＋m)g＝μmg，即当03μmg时，A相对B向右做加速运动，B相对地面也向右加速，A错误，C正确。当F＝μmg时，A与B共同的加速度a＝＝μg，B正确。F>3μmg时，取物块B为研究对象，物块B的加速度最大为a2＝＝μg，D正确。
2. 如图所示，在倾角为30°的光滑斜面上放置质量分别为m和2m的A、B、C、D四个木块，其中A、C两个质量为m的木块间用一不可伸长的轻绳相连，木块间的最大静摩擦力是fm。现用平行于斜面的拉力F拉其中质量为2m的B木块，使四个木块以同一加速度沿斜面向下运动，则拉力F的最大值是(　　)

A.fm B.fm C.fm D．fm
答案　C
解析　设整体加速度为a，对D木块受力分析，
有Ff1＋2mgsin30°＝2ma①
对A、C、D三个木块组成的整体受力分析，
有Ff2＋4mgsin30°＝4ma②
由于木块间的最大静摩擦力大小都为fm，且Ff2>Ff1，所以整体加速度增大时，A、B间的静摩擦力先达到最大静摩擦力，取
Ff2＝fm③
再对整体受力分析，有F＋6mgsin30°＝6ma④
由②③④得F＝fm，C正确。
3．将一轻质弹簧竖直立在水平面上，当在其上端放上托盘Q时，平衡时弹簧缩短了3 cm；当将一个物块P轻轻放在托盘中，待系统平衡后，弹簧又缩短了2 cm；如果此时在P上施加一个竖直向下的力F，待系统再次平衡后，弹簧又缩短了2 cm，如图所示。若在此时突然撤去力F，则(弹簧始终处于弹性限度内，重力加速度为g) (　　)

A．刚撤去力F瞬间，物块P的加速度大小为0.4g
B．刚撤去力F瞬间，物块P的加速度大小为0.8g
C．撤去力F后，物块P、Q共同向上运动5 cm后分离
D．撤去力F后，物块P、Q共同向上运动7 cm后分离
答案　A
解析　当在其上端放上托盘Q时，平衡时弹簧缩短了3 cm，则m1g＝kx1，当将一个物块P轻轻放在托盘中，待系统平衡后，弹簧又缩短了2 cm，此时m1g＋m2g＝k(x1＋x2)，撤去F后，k(x1＋x2＋x3)－(m1g＋m2g)＝(m1＋m2)a，联立代入数据得a＝0.4g，故A正确，B错误；由于在物块P上施加力F之前，弹簧已经压缩了5 cm，撤去力后，P与Q和弹簧组成的系统是一个弹簧振子系统，其振幅大小等于再次的压缩量，即2 cm，所以PQ向上运动的最大位移是4 cm，PQ不可能会分离，故C、D错误。
4．如图所示，在光滑水平面上，放置着A、B两个物体。A、B紧靠在一起，其质量分别为mA＝3 kg，mB＝6 kg，推力FA作用于A上，拉力FB作用于B上，FA、FB大小均随时间而变化，其规律为FA＝(12－2t) N，FB＝(6＋2t) N。问从t＝0开始，到A、B相互脱离为止，A、B的共同位移是多少？

答案　9 m
解析　FA、FB的大小虽随时间而变化，但F合＝FA＋FB＝18 N不变，故开始一段时间内A、B共同做匀加速运动，A、B分离前，对整体有：FA＋FB＝(mA＋mB)a ①
设A、B间的弹力为FAB，
对B有：FB＋FAB＝mBa②
由于加速度a恒定，则随着t的增大，FB增大，弹力FAB逐渐减小，当A、B恰好分离时，A、B间的弹力为零，即FAB＝0③
将FA＝(12－2t) N，FB＝(6＋2t) N代入①式
得：a＝2 m/s2。
联立②③式得：t＝3 s。
A、B相互脱离前共同位移为：x＝at2，
代入数值得：x＝9 m。
5．静止在水平面上的A、B两个物体通过一根拉直的轻绳相连，如图所示，轻绳长L＝1 m，承受的最大拉力为8 N，A的质量m1＝2 kg，B的质量m2＝8 kg，A、B与水平面间的动摩擦因数μ＝0.2，现用一逐渐增大的水平力作用在B上，使A、B向右运动，当F增大到某一值时，轻绳刚好被拉断(取g＝10 m/s2)。

(1)求绳刚被拉断时F的大小；
(2)若绳刚被拉断时，A、B的速度为2 m/s，保持此时的F大小不变，当A的速度恰好减小为0时，A、B间的距离为多少？
答案　(1)40 N (2)3.5 m
解析　(1)设绳刚要被拉断时产生的拉力为T，根据牛顿第二定律，对A物体有T－μm1g＝m1a
代入数值得a＝2 m/s2。
对A、B整体有F－μ(m1＋m2)g＝(m1＋m2)a
代入数值得F＝40 N。
(2)设绳断后，A的加速度大小为a1，B的加速度大小为a2，则
a1＝＝2 m/s2
a2＝＝3 m/s2
A停下来的时间为t＝＝1 s
A的位移为x1＝＝1 m
B的位移为x2＝vt＋a2t2＝3.5 m
A刚静止时，A、B间距离为Δx＝x2＋L－x1＝3.5 m。

6．如图所示，一条轻绳上端系在车的左上角的A点，另一条轻绳一端系在车左端B点，B点在A点的正下方，A、B距离为b，两条轻绳另一端在C点相结并系一个质量为m的小球，轻绳AC长度为b，轻绳BC长度为b。两条轻绳能够承受的最大拉力均为2mg。
(1)轻绳BC刚好被拉直时，车的加速度是多大？(要求画出受力图)
(2)在不拉断轻绳的前提下，求车向左运动的最大加速度是多大？(要求画出受力图)
答案　(1)g 见解析图甲 (2)3g 见解析图乙
解析　(1)轻绳BC刚好被拉直时，小球受力如图甲所示。因为AB＝BC＝b，AC＝b，故轻绳BC与AB垂直，θ＝45°。
由牛顿第二定律，得mgtanθ＝ma
可得a＝g。

(2)小车向左的加速度增大，BC绳方向不变，所以AC轻绳拉力不变，BC轻绳拉力变大，BC轻绳拉力最大时．小车向左的加速度最大，小球受力如图乙所示。
由牛顿第二定律，得FTm＋mgtanθ＝mam
因FTm＝2mg，所以最大加速度为am＝3g。
[真题模拟练]

7. (2018·河北唐山调研)(多选)如图所示，将小砝码放在桌面上的薄纸板上，若砝码和纸板的质量分别为M和m，各接触面间的动摩擦因数均为μ，砝码到纸板左端的距离和到桌面右端的距离均为d。现用水平向右的恒定拉力F拉动纸板，下列说法正确的是(　　)

A．纸板相对砝码运动时，纸板所受摩擦力的大小为μ(M＋m)g
B．要使纸板相对砝码运动，F一定大于2μ(M＋m)g
C．若砝码与纸板分离时的速度小于，砝码不会从桌面上掉下
D．当F＝μ(2M＋3m)g时，砝码恰好到达桌面边缘
答案　BC
解析　对纸板分析，当纸板相对砝码运动时，纸板所受的摩擦力为μ(M＋m)g＋μMg，故A错误；设砝码的加速度为a1，纸板的加速度为a2，则有μMg＝Ma1，F－μMg－μ(M＋m)g＝ma2，发生相对运动需要a2>a1，代入数据解得F>2μ(M＋m)g，故B正确；若砝码与纸板分离时的速度小于，砝码匀加速运动的位移小于＝＝，匀减速运动的位移小于＝＝，则总位移小于d，不会从桌面上掉下，故C正确；当F＝μ(2M＋3m)g时，砝码未脱离纸板时的加速度a1＝μg，纸板的加速度a2＝＝2μg，根据a2t2－a1t2＝d，解得t＝，则砝码脱离纸板时的速度v＝a1t＝，砝码脱离纸板后做匀减速运动，匀减速运动的加速度大小a′＝μg，则匀减速运动的位移x′＝＝＝d，而匀加速运动的位移x＝a1t2＝d，可知砝码离开桌面，D错误。
8．(2018·湖南怀化质检)如图所示，水平地面上放置一个质量为m的物体，在与水平方向成θ角、斜向右上方的拉力F的作用下沿水平地面运动。物体与地面间的动摩擦因数为μ，重力加速度为g。求：

(1)若物体在拉力F的作用下能始终沿水平面向右运动且不脱离地面，拉力F的大小范围；
(2)已知m＝10 kg，μ＝0.5，g取10 m/s2，若F的方向可以改变，求使物体以恒定加速度a＝5 m/s2向右做匀加速直线运动时，拉力F的最小值。
答案　(1)≤F≤　(2)40 N
解析　(1)要使物体运动时不离开地面，应有：
Fsinθ≤mg，
要使物体能一直向右运动，应有：Fcosθ≥μ(mg－Fsinθ)
联立解得：≤F≤。
(2)根据牛顿第二定律得Fcosθ－μ(mg－Fsinθ)＝ma
解得：F＝。
设sinα＝，cosα＝
则F＝
＝
上式变形得F＝，
其中α＝arcsin，
当sin(θ＋α)＝1时，F有最小值，
解得：Fmin＝，
代入相关数据解得：Fmin＝40 N。
9. (2018·山东济宁模拟)如图所示，一儿童玩具静止在水平地面上，一名幼儿用沿与水平面成30°角的恒力拉着它沿水平地面运动，已知拉力F＝6.5 N，玩具的质量m＝1 kg，经过时间t＝2.0 s，玩具移动了距离x＝2 m，这时幼儿将手松开，玩具又滑行了一段距离后停下。(g取10 m/s2)求：

(1)玩具与地面间的动摩擦因数；
(2)松开后玩具还能滑行多远？
(3)当力F与水平方向夹角θ为多少时拉力F最小？
答案　(1)　(2) m　(3)30°
解析　(1)玩具做初速度为零的匀加速直线运动，由位移公式可得x＝at2，解得a＝ m/s2，
对玩具，由牛顿第二定律得
Fcos30°－μ(mg－Fsin30°)＝ma，
解得μ＝。
(2)松手时，玩具的速度v＝at＝2 m/s，
松手后，由牛顿第二定律得μmg＝ma′
解得a′＝ m/s2，
由匀变速运动的速度位移公式得
玩具的位移x′＝＝ m。
(3)当拉力与水平方向的夹角为θ时，玩具要在水平面上运动，则Fcosθ－Ff>0，
Ff＝μFN，
在竖直方向上，由平衡条件得FN＋Fsinθ＝mg，
解得F>，
因为cosθ＋μsinθ＝sin(60°＋θ)，
所以当θ＝30°时，拉力最小。
10．(2018·陕西渭南调研)如图所示，静止在光滑水平面上的斜面体，质量为M，倾角为α，其斜面上有一静止的滑块，质量为m，两者之间的动摩擦因数为μ，滑块受到的最大静摩擦力可认为等于滑动摩擦力，重力加速度为g。现给斜面体施加水平向右的力使斜面体加速运动，求：

(1)若要使滑块与斜面体一起加速运动，图中水平向右的力F的最大值；
(2)若要使滑块做自由落体运动，图中水平向右的力F的最小值。
答案　(1)　(2)
解析　(1)当滑块与斜面体一起向右加速时，力F越大，加速度越大，当F最大时，斜面体对滑块的静摩擦力达到最大值Ffm，滑块受力如图所示。

设一起加速的最大加速度为a，对滑块应用牛顿第二定律得：
FNcosα＋Ffmsinα＝mg，①
Ffmcosα－FNsinα＝ma，②
由题意知Ffm＝μFN，③
联立解得a＝g，
对整体受力分析Fmax＝(M＋m)a，
联立解得Fmax＝。
(2)要使滑块做自由落体运动，滑块与斜面体之间没有力的作用，滑块的加速度为g，设此时M的加速度为aM，
当水平向右的力F最小时，二者没有相互作用但仍接触，
则有＝tanα，即＝tanα，
则对M：Fmin＝MaM，联立解得Fmin＝。