2020版新一线高考理科数学（北师大版）一轮复习教学案：第6章第1节不等式的性质与一元二次不等式

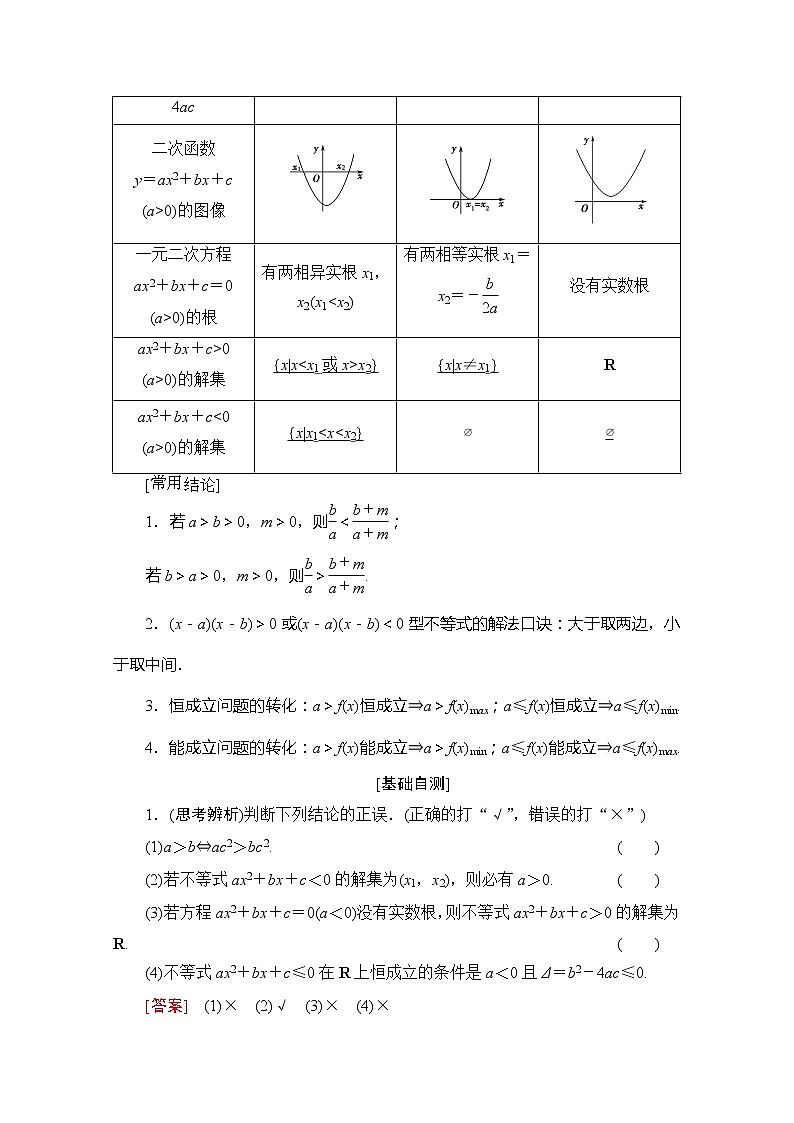
第章　不等式、推理与证明第一节　不等式的性质与一元二次不等式[考纲传真]　1.了解现实世界和日常生活中存在着大量的不等关系，了解不等式(组)的实际背景.2.会从实际问题的情境中抽象出一元二次不等式模型.3.通过函数图像了解一元二次不等式与相应的二次函数、一元二次方程的联系.4.会解一元二次不等式，对给定的一元二次不等式，会设计求解的程序框图．1．两个实数比较大小的方法(1)作差法(2)作商法2．不等式的性质(1)对称性：a>b⇔b<a；(2)传递性：a>b，b>c⇒a>c；(3)可加性：a>b⇔a＋c>b＋c；a>b，c>d⇒a＋c>b＋d；(4)可乘性：a>b，c>0⇒ac>bc；a>b，c<0⇒ac<bc；a>b>0，c>d>0⇒ac>bd；(5)乘方法则：a>b>0⇒an>bn(n≥2，n∈N)；(6)开方法则：a>b>0⇒>(n≥2，n∈N)；(7)倒数性质：设ab>0，则a<b⇔>.3．“三个二次”的关系判别式Δ＝b2－4acΔ>0Δ＝0Δ<0二次函数y＝ax2＋bx＋c(a>0)的图像一元二次方程ax2＋bx＋c＝0(a>0)的根有两相异实根x1，x2(x1<x2)有两相等实根x1＝x2＝－没有实数根ax2＋bx＋c>0(a>0)的解集{x|x<x1或x>x2}{x|x≠x1}Rax2＋bx＋c<0(a>0)的解集{x|x1<x<x2}∅∅1．若a＞b＞0，m＞0，则＜；若b＞a＞0，m＞0，则＞.2．(x－a)(x－b)＞0或(x－a)(x－b)＜0型不等式的解法口诀：大于取两边，小于取中间．3．恒成立问题的转化：a＞f(x)恒成立⇒a＞f(x)max；a≤f(x)恒成立⇒a≤f(x)min.4．能成立问题的转化：a＞f(x)能成立⇒a＞f(x)min；a≤f(x)能成立⇒a≤f(x)max.[基础自测]1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”)(1)a＞b⇔ac2＞bc2.  (　　)(2)若不等式ax2＋bx＋c＜0的解集为(x1，x2)，则必有a＞0. (　　)(3)若方程ax2＋bx＋c＝0(a＜0)没有实数根，则不等式ax2＋bx＋c＞0的解集为R.               (　　)(4)不等式ax2＋bx＋c≤0在R上恒成立的条件是a＜0且Δ＝b2－4ac≤0.                              (　　)[答案]　(1)×　(2)√　(3)×　(4)×2．(教材改编)设A＝(x－3)2，B＝(x－2)(x－4)，则A与B的大小关系为(　　)A．A≥B　　　　　 B．A＞BC．A≤B   D．A＜BB　[∵A－B＝(x－3)2－(x－2)(x－4)＝x2－6x＋9－x2＋6x－8＝1＞0，∴A＞B，故选B．]3．(教材改编)若a＞b＞0，c＜d＜0，则一定有(　　)A.＞   B．＜C.＞   D．＜B　[∵c＜d＜0，∴－c＞－d＞0，∵a＞b＞0，∴－ac＞－bd，∴－＞－，即＜.故选B．]4．不等式－x2－3x＋4>0的解集为________．(用区间表示)(－4,1)　[由－x2－3x＋4>0得x2＋3x－4<0，解得－4<x<1，所以不等式－x2－3x＋4>0的解集为(－4,1)．]5．(教材改编)若不等式ax2＋bx＋2＞0的解集为，则a＋b＝________.－14　[由题意知x1＝－，x2＝是方程ax2＋bx＋2＝0的两个根，则解得(经检验知满足题意)．∴a＋b＝－14.]比较大小及不等式性质的应用1．设α∈，β∈[0，π]，那么2α－的取值范围是(　　)A.　　　　　　 B．C.   D．D　[∵α∈，β∈[0，π]，∴2α∈，∈，即－＜2α＜π，－≤－≤0.∴－＜2α－＜π，故选D．]2．已知a，b，c满足c＜b＜a，且ac＜0，那么下列选项中一定成立的是(　　)A．ab＞ac   B．c(b－a)＜0C．cb2＜ab2   D．ac(a－c)＞0A　[∵c＜b＜a，且ac＜0，∴c＜0，a＞0，∴ac＜ab，即A选项正确．]3．设f(x)＝ax2＋bx，若1≤f(－1)≤2,3≤f(1)≤4，则f(－2)的取值范围是________．[6,10]　[法一：(待定系数法)由题意知f(－2)＝4a－2b，设存在实数m，n，使得4a－2b＝m(a＋b)＋n(a－b)，即4a－2b＝(m＋n)a＋(m－n)b，所以解得所以f(－2)＝4a－2b＝(a＋b)＋3(a－b)．又3≤a＋b≤4,3≤3(a－b)≤6，所以6≤(a＋b)＋3(a－b)≤10，即f(－2)的取值范围是[6,10]．法二：(运用方程思想)由得所以f(－2)＝4a－2b＝3f(－1)＋f(1)．又所以6≤3f(－1)＋f(1)≤10，即f(－2)的取值范围是[6,10]．][规律方法]　1.用同向不等式求差范围的技巧⇒⇒a－d＜x－y＜b－c.这种方法在三角函数中求角的范围时经常用到．2．比较大小的三种常用方法(1)作差法：直接作差判断正负即可．(2)作商法：直接作商与1的大小比较，注意两式的符号．(3)函数的单调性法：把比较的两个数看成一个函数的两个值，根据函数的单调性比较．一元二次不等式的解法【例1】　解下列不等式：(1)3＋2x－x2≥0；(2)x2－(a＋1)x＋a<0.[解]　(1)原不等式化为x2－2x－3≤0，即(x－3)(x＋1)≤0，故所求不等式的解集为{x|－1≤x≤3}．(2)原不等式可化为(x－a)(x－1)<0，当a>1时，原不等式的解集为(1，a)；当a＝1时，原不等式的解集为∅；当a<1时，原不等式的解集为(a,1)．[母题探究]　将本例(2)中不等式改为ax2－(a＋1)x＋1<0，求不等式的解集．[解]　若a＝0，原不等式等价于－x＋1<0，解得x>1.若a<0，原不等式等价于(x－1)>0，解得x<或x>1.若a>0，原不等式等价于(x－1)<0.①当a＝1时，＝1，(x－1)<0无解；②当a>1时，<1，解(x－1)<0得<x<1；③当0<a<1时，>1，解 (x－1)<0得1<x<.综上所述：当a<0时，解集为；当a＝0时，解集为{x|x>1}；当0<a<1时，解集为；当a＝1时，解集为∅；当a>1时，解集为.[规律方法]　1.解一元二次不等式的一般方法和步骤：(1)化：把不等式变形为二次项系数大于零的标准形式．(2)判：计算对应方程的判别式，根据判别式判断方程有没有实根(无实根时，不等式解集为R或∅)．(3)求：求出对应的一元二次方程的根．(4)写：利用“大于取两边，小于取中间”写出不等式的解集．2．解含参数的一元二次不等式的步骤：(1)二次项中若含有参数应讨论是等于0，小于0，还是大于0，然后将不等式转化为一次不等式或二次项系数为正的形式．(2)判断方程的根的个数，讨论判别式Δ与0的关系．(3)确定无根时可直接写出解集，确定方程有两个根时，要讨论两根的大小关系，从而确定解集形式． (1)已知不等式ax2－bx－1>0的解集是，则不等式x2－bx－a≥0的解集是(　　)A．{x|2<x<3}B．{x|x≤2或x≥3}C.D．(2)不等式≥－1的解集为________．(1)B　(2)　　[(1)∵不等式ax2－bx－1>0的解集是，∴ax2－bx－1＝0的解是x1＝－和x2＝－，且a<0，∴解得则不等式x2－bx－a≥0即为x2－5x＋6≥0，解得x≤2或x≥3.(2)将原不等式移项通分得≥0，等价于解得x≤或x＞5.∴原不等式的解集为.]一元二次不等式恒成立问题►考法1　在R上恒成立，求参数的范围【例2】　不等式(a－2)x2＋2(a－2)x－4<0对一切x∈R恒成立，则实数a的取值范围是________．(－2,2]　[当a－2＝0，即a＝2时，不等式即为－4<0，对一切x∈R恒成立，当a≠2时，则有即∴－2<a<2.综上，可得实数a的取值范围是(－2,2]．]►考法2　在指定区间上恒成立，求参数的范围【例3】　设函数f(x)＝mx2－mx－1.若对于x∈[1,3]，f(x)<－m＋5恒成立，求m的取值范围．[解]　要使f(x)<－m＋5在x∈[1,3]上恒成立，即m2＋m－6<0在x∈[1,3]上恒成立．有以下两种方法：法一：令g(x)＝m2＋m－6，x∈[1,3]．当m>0时，g(x)在[1,3]上是增函数，所以g(x)max＝g(3)⇒7m－6<0，所以m<，所以0<m<；当m＝0时，－6<0恒成立；当m<0时，g(x)在[1,3]上是减函数，所以g(x)max＝g(1)⇒m－6<0，所以m<6，所以m<0.综上所述：m的取值范围是.法二：因为x2－x＋1＝2＋>0，又因为m(x2－x＋1)－6<0，所以m<.因为函数y＝＝在[1,3]上的最小值为，所以只需m<即可．所以m的取值范围是.►考法3　变换主元，求x的范围【例4】　对任意的k∈[－1,1]，函数f(x)＝x2＋(k－4)x＋4－2k的值恒大于零，则x的取值范围是__________．{x|x<1或x>3}　[对任意的k∈[－1,1]，x2＋(k－4)x＋4－2k>0恒成立，即g(k)＝(x－2)k＋(x2－4x＋4)>0，在k∈[－1,1]时恒成立．只需g(－1)>0且g(1)>0，即解得x<1或x>3.][规律方法]　一元二次不等式恒成立问题的求解思路(1)形如f(x)＞0或f(x)＜0(x∈R)的不等式确定参数的范围时，结合一元二次方程，利用判别式来求解．(2)形如f(x)＞0或f(x)＜0(x∈[a，b])的不等式确定参数范围时，常转化为求二次函数的最值或用分离参数法求最值．(3)形如f(x)＞0或f(x)＜0(参数m∈[a，b])的不等式确定x的范围时，要注意变换主元，一般地，知道谁的范围，就选谁当主元，求谁的范围，谁就是参数． (1)若不等式x2＋ax－2＞0在区间[1,5]上有解，则实数a的取值范围是________．(2)求使不等式x2＋(a－6)x＋9－3a＞0(|a|≤1)恒成立的x的取值范围．(1)　[设f(x)＝x2＋ax－2，由题知Δ＝a2＋8＞0，所以方程x2＋ax－2＝0恒有一正一负两根，于是不等式x2＋ax－2＞0在区间[1,5]上有解的充要条件是f(5)＞0，即a∈.](2)[解]　将原不等式整理为形式上是关于a的不等式(x－3)a＋x2－6x＋9＞0.令f(a)＝(x－3)a＋x2－6x＋9，因为f(a)＞0在|a|≤1时恒成立，所以(1)若x＝3，则f(a)＝0，不符合题意，舍去．(2)若x≠3，则由一次函数的单调性，可得即解得x＜2或x＞4.综上可知，使原不等式恒成立的x的取值范围是(－∞，2)∪(4，＋∞)．1．(2016·全国卷Ⅰ)设集合A＝{x|x2－4x＋3<0}，B＝{x|2x－3>0}，则A∩B＝(　　)A.　　　　　　 B．C.   D．D　[∵x2－4x＋3＜0，∴1＜x＜3，∴A＝{x|1＜x＜3}．∵2x－3＞0，∴x＞，∴B＝.∴A∩B＝{x|1＜x＜3}∩＝.故选D．]2.(2016·全国卷Ⅲ)设集合S＝{x|(x－2)(x－3)≥0}，T＝{x|x>0}，则S∩T＝(　　)A．[2,3]   B．(－∞，2]∪[3，＋∞)C．[3，＋∞)   D．(0,2]∪[3，＋∞)D　[由题意知S＝{x|x≤2或x≥3}，则S∩T＝{x|0＜x≤2或x≥3}．故选D．]