2021版江苏高考数学一轮复习讲义：第4章第4节　三角函数的图象与性质

第四节　三角函数的图象与性质
[最新考纲]　1.能画出y＝sin x，y＝cos x，y＝tan x的图象，了解三角函数的周期性.2.理解正弦函数、余弦函数在[0,2π]上的性质(如单调性、最大值和最小值、图象与x轴的交点等)，理解正切函数在区间内的单调性．


1．用五点法作正弦函数和余弦函数的简图
正弦函数y＝sin x，x∈[0,2π]图象的五个关键点是：(0,0)，，(π，0)，，(2π，0)．
余弦函数y＝cos x，x∈[0,2π]图象的五个关键点是：(0,1)，，(π，－1)，，(2π，1)．
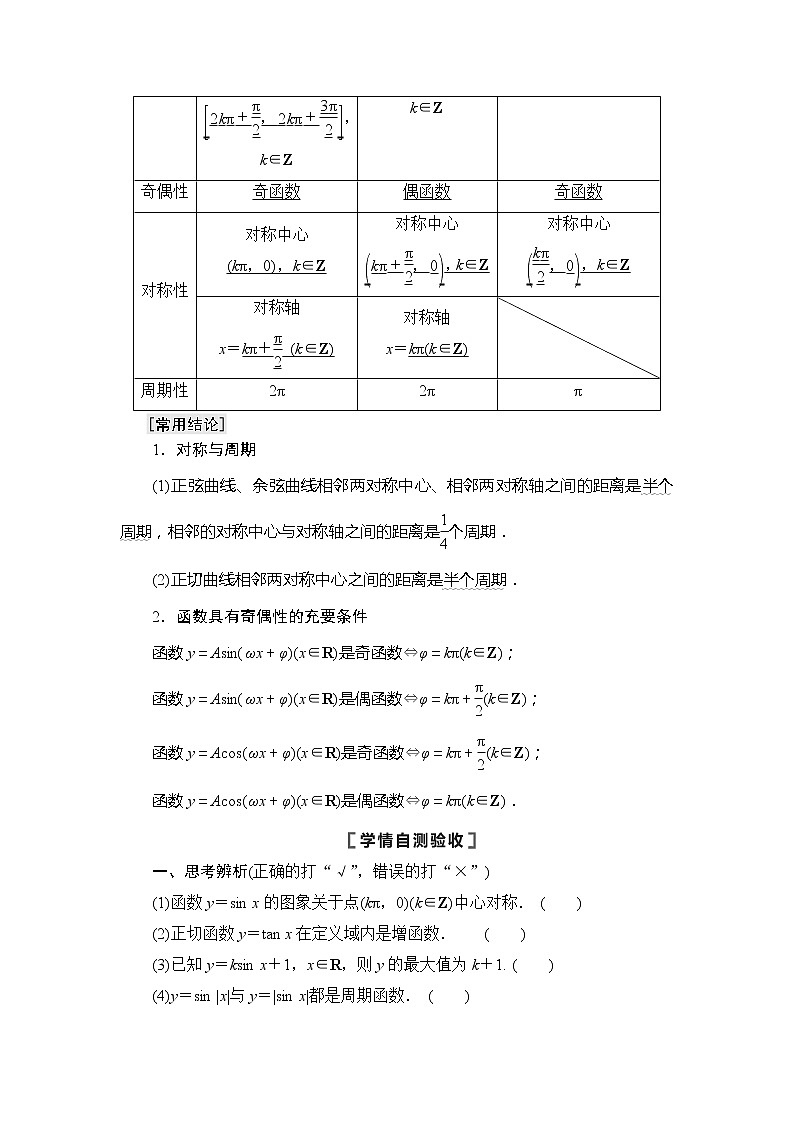
2．正弦函数、余弦函数、正切函数的图象与性质
函数
y＝sin x
y＝cos x
y＝tan x
图象



定义域
R
R

值域
[－1,1]
[－1,1]
R
单调性
递增区间：
，
k∈Z，
递减区间：
，
k∈Z
递增区间：
[2kπ－π，2kπ]，
k∈Z，
递减区间：
[2kπ，2kπ＋π]，
k∈Z
递增区间
，
k∈Z
奇偶性
奇函数
偶函数
奇函数
对称性
对称中心
(kπ，0)，k∈Z
对称中心
，k∈Z
对称中心
，k∈Z
对称轴
x＝kπ＋ (k∈Z)
对称轴
x＝kπ(k∈Z)

周期性
2π
2π
π

1．对称与周期
(1)正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是半个周期，相邻的对称中心与对称轴之间的距离是个周期．
(2)正切曲线相邻两对称中心之间的距离是半个周期．
2．函数具有奇偶性的充要条件
函数y＝Asin(ωx＋φ)(x∈R)是奇函数⇔φ＝kπ(k∈Z)；
函数y＝Asin(ωx＋φ)(x∈R)是偶函数⇔φ＝kπ＋(k∈Z)；
函数y＝Acos(ωx＋φ)(x∈R)是奇函数⇔φ＝kπ＋(k∈Z)；
函数y＝Acos(ωx＋φ)(x∈R)是偶函数⇔φ＝kπ(k∈Z)．

一、思考辨析(正确的打“√”，错误的打“×”)
(1)函数y＝sin x的图象关于点(kπ，0)(k∈Z)中心对称． (　　)
(2)正切函数y＝tan x在定义域内是增函数． (　　)
(3)已知y＝ksin x＋1，x∈R，则y的最大值为k＋1. (　　)
(4)y＝sin |x|与y＝|sin x|都是周期函数． (　　)
[答案](1)√　(2)×　(3)×　(4)×
二、教材改编
1．函数y＝tan 2x的定义域是(　　)
A.
B.
C.
D.
D　[由2x≠kπ＋，k∈Z，得x≠＋，k∈Z，
∴y＝tan 2x的定义域为.]
2．函数f(x)＝cos的最小正周期是 ．
π　[T＝＝π.]
3．y＝sin的单调减区间是 ．
(k∈Z)　[由＋2kπ≤2x－≤＋2kπ，k∈Z得
＋kπ≤x≤＋kπ，k∈Z.]
4．y＝3sin在区间上的值域是 ．


考点1　三角函数的定义域和值域
　1.三角函数定义域的求法
求三角函数定义域实际上是构造简单的三角不等式(组)，常借助三角函数线或三角函数图象来求解．
2．求三角函数最值或值域的常用方法
(1)直接法：直接利用sin x和cos x的值域求解．
(2)化一法：把所给三角函数化为y＝Asin(ωx＋φ)＋k的形式，由正弦函数单调性写出函数的值域．
(3)换元法：把sin x，cos x，sin xcos x或sin x±cos x换成t，转化为二次函数求解．
　1.函数f(x)＝－2tan的定义域是(　　)

D　[由正切函数的定义域，得2x＋≠kπ＋，k∈Z，
即x≠＋(k∈Z)，故选D.]
2．(2019·全国卷Ⅰ)函数f(x)＝sin－3cos x的最小值为 ．
－4　[f(x)＝sin－3cos x＝－cos 2x－3cos x＝－2cos2x－3cos x＋1，
令cos x＝t，则t∈[－1,1]．
f(t)＝－2t2－3t＋1＝－2＋，
易知当t＝1时，f(t)min＝－2×12－3×1＋1＝－4.
故f(x)的最小值为－4.]
3．已知函数f(x)＝2asin＋a＋b(a＜0)的定义域为，值域为[－5,1]，则a＋b＝ .
－1　[因为x∈，所以2x＋∈，所以sin∈.因为a＜0，所以f(x)∈[3a＋b，b]．因为函数的值域为[－5,1]，所以3a＋b＝－5，b＝1，所以a＝－2，所以a＋b＝－1.]
4．函数y＝sin x－cos x＋sin xcos x的值域为 ．
　[设t＝sin x－cos x，则t2＝sin2x＋cos2x－2sin x·cos x，sin xcos x＝，且－≤t≤.
∴y＝－＋t＋＝－(t－1)2＋1，t∈[－，]．
当t＝1时，ymax＝1；
当t＝－时，ymin＝－－.
∴函数的值域为.]
　求解三角函数的值域(最值)常见的几种类型
(1)形如y＝asin x＋bcos x＋c的三角函数化为y＝Asin(ωx＋φ)＋c的形式，再求值域(最值)．
(2)形如y＝asin2x＋bsin x＋c的三角函数，可先设sin x＝t，化为关于t的二次函数求值域(最值)．
(3)形如y＝asin3x＋bsin2x＋csin x＋d，类似于(2)进行换元，然后用导数法求最值．
考点2　三角函数的单调性
(1)形如y＝Asin(ωx＋φ)的函数的单调性问题，一般是将ωx＋φ看成一个整体，再结合图象利用y＝sin x的单调性求解；(2)如果函数中自变量的系数为负值，要根据诱导公式把自变量系数化为正值，再确定其单调性．
　求三角函数的单调性
(1)函数f(x)＝tan的单调递增区间是(　　)

(2)(2019·大连模拟)函数y＝sin x＋cos x的单调递增区间是 ．
(1)B　(2) 　[(1)由kπ－＜2x－＜kπ＋(k∈Z)，
得－＜x＜＋(k∈Z)，
所以函数f(x)＝tan的单调递增区间为(k∈Z)，故选B.
(2)∵y＝sin x＋cos x＝sin，
由2kπ－≤x＋≤2kπ＋(k∈Z)，
解得2kπ－≤x≤2kπ＋(k∈Z)．
∴函数的单调递增区间为 (k∈Z)，
又x∈，∴单调递增区间为.]
　本例(2) 在整体求得函数y＝sin x＋cos x的增区间后，采用对k赋值的方式求得x∈上的区间．
　根据函数的单调性求参数
(1)已知ω＞0，函数f(x)＝sin在上单调递减，则ω的取值范围是(　　)
A．(0,2]　　　　　　 B.
C. D.
(2)(2018·全国卷Ⅱ)若f(x)＝cos x－sin x在[0，a] 是减函数，则a的最大值是(　　)
A.　　　B. C.　　　D．π
(1)D　(2)C　[(1)由2kπ＋≤ωx＋≤2kπ＋，得＋≤x≤＋，k∈Z，
因为f(x)＝sin在上单调递减，
所以解得因为k∈Z，ω＞0，所以k＝0，
所以≤ω≤，即ω的取值范围为.故选D.
(2)f(x)＝cos x－sin x＝－sin，
当x－∈，即x∈时，
sin单调递增，－sin 单调递减，
∴是f(x)在原点附近的单调递减区间，
结合条件得[0，a]⊆，
∴a≤，即amax＝，故选C.]
　已知单调区间求参数范围的3种方法
子集法
求出原函数的相应单调区间，由已知区间是所求某区间的子集，列不等式(组)求解
反子集法
由所给区间求出整体角的范围，由该范围是某相应正、余弦函数的某个单调区间的子集，列不等式(组)求解
周期性法
由所给区间的两个端点到其相应对称中心的距离不超过周期列不等式(组)求解
　1.若函数f(x)＝sin ωx(ω＞0)在区间上单调递增，在区间上单调递减，则ω＝ .
　[由已知得＝，∴T＝，∴ω＝＝.]
2．函数f(x)＝sin的单调减区间为 ．
　[由已知，得函数为y＝－sin，欲求函数的单调减区间，只需求y＝sin的单调增区间即可．
由2kπ－≤2x－≤2kπ＋，k∈Z，
得kπ－≤x≤kπ＋，k∈Z.
故所求函数的单调减区间为 (k∈Z)．]
考点3　三角函数的周期性、奇偶性、对称性
　求解三角函数y＝sin(ωx＋φ)(ω＞0)的周期性、奇偶性、对称性问题，其实质都是根据y＝sin x的对应性质，利用整体代换的思想求解．
　三角函数的周期性
(1)(2019·全国卷Ⅱ)下列函数中，以为周期且在区间单调递增的是(　　)
A．f(x)＝|cos 2x| B．f(x)＝|sin 2x|
C．f(x)＝cos|x| D．f(x)＝sin|x|
(2)若函数f(x)＝2tan的最小正周期T满足1＜T＜2，则自然数k的值为 ．
(1)A　(2)2或3　[(1)对于选项A，作出y＝|cos 2x|的部分图象，如图1所示，则f(x)在上单调递增，且最小正周期T＝，故A正确．
对于选项B，作出f(x)＝|sin 2x|的部分图象，如图2所示，则f(x)在上单调递减，且最小正周期T＝，故B不正确．对于选项C，∵f(x)＝cos|x|＝cos x，∴最小正周期T＝2π，故C不正确．
对于选项D，作出f(x)＝sin|x|的部分图象，如图3所示．显然f(x)不是周期函数，故D不正确．故选A.
　　
图1　　　　　　　　　　图2
]
图3
(2)由题意得，1＜＜2，∴k＜π＜2k，即＜k＜π，
又k∈Z，∴k＝2或3.]
　公式莫忘绝对值，对称抓住“心”与“轴”
(1)公式法求周期
①正弦型函数f(x)＝Asin(ωx＋φ)＋B的周期T＝；
②余弦型函数f(x)＝Acos(ωx＋φ)＋B的周期T＝；
③正切型函数f(x)＝Atan(ωx＋φ)＋B的周期T＝.
(2)对称性求周期
①两对称轴距离的最小值等于；
②两对称中心距离的最小值等于；
③对称中心到对称轴距离的最小值等于.
(3)特征点法求周期
①两个最大值点之差的最小值等于T；
②两个最小值点之差的最小值等于T；
③最大值点与最小值点之差的最小值等于.
特征点法求周期实质上就是由图象的对称性求周期，因为最值点与函数图象的对称轴相对应．(说明：此处的T均为最小正周期)
　三角函数的奇偶性
　已知函数f(x)＝3sin，φ∈(0，π)．
(1)若f(x)为偶函数，则φ＝ ；
(2)若f(x)为奇函数，则φ＝ .
(1)π　(2)　[(1)因为f(x)＝3sin为偶函数，
所以－＋φ＝kπ＋，k∈Z，
又因为φ∈(0，π)，所以φ＝.
(2)因为f(x)＝3sin为奇函数，
所以－＋φ＝kπ，k∈Z，
又φ∈(0，π)，
所以φ＝.]
　若f(x)＝Asin(ωx＋φ)(A，ω≠0)，则①f(x)为偶函数的充要条件是φ＝＋kπ(k∈Z)；②f(x)为奇函数的充要条件是φ＝kπ(k∈Z)．
　三角函数的对称性
(1)已知函数f(x)＝2sin(ω＞0)的最小正周期为4π，则该函数的图象(　　)
A．关于点对称
B．关于点对称
C．关于直线x＝对称
D．关于直线x＝对称
(2)已知函数y＝sin(2x＋φ)的图象关于直线x＝对称，则φ的值为 ．
(1)B　(2)－　[(1)因为函数f(x)＝2sin(ω＞0)的最小正周期是4π，而T＝＝4π，所以ω＝，
即f(x)＝2sin.
令＋＝＋kπ(k∈Z)，解得x＝＋2kπ(k∈Z)，
故f(x)的对称轴为x＝＋2kπ(k∈Z)，
令＋＝kπ(k∈Z)，解得x＝－＋2kπ(k∈Z)．
故f(x)的对称中心为(k∈Z)，对比选项可知B正确．
(2)由题意得f＝sin＝±1，
∴＋φ＝kπ＋(k∈Z)，∴φ＝kπ－(k∈Z)．
∵φ∈，∴φ＝－.]
　三角函数图象的对称轴和对称中心的求解方法
若求f(x)＝Asin(ωx＋φ)(ω≠0)图象的对称轴，则只需令ωx＋φ＝＋kπ(k∈Z)，求x；若求f(x)＝Asin(ωx＋φ)(ω≠0)图象的对称中心的横坐标，则只需令ωx＋φ＝kπ(k∈Z)，求x.
　1.设函数f(x)＝cos，则下列结论错误的是(　　)
A．f(x)的一个周期为－2π
B．y＝f(x)的图象关于直线x＝对称
C．f(x＋π)的一个零点为x＝
D．f(x)在上单调递减
D　[A项，因为f(x)＝cos的周期为2kπ(k∈Z)，所以f(x)的一个周期为－2π，A项正确；
B项，因为f(x)＝cos图象的对称轴为直线x＝kπ－(k∈Z)，所以y＝f(x)的图象关于直线x＝对称，B项正确；
C项，f(x＋π)＝cos.令x＋＝kπ＋(k∈Z)，得x＝kπ－，当k＝1时，x＝，
所以f(x＋π)的一个零点为x＝，C项正确；
D项，因为f(x)＝cos的单调递减区间为2kπ－，2kπ＋(k∈Z)，
单调递增区间为2kπ＋，2kπ＋(k∈Z)，
所以是f(x)的单调递减区间，，π是f(x)的单调递增区间，D项错误．]
2．(2019·成都模拟)已知函数f(x)＝sin(ωx＋φ)的最小正周期为4π，且∀x∈R，有f(x)≤f成立，则f(x)图象的一个对称中心坐标是(　　)
A. B.
C. D.
A　[由f(x)＝sin(ωx＋φ)的最小正周期为4π，得ω＝.
因为f(x)≤f恒成立，
所以f(x)max＝f，
即×＋φ＝＋2kπ(k∈Z)，
由|φ|＜，得φ＝，
故f(x)＝sin.
令x＋＝kπ(k∈Z)，得x＝2kπ－(k∈Z)，
故f(x)图象的对称中心为(k∈Z)，
当k＝0时，f(x)图象的对称中心为.]