2019版高考数学（理）一轮精选教师用书人教通用：第4章5第5讲　三角函数的图象与性质

第5讲　三角函数的图象与性质

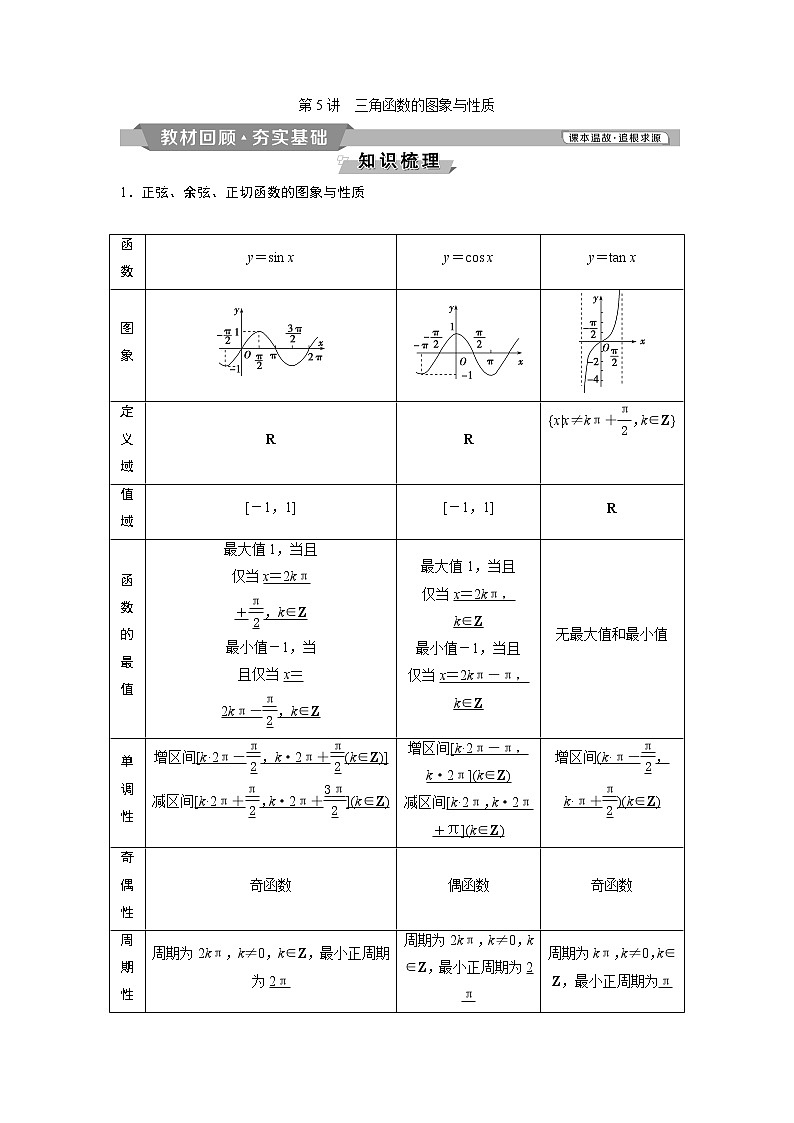
1．正弦、余弦、正切函数的图象与性质

函数
y＝sin x
y＝cos x
y＝tan x
图象



定义域
R
R
{x|x≠kπ＋，k∈Z}
值域
[－1，1]
[－1，1]
R
函数的最值
最大值1，当且
仅当x＝2kπ
＋，k∈Z
最小值－1，当
且仅当x＝
2kπ－，k∈Z
最大值1，当且
仅当x＝2kπ，
k∈Z　　　　
最小值－1，当且
仅当x＝2kπ－π，
k∈Z
无最大值和最小值
单调性
增区间[k·2π－，k·2π＋(k∈Z)]
减区间[k·2π＋，k·2π＋](k∈Z)
增区间[k·2π－π，k·2π](k∈Z)
减区间[k·2π，k·2π＋π](k∈Z)
增区间(k·π－，k·π＋)(k∈Z)
奇偶性
奇函数
偶函数
奇函数
周期性
周期为2kπ，k≠0，k∈Z，最小正周期为2π
周期为2kπ，k≠0，k∈Z，最小正周期为2π
周期为kπ，k≠0，k∈Z，最小正周期为π
对称性
对称中心
(kπ，0)，k∈Z
，k∈Z
，k∈Z
对称轴
x＝kπ＋，k∈Z
x＝kπ，k∈Z
无对称轴
零点
kπ，k∈Z
kπ＋，k∈Z
kπ，k∈Z
2.周期函数的定义
对于函数f(x)，如果存在一个非零常数T，使得当x取定义域内的每一个值时，都有f(x＋T)＝f(x)，那么函数f(x)就叫做周期函数，非零常数T叫做这个函数的周期；函数y＝Asin(ωx＋φ)和y＝Acos(ωx＋φ)的周期均为T＝；函数y＝Atan(ωx＋φ)的周期为T＝.
3．对称与周期
正弦曲线、余弦曲线相邻的两个对称中心、相邻的两条对称轴之间的距离是半个周期，相邻的对称中心与对称轴之间的距离是四分之一个周期；正切曲线相邻的两个对称中心之间的距离是半个周期．

判断正误(正确的打“√”，错误的打“×”)
(1)y＝cos x在第一、二象限内是减函数．(　　)
(2)若y＝ksin x＋1，x∈R，则y的最大值是k＋1.(　　)
(3)若非零实数T是函数f(x)的周期，则kT(k是非零整数)也是函数f(x)的周期．(　　)
(4)函数y＝sin x图象的对称轴方程为x＝2kπ＋(k∈Z)．(　　)
(5)函数y＝tan x在整个定义域上是增函数．(　　)
答案：(1)×　(2)×　(3)√　(4)×　(5)×
函数y＝tan 3x的定义域为(　　)
A.
B.
C.
D.
解析：选D.由3x≠＋kπ(k∈Z)，得x≠＋，k∈Z.故选D.
(2017·高考全国卷Ⅲ)设函数f(x)＝cos(x＋)，则下列结论错误的是(　　)
A．f(x)的一个周期为－2π
B．y＝f(x)的图象关于直线x＝对称
C．f(x＋π)的一个零点为x＝
D．f(x)在(，π)单调递减
解析：选D.根据函数解析式可知函数f(x)的最小正周期为2π，所以函数的一个周期为－2π，A正确；当x＝时，x＋＝3π，所以cos＝－1，所以B正确；f(x＋π)＝cos＝cos，当x＝时，x＋＝，所以f(x＋π)＝0，所以C正确；函数f(x)＝cos在上单调递减，在上单调递增，故D不正确．所以选D.
函数y＝3－2cos的最大值为__________，此时x＝________．
解析：函数y＝3－2cos的最大值为3＋2＝5，此时x＋＝π＋2kπ(k∈Z)，即x＝＋2kπ(k∈Z)．
答案：5　＋2kπ(k∈Z)
函数f(x)＝sin，x∈[0，π]的减区间为________．
解析：当2kπ＋≤x＋≤2kπ＋，k∈Z，
即2kπ＋≤x≤2kπ＋，k∈Z时，函数f(x)是减函数．
又x∈[0，π]，所以f(x)的单调递减区间为.
答案：


　　　　　　三角函数的定义域和值域
[典例引领]
(1)(2017·高考全国卷Ⅱ)函数f(x)＝sin2x＋cos x－的最大值是________．
(2)函数y＝lg(2sin x－1)＋的定义域是________．
【解析】　(1)依题意，f(x)＝sin2x＋cos x－＝－cos2x＋cos x＋＝－＋1，因为x∈，所以cos x∈[0，1]，因此当cos x＝时，f(x)max＝1.
(2)要使函数y＝lg(2sin x－1)＋有意义，
则即
解得2kπ＋≤x<2kπ＋，k∈Z.
即函数的定义域为，k∈Z.
【答案】　(1)1　(2)，k∈Z

(1)三角函数定义域的求法
求三角函数定义域实际上是构造简单的三角不等式(组)，常借助三角函数线或三角函数图象来求解．
(2)三角函数值域的不同求法
①利用sin x和cos x的值域直接求．
②把所给的三角函数式变换成y＝Asin(ωx＋φ)的形式求值域．
③(换元法)把sin x或cos x看作一个整体，转换成二次函数求值域．
④(换元法)利用sin x±cos x和sin xcos x的关系转换成二次函数求值域．　
[通关练习]
1．函数f(x)＝3sin在区间上的值域为(　　)
A.　　　　　　　 B.
C. D.
解析：选B.当x∈时，2x－∈，
sin∈，
故3sin∈，
即此时函数f(x)的值域是.
2．函数y＝lg sin x＋的定义域为________．
解析：要使函数有意义，则有
即
解得(k∈Z)，
所以2kπ 所以函数的定义域为.
答案：
3．函数y＝(4－3sin x)(4－3cos x)的最小值为________．
解析：y＝16－12(sin x＋cos x)＋9sin xcos x，
令t＝sin x＋cos x，则t∈[－，]，且sin xcos x＝，
所以y＝16－12t＋9×＝(9t2－24t＋23)．
故当t＝时，ymin＝.
答案：

　　　　　　三角函数的单调性(高频考点)
三角函数的单调性是每年高考命题的热点，题型既有选择题也有填空题，或解答题某一问出现，难度为中档题．
高考对三角函数单调性的考查有以下四个命题角度：
(1)求已知三角函数的单调区间；
(2)已知三角函数的单调区间求参数；
(3)利用三角函数的单调性比较大小；
(4)利用三角函数的单调性求值域(或最值)．(见本节例1(1)及通关练习T1)
[典例引领]
角度一　求已知三角函数的单调区间
(2018·沈阳市教学质量检测(一))已知f(x)＝2sin2x＋2sin xcos x，则f(x)的最小正周期和一个单调递减区间分别为(　　)
A．2π，　　　　　　 B．π，
C．2π， D．π，
【解析】　f(x)＝2sin2x＋2sin xcos x＝1－cos 2x＋sin 2x＝sin＋1，所以T＝＝π，由＋2kπ≤2x－≤＋2kπ(k∈Z)得＋kπ≤x≤＋kπ(k∈Z)，令k＝0得f(x)在上单调递减．
【答案】　B
角度二　已知三角函数的单调区间求参数
函数f(x)＝sin ωx(其中ω>0)在区间上单调递增，则ω的取值范围是________．
【解析】　因为ω>0，由2kπ－≤ωx≤2kπ＋，k∈Z，
得f(x)的增区间是，k∈Z.
因为f(x)在上单调递增，
所以⊆.
所以－≥－且≤＋，所以ω∈.
【答案】　
角度三　利用三角函数的单调性比较大小
已知函数f(x)＝2sin，设a＝f，b＝f，c＝f，则a，b，c的大小关系是(　　)
A．a C．b 【解析】　a＝f＝2sin π，b＝f＝2sin ＝2，c＝f＝2sin ＝2sin ，
因为y＝sin x在上递增，所以c 【答案】　B

(1)求三角函数单调区间的两种方法
①代换法：就是将比较复杂的三角函数含自变量的代数式整体当作一个角u(或t)，利用复合函数的单调性列不等式求解，如例2­1.
②图象法：画出三角函数的正、余弦曲线，结合图象求它的单调区间．
[提醒]　要注意求函数y＝Asin(ωx＋φ)的单调区间时ω的符号，若ω<0，那么一定先借助诱导公式将ω化为正数．同时切莫漏掉考虑函数自身的定义域．
(2)利用单调性确定ω的范围的方法
对于已知函数的单调区间的某一部分确定参数ω的范围的问题，首先，明确已知的单调区间应为函数的单调区间的子集，其次，要确定已知函数的单调区间，从而利用它们之间的关系可求解，另外，若是选择题利用特值验证排除法求解更为简捷．
(3)利用单调性比较大小的方法
首先利用诱导公式把已知角转化为同一区间内的角且函数名称相同，再利用其单调性比较大小．　
[通关练习]
1．函数f(x)＝tan的单调递增区间是(　　)
A.(k∈Z)
B.(k∈Z)
C.(k∈Z)
D.(k∈Z)
解析：选B.由kπ－<2x－ 2．(2018·浙江宁波质检)已知函数f(x)＝2sin ωx在区间上的最小值为－2，则ω的取值范围是(　　)
A.∪[6，＋∞)
B.∪
C．(－∞，－2]∪[6，＋∞)
D．(－∞，－2]∪
解析：选D.当ω>0时，由题意知－ω≤－，
即ω≥；
当ω<0时，由题意知ω≤－，所以ω≤－2.
综上可知，ω的取值范围是∪.
3．已知函数g(x)＝－cos，则g(x)的单调递增区间为________．
解析：g(x)＝－cos＝－cos，
欲求函数g(x)的单调递增区间，
只需求y＝cos的单调递减区间．
由2kπ≤2x－≤2kπ＋π，k∈Z，
得kπ＋≤x≤kπ＋，k∈Z.
故所给函数的单调递增区间为
(k∈Z)．
因为x∈，
所以函数g(x)的单调递增区间是
，.
答案：，

　　　　　　三角函数的奇偶性、周期性及对
称性(高频考点)
三角函数的奇偶性、周期性及对称性是每年高考命题的热点，题型既有选择题也有填空题，或在解答题某一问出现，难度为中档题．高考对三角函数单调性的考查有以下三个命题角度：
(1)三角函数的周期性与奇偶性；
(2)三角函数的对称轴或对称中心；
(3)三角函数的奇偶性与单调性．
[典例引领]
角度一　三角函数的周期性与奇偶性
(2018·贵阳市监测考试)下列函数中，以为最小正周期的奇函数是(　　)
A．y＝sin 2x＋cos 2x　　　　 B．y＝sin
C．y＝sin 2xcos 2x D．y＝sin22x－cos22x
【解析】　A中，y＝sin 2x＋cos 2x＝sin，为非奇非偶函数，故A错；B中，y＝sin＝cos 4x，为偶函数，故B错；C中，y＝sin 2xcos 2x＝sin 4x，最小正周期为且为奇函数，故C正确；D中，y＝sin22x－cos22x＝－cos 4x，为偶函数，故D错．
【答案】　C
角度二　三角函数的对称轴或对称中心
函数y＝sin的图象与函数y＝cos的图象(　　)
A．有相同的对称轴但无相同的对称中心
B．有相同的对称中心但无相同的对称轴
C．既有相同的对称轴也有相同的对称中心
D．既无相同的对称中心也无相同的对称轴
【解析】　由2x－＝kπ＋，k∈Z，可解得函数y＝sin的对称轴为x＝＋，k∈Z.由x－＝kπ，k∈Z，可解得函数y＝cos的对称轴为x＝kπ＋，k∈Z.当k＝0时，函数有相同的对称轴．由2x－＝kπ，k∈Z，可解得函数y＝sin的对称中心为，k∈Z.由x－＝kπ＋，k∈Z，可解得函数y＝cos的对称中心为，k∈Z.
故两个函数没有相同的对称中心，故选A.
【答案】　A
角度三　三角函数的奇偶性与单调性
(2018·广州市综合测试(一))已知函数f(x)＝sin(ωx＋φ)＋cos(ωx＋φ)(ω>0，0<φ<π)是奇函数，直线y＝与函数f(x)的图象的两个相邻交点的横坐标之差的绝对值为，则(　　)
A．f(x)在上单调递减
B．f(x)在上单调递减
C．f(x)在上单调递增
D．f(x)在上单调递增
【解析】　f(x)＝sin(ωx＋φ)＋cos(ωx＋φ)＝sin，因为0<φ<π且f(x)为奇函数，所以φ＝，即f(x)＝－sin ωx，又直线y＝与函数f(x)的图象的两个相邻交点的横坐标之差的绝对值为，所以函数f(x)的最小正周期为，由＝，可得ω＝4，故f(x)＝－sin 4x，由2kπ＋≤4x≤2kπ＋，k∈Z，即＋≤x≤＋，k∈Z，令k＝0，得≤x≤，此时f(x)在上单调递增．
【答案】　D

三角函数的奇偶性、对称性和周期问题的解题思路
(1)奇偶性的判断方法：三角函数中奇函数一般可化为y＝Asin ωx或y＝Atan ωx的形式，而偶函数一般可化为y＝Acos ωx＋b的形式．
(2)周期的计算方法：利用函数y＝Asin(ωx＋φ)(ω>0)，y＝Acos(ωx＋φ)(ω>0)的周期为，函数y＝Atan(ωx＋φ)(ω>0)的周期为求解．
(3)解决对称性问题的关键：熟练掌握三角函数的对称轴、对称中心．
[提醒]　对于函数y＝Asin(ωx＋φ)，其对称轴一定经过图象的最高点或最低点，对称中心的横坐标一定是函数的零点，因此在判断直线x＝x0或点(x0，0)是否是函数的对称轴或对称中心时，可通过检验f(x0)的值进行判断．　
[通关练习]
1．已知f(x)＝sin x＋cos x(x∈R)，函数y＝f(x＋φ)的图象关于直线x＝0对称，则φ的值为(　　)
A. B.
C. D.
解析：选D.f(x)＝2sin，
y＝f(x＋φ)＝2sin的图象关于x＝0对称，
即f(x＋φ)为偶函数．
所以＋φ＝＋kπ，k∈Z，
即φ＝kπ＋，k∈Z，
又因为|φ|≤，所以φ＝，故选D.
2．已知函数f(x)＝2sin(ω>0)的最小正周期为4π，则该函数的图象(　　)
A．关于点对称 B．关于点对称
C．关于直线x＝对称 D．关于直线x＝对称
解析：选B.函数f(x)＝2sin(ω>0)的最小正周期是4π，而T＝＝4π，所以ω＝，
即f(x)＝2sin.函数f(x)的对称轴为＋＝＋kπ，解得x＝π＋2kπ(k∈Z)；
函数f(x)的对称中心的横坐标为＋＝kπ，解得x＝2kπ－π(k∈Z)．
所以f(x)的对称中心为.
3．(2018·揭阳模拟)已知函数f(x)是周期为2的奇函数，当x∈[0，1)时，f(x)＝lg(x＋1)，则f＋lg 18＝________．
解析：因为当x∈[0，1)时，f(x)＝lg(x＋1)，
f＝lg，
又因为函数f(x)是周期为2的奇函数，
所以f＝f＝－f＝－lg，
所以f＋lg 18＝lg 18－lg＝lg 10＝1.
答案：1

奇偶性
对于y＝Asin(ωx＋φ)(A≠0)，若为奇函数，则φ＝kπ(k∈Z)；若为偶函数，则φ＝＋kπ(k∈Z)．对于y＝Acos(ωx＋φ)(A≠0)，若为奇函数，则φ＝＋kπ(k∈Z)；若为偶函数，则φ＝kπ(k∈Z)．对于y＝Atan(ωx＋φ)(A≠0)，若为奇函数，则φ＝π(k∈Z)．
函数图象的对称中心、对称轴
(1)求形如y＝Asin(ωx＋φ)或y＝Acos(ωx＋φ)的函数图象的对称轴或对称中心时，都是先把“ωx＋φ”看作一个整体，然后根据y＝sin x和y＝cos x图象的对称轴或对称中心进行求解．
(2)在判断对称轴或对称中心时，用以下结论可快速解题：设y＝f(x)＝Asin(ωx＋φ)，g(x)＝Acos(ωx＋φ)，x＝x0是对称轴方程⇔f(x0)＝±A，g(x0)＝±A；(x0，0)是对称中心⇔f(x0)＝0，g(x0)＝0.
易错防范
(1)闭区间上最值或值域问题，首先要在定义域基础上分析单调性；含参数的最值问题，要讨论参数对最值的影响．
(2)要注意求函数y＝Asin(ωx＋φ)的单调区间时A和ω的符号，尽量化成ω>0时的情况，避免出现增减区间的混淆．　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

1．f(x)＝tan x＋sin x＋1，若f(b)＝2，则f(－b)＝(　　)
A．0　　　　 B．3
C．－1 D．－2
解析：选A.因为f(b)＝tan b＋sin b＋1＝2，
即tan b＋sin b＝1.
所以f(－b)＝tan(－b)＋sin(－b)＋1
＝－(tan b＋sin b)＋1＝0.
2．(2018·南昌市第一次模拟)已知函数f(x)＝Asin(ωx＋φ)(A>0，ω>0，0<φ<)的周期为π，若f(α)＝1，则f＝(　　)
A．－2 B．－1
C．1 D．2
解析：选B.因为函数f(x)＝Asin(ωx＋φ)(A>0，ω>0，
0<φ<)的周期为π，所以T＝＝π，得ω＝2，
从而由f(α)＝1，得Asin(2α＋φ)＝1，f
＝Asin＝Asin
＝－Asin(2α＋φ)＝－1.
3．最小正周期为π且图象关于直线x＝对称的函数是(　　)
A．y＝2sin B．y＝2sin
C．y＝2sin D．y＝2sin
解析：选B.由函数的最小正周期为π，可排除C.由函数图象关于直线x＝对称知，该直线过函数图象的最高点或最低点，对于A，因为sin＝sin π＝0，所以选项A不正确．对于D，sin＝sin＝，所以D不正确，对于B，sin＝sin＝1，所以选项B正确，故选B.
4．(2017·高考全国卷Ⅲ)函数f(x)＝sin(x＋)＋cos(x－)的最大值为(　　)
A. B．1
C. D.
解析：选A.因为cos(x－)＝cos[(x＋)－]＝sin(x＋)，所以f(x)＝sin(x＋)，于是f(x)的最大值为，故选A.
5．(2018·石家庄教学质量检测(二))已知函数f(x)＝sin，f′(x)是f(x)的导函数，则函数y＝2f(x)＋f′(x)的一个单调递减区间是(　　)
A. B.
C. D.
解析：选A.由题意，得f′(x)＝2cos，所以y＝2f(x)＋f′(x)＝2sin＋2cos＝2sin＝2sin.由2kπ＋≤2x＋≤2kπ＋(k∈Z)，得kπ＋≤x≤kπ＋(k∈Z)，所以y＝2f(x)＋f′(x)的一个单调递减区间为，故选A.
6．比较大小：sin________sin.
解析：因为y＝sin x在上为增函数且－＞－，故sin＞sin.
答案：＞
7．若函数f(x)＝2cos的最小正周期为T，T∈(1，3)，则正整数ω的最大值为________．
解析：因为T＝，T∈(1，3)，
所以1<<3，即<ω<2π.
所以正整数ω的最大值为6.
答案：6
8．已知f(x)＝sin 2x－cos 2x，若对任意实数x∈，都有|f(x)| 解析：因为f(x)＝sin 2x－cos 2x＝2sin，x∈，所以∈，
所以2sin∈(－，1]，
所以|f(x)|＝|2sin<，所以m≥.
答案：[，＋∞)
9．(2017·高考北京卷)已知函数f(x)＝cos－2sin xcos x.
(1)求f(x)的最小正周期；
(2)求证：当x∈时，f(x)≥－.
解：(1)f(x)＝cos 2x＋sin 2x－sin 2x
＝sin 2x＋cos 2x
＝sin(2x＋)．
所以f(x)的最小正周期T＝＝π.
(2)证明：因为－≤x≤，
所以－≤2x＋≤.
所以sin(2x＋)≥sin(－)＝－.
所以当x∈[－，]时，f(x)≥－.
10．(2018·合肥市第二次教学质量检测)已知函数f(x)＝sin ωx－cos ωx(ω>0)的最小正周期为π.
(1)求函数y＝f(x)图象的对称轴方程；
(2)讨论函数f(x)在上的单调性．
解：(1)因为f(x)＝sin ωx－cos ωx＝sin，且T＝π，所以ω＝2.于是，f(x)＝sin.令2x－＝kπ＋(k∈Z)，得x＝＋(k∈Z)，即函数f(x)图象的对称轴方程为x＝＋(k∈Z)．
(2)令2kπ－≤2x－≤2kπ＋(k∈Z)，得函数f(x)的单调递增区间为(k∈Z)．注意到x∈，所以令k＝0，得函数f(x)在上的单调递增区间为；同理，其单调递减区间为.

1．已知函数f(x)＝，则下列说法正确的是(　　)
A．f(x)的周期是
B．f(x)的值域是{y|y∈R，且y≠0}
C．直线x＝是函数f(x)图象的一条对称轴
D．f(x)的单调递减区间是，k∈Z
解析：选D.函数f(x)＝的周期为T＝＝2π，故A错误；函数f(x)＝的值域为[0，＋∞)，故B错误；当x＝时，x－＝≠，k∈Z，
即x＝不是f(x)的对称轴，故C错误；
令kπ－ 解得x∈，k∈Z，
所以函数f(x)的单调减区间为，k∈Z，故D正确．
2．(2018·武汉市武昌区调研考试)若f(x)＝cos 2x＋acos 在区间上是增函数，则实数a的取值范围为(　　)
A．[－2，＋∞) B．(－2，＋∞)
C．(－∞，－4) D．(－∞，－4]
解析：选D.f(x)＝1－2sin2x－asin x，令sin x＝t，t∈，则g(t)＝－2t2－at＋1，t∈，因为f(x)在上单调递增，所以－≥1，即a≤－4，故选D.
3．已知函数f(x)＝sin(ω>0)，x∈R.若函数f(x)在区间(－ω，ω)内单调递增，且函数y＝f(x)的图象关于直线x＝ω对称，则ω的值为(　　)
A. B．2
C. D.
解析：选D.因为f(x)在区间(－ω，ω)内单调递增，且函数图象关于直线x＝ω对称，所以f(ω)必为一个周期上的最大值，
所以有ω·ω＋＝2kπ＋，k∈Z，
所以ω2＝＋2kπ，k∈Z，又ω－(－ω)≤·，ω>0，
即ω2≤，即ω2＝，所以ω＝.
4．(2018·湖南省湘中名校联考)已知函数f(x)＝sin(2x＋φ)，其中φ为实数，若f(x)≤对x∈R恒成立，且f>f(π)，则f(x)的单调递增区间是(　　)
A.(k∈Z)
B.(k∈Z)
C.(k∈Z)
D.(k∈Z)
解析：选C.因为f(x)≤对x∈R恒成立，即＝＝1，所以φ＝kπ＋(k∈Z)．因为f>f(π)，所以sin(π＋φ)>sin(2π＋φ)，
即sin φ<0，所以φ＝－π＋2kπ(k∈Z)，所以f(x)＝sin(2x－π)，所以由三角函数的单调性知2x－∈[2kπ－，2kπ＋](k∈Z)，得x∈[kπ＋，kπ＋](k∈Z)即为f(x)的单调递增区间，故选C.
5．已知f(x)＝sin.
(1)求函数f(x)图象的对称轴方程；
(2)求f(x)的单调递增区间；
(3)当x∈时，求函数f(x)的最大值和最小值．
解：(1)f(x)＝sin，
令2x＋＝kπ＋，k∈Z，则x＝＋，k∈Z.
所以函数f(x)图象的对称轴方程是x＝＋，k∈Z.
(2)令2kπ－≤2x＋≤2kπ＋，k∈Z，
则kπ－≤x≤kπ＋，k∈Z.
故f(x)的单调递增区间为，k∈Z.
(3)当x∈时，≤2x＋≤，
所以－1≤sin≤，所以－≤f(x)≤1，所以当x∈时，函数f(x)的最大值为1，最小值为－.
6．已知a>0，函数f(x)＝－2asin＋2a＋b，当x∈时，－5≤f(x)≤1.
(1)求常数a，b的值；
(2)设g(x)＝f且lg g(x)>0，求g(x)的单调区间．
解：(1)因为x∈，所以2x＋∈.
所以sin∈，
所以－2asin∈[－2a，a]．
所以f(x)∈[b，3a＋b]，
又因为－5≤f(x)≤1，
所以b＝－5，3a＋b＝1，因此a＝2，b＝－5.
(2)由(1)得，
f(x)＝－4sin－1，
g(x)＝f＝－4sin－1
＝4sin－1，
又由lg g(x)>0，得g(x)>1，
所以4sin－1>1，所以sin>，
所以2kπ＋<2x＋<2kπ＋，k∈Z，
其中当2kπ＋<2x＋≤2kπ＋，k∈Z时，g(x)单调递增，即kπ 所以g(x)的单调增区间为，k∈Z.
又因为当2kπ＋<2x＋<2kπ＋，k∈Z时，
g(x)单调递减，即kπ＋ 所以g(x)的单调减区间为，k∈Z.