初中数学第二章 相交线与平行线2 探索直线平行的条件教学演示ppt课件

这是一份初中数学第二章 相交线与平行线2 探索直线平行的条件教学演示ppt课件，共18页。PPT课件主要包含了学习目标，导入新课，回顾与思考，①在直线EF的两侧，∠4和∠6，内错角，讲授新课，①在直线EF的同旁，∠3和∠6，同旁内角等内容，欢迎下载使用。
1.理解内错角、同旁内角的概念；2.结合图形识别内错角、同旁内角；（重点）3.会运用内错角、同旁内角判定两条直线平行.（难点）
问题 上节课你学了平行线的哪些内容？
2.如果两条直线都与第三条直线平行，那么这两条直线互相平行.
1.经过直线外一点，有且只有一条直线与已知直线平行.
3.同位角相等，两直线平行.
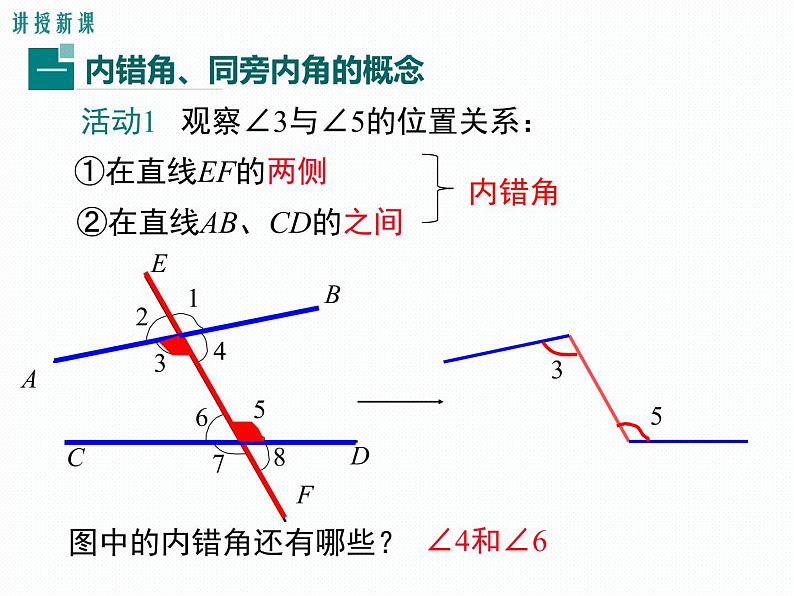
活动1 观察∠3与∠5的位置关系：
②在直线AB、CD的之间
图中的内错角还有哪些？
变式图形：图中的∠1与∠2都是内错角.
图形特征：在形如“Z”的图形中有内错角.
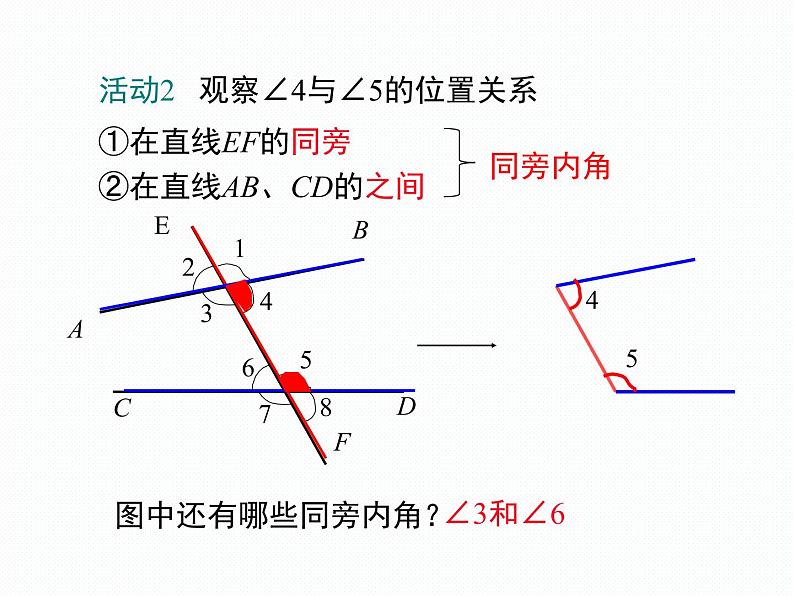
活动2 观察∠4与∠5的位置关系
图中还有哪些同旁内角？
变式图形：图中的∠1与∠2都是同旁内角.
图形特征：在形如“U”的图形中有同旁内角.　
例1 如图，直线DE截AB ，AC，构成8个角，指出所有的同位角,内错角,同旁内角.
解：同位角：∠2与∠5，∠4与∠7，∠1与∠8, ∠6和∠3；内错角：∠4与∠5，∠1与∠6；同旁内角：∠1与∠5，∠4与∠6.
变式：∠A与∠8是哪两条直线被第哪条直线所截的角?它们是什么关系的角?∠A与∠5呢?∠A与∠6呢?
例2 如图，直线DE,BC被直线AB所截. （1）∠1与∠2， ∠1和∠3，∠1和∠4各是什么角？
解：∠1与∠2是内错角， ∠1和∠3同旁内角， ∠1和∠4是同位角.
注意：解题之前要明确哪两条直线被哪条直线所截.
解：∵∠1=∠4（已知）， 又∵∠2=∠4（对顶角相等）， ∴∠1=∠2（等量代换）. ∵∠3+∠4=180°， 又∵∠1=∠4（已知）， ∴∠1+∠3=180°（等量代换）， 即∠1与∠3互补.
（2）如果∠1=∠4，那么∠1与∠2相等吗？∠1与∠3互补吗?为什么？
问题1 两条直线被第三条直线所截，同时得到同位角、内错角和同旁内角，由同位角相等可以判定两直线平行，那么，能否利用内错角和同旁内角来判定两直线平行呢？
如图，由3=2，可推出a//b吗？如何推出？
解： ∵ 3=2(已知）， 3=1（对顶角相等），  1= 2.  a//b(同位角相等，两直线平行）.
判定方法2：两条直线被第三条直线所截 ,如果内错 角相等,那么这两条直线平行.
简单说成：内错角相等，两直线平行.
∵∠3=∠2(已知)∴a∥b（内错角相等，两直线平行）
问题2 如图，如果1+2=180° ，你能判定a//b吗?
解:能, ∵1+2=180°（已知） 1+3=180°（邻补角定义）2=3（同角的补角相等）a//b（同位角相等，两直线平行）
判定方法3：两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行.
简单说成：同旁内角互补，两直线平行.
∵∠1+∠2=180°(已知)∴a∥b（内错角相等，两直线平行）
1.如图，∠1=30°∠2或∠3满足条件 __________________，则a//b.
∠2＝150°或∠3＝30°
2.如图.（1）从∠1=∠4，可以推出　 ∥ ， 理由是 .
内错角相等，两直线平行
（2）从∠ABC +∠ =180°，可以推出AB∥CD ，理由是 .
同旁内角互补,两直线平行
3.如图，已知∠1= ∠3，AC平分∠DAB你能判断那两条直线平行？请说明理由？
理由： ∵AC平分∠DAB（已知） ∴∠1=∠2（角平分线定义） 又∵∠1=∠3（已知） ∴∠2=∠3（等量代换） ∴AB∥CD( 内错角相等，两直线平行)
1.同位角、内错角、同旁内角的结构特征:
同位角 “F”型
内错角 “Z”型
同旁内角 “U”型