2020届高考数学一轮复习课时训练：第3章 导数及其应用 14-3(含解析)

【课时训练】课时3　导数与函数的综合问题

一、选择题

1.(2018海南中学模拟)设f(x)是定义在R上的奇函数，且f(2)=0，当x>0时，有<0恒成立，则不等式x2f(x)>0的解集是(　　)

A.(－2,0)∪(2，＋∞)　 B.(－2,0)∪(0,2)

C.(－∞，－2)∪(2，＋∞)　 D.(－∞，－2)∪(0,2)

答案为：D

解析：∵当x>0时，=′<0，∴φ(x)=在(0，＋∞)为减函数，

又f(x)是定义在R上的奇函数，∴f(x)在R上单调递增.

∵f(2)=0，∴在(0,2)内恒有f(x)>0；在(2，＋∞)内恒有f(x)<0.

故在(－∞，－2)内恒有f(x)>0；在(－2,0)内恒有f(x)<0.

故x2f(x)>0的解集为(－∞，－2)∪(0,2).

2.(2018河北故城模拟)若关于x的不等式x3－3x2－9x＋2≥m对任意x∈[－2,2]恒成立，则m的取值范围是(　　)

A.(－∞，7]　 B.(－∞，－20]　　

C.(－∞，0] D.[－12,7]

答案为：B

解析：令f(x)=x3－3x2－9x＋2，则f ′(x)=3x2－6x－9，

令f ′(x)=0得x=－1或x=3(舍去).

∵f(－1)=7, f(－2)=0, f(2)=－20，

∴f(x)的最小值为f(2)=－20，故m≤－20.

3.(2018贵阳联考)已知函数f(x)的定义域为[－1,4]，部分对应值如下表：

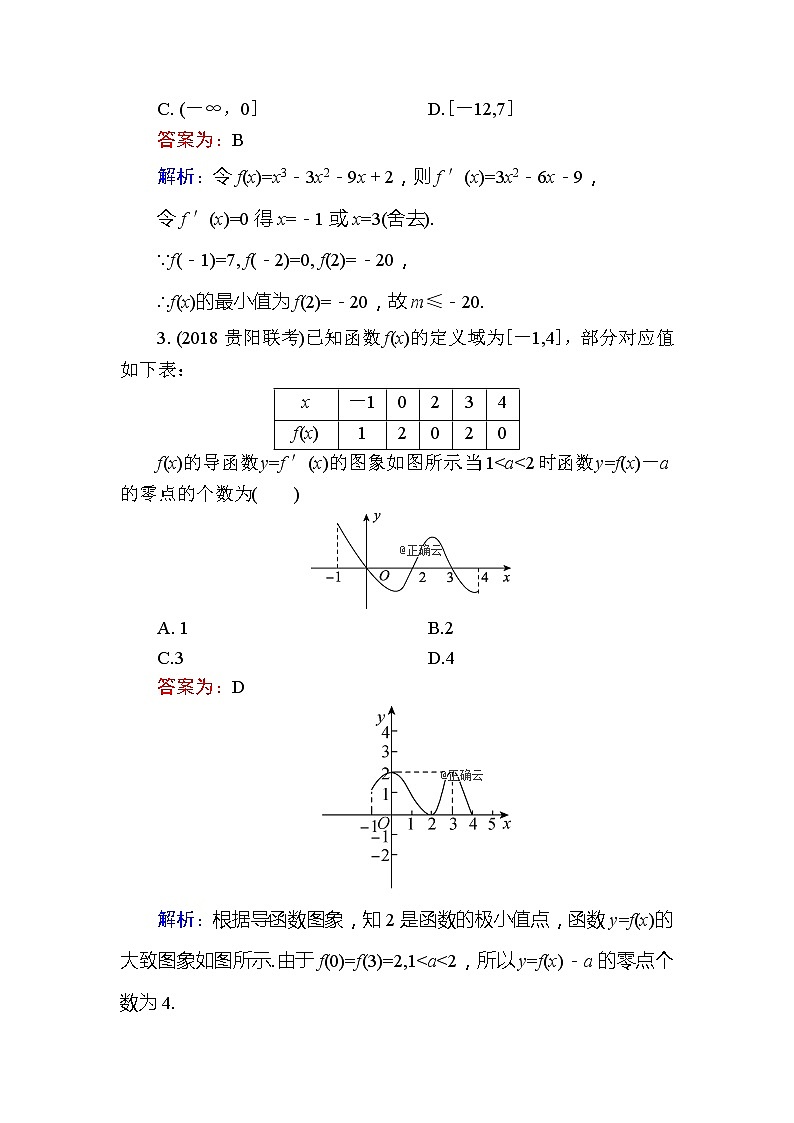
f(x)的导函数y=f ′(x)的图象如图所示.当1<a<2时，函数y=f(x)－a的零点的个数为(　　)

A.1 B.2

C.3 D.4

答案为：D

解析：根据导函数图象，知2是函数的极小值点，函数y=f(x)的大致图象如图所示.由于f(0)=f(3)=2,1<a<2，所以y=f(x)－a的零点个数为4.

4.(2018河南濮阳一模)函数f(x)的导函数为f ′(x)，若∀x∈R恒有f ′(x)<f(x)成立，且f(2)=1，则不等式f(x)>ex－2的解集为(　　)

A.(－∞，1) B.(1，＋∞)

C.(2，＋∞) D.(－∞，2)

答案为：D

解析：设函数g(x)=，则g′(x)=<0，

∴g(x)在R上单调递减，不等式f(x)>ex－2可转化为>.∵g(2)==，∴>，∴x＜2，∴x∈(－∞，2).故选D.

二、填空题

5.(2018大连模拟)函数y=x＋2cos x在区间上的最大值是________.

答案为：＋

解析：y′=1－2sin x，令y′=0，又x∈，得x=，则x∈时，y′>0；x∈时，y′<0.故函数y=x＋2cos x在上单调递增，在上单调递减，所以当x=时，函数取得最大值＋.

6.(2018安徽江南名校联考)已知x∈(0,2)，若关于x的不等式<恒成立，则实数k的取值范围为________.

答案为：[0，e－1)

解析：依题意，知k＋2x－x2>0，即k>x2－2x对任意x∈(0,2)恒成立，从而k≥0，

因此由原不等式，得k<＋x2－2x恒成立.

令f(x)=＋x2－2x，则f ′(x)=(x－1).

令f ′(x)=0，得x=1，当x∈(1,2)时， f ′(x)>0，函数f(x)在(1,2)上单调递增；当x∈(0,1)时， f ′(x)<0，函数f(x)在(0,1)上单调递减.所以k<f(x)min=f(1)=e－1，

故实数k的取值范围是[0，e－1).

三、解答题

7.(2018云南大理二模)设f(x)=(x＋1)eax(其中a≠0)，曲线y=f(x)在x=处有水平切线.

(1)求a的值；

(2)设g(x)=f(x)＋x＋xln x，证明：对任意x1，x2∈(0,1)有|g(x1)－g(x2)|＜e－1＋2e－2.

(1)【解】f ′(x)=eax＋a(x＋1)eax=(ax＋a＋1)eax.

由题意知0=f ′=(a＋2)e，解得a=－2.

(2)【证明】令g(x)=g1(x)＋g2(x)，x∈(0,1)，其中g1(x)=(x＋1)e－2x＋x，g2(x)=xln x，求导得g1′(x)=－(2x＋1)e－2x＋1.对h(x)=g1′(x)求导得h′(x)=－2e－2x＋2(2x＋1)e－2x=4xe－2x＞0，x∈(0,1).

因此g1′(x)在(0,1)上为增函数，故当x∈(0,1)时，g1′(x)＞g1′(0)=0.因此g1(x)在(0,1)上也为增函数，从而1=g1(0)＜g1(x)＜g1(1)=1＋2e－2(0＜x＜1).①

又g2′(x)=1＋ln x，令g2′(x)=0，解得x=e－1.当0＜x＜e－1时，g2′(x)＜0，g2(x)在(0，e－1)上为减函数；当e－1＜x＜1时，g2′(x)＞0，g2(x)在(e－1,1)上为增函数，从而g2(x)在(0,1)上取得的最小值为g2(e－1)=－e－1，因此－e－1≤g2(x)＜0(0＜x＜1).②

由①②得1－e－1＜g(x)＜1＋2e－2(0＜x＜1)，因此对任意x1，x2∈(0,1)，有|g(x1)－g(x2)|＜(1＋2e－2)－(1－e－1)=e－1＋2e－2.

8.(2019贵阳检测)已知函数f(x)=(x－1)ex＋1，x∈[0,1].　

(1)证明：f(x)≥0；

(2)若a<<b对任意的x∈(0,1)恒成立，求b－a的最小值.

(1)【证明】因为f ′(x)=xex≥0，即f(x)在[0,1]上单调递增，

所以f(x)≥f(0)=0，即结论成立.

(2)【解】令g(x)=，则g ′(x)=>0，x∈(0,1)，

所以当x∈(0,1)时，g(x)<g(1)=e－1，

要使<b，只需b≥e－1.

要使>a成立，只需ex－ax－1>0在x∈(0,1)恒成立，

令h(x)=ex－ax－1，x∈(0,1)，则h ′(x)=ex－a.

由x∈(0,1)，得ex∈(1，e).

①当a≤1时，h ′(x)>0，此时x∈(0,1)，有h(x)>h(0)=0成立，所以a≤1满足条件；

②当a≥e时，h′(x)<0，此时x∈(0,1)，有h(x)<h(0)=0，不符合题意，舍去；

③当1<a<e时，令h′(x)=0，得x=ln a.当x∈(0，ln a)时，h′(x)<0，即x∈(0，ln a)时，h(x)<h(0)=0，不符合题意，舍去.

综上，a≤1.又b≥e－1，所以b－a的最小值为e－2.

9.(2018沈阳监测)已知函数f(x)=aln x(a＞0)，e为自然对数的底数.

(1)若过点A(2，f(2))的切线斜率为2，求实数a的值；

(2)当x＞0时，求证：f(x)≥a；

(3)若在区间(1，e)上e－ex＜0恒成立，求实数a的取值范围.

(1)【解】由题意得f ′(x)=，∴f ′(2)==2，∴a=4.

(2)【证明】f(x)≥a等价于a≥0，

令g(x)=a(ln x－1＋)，则g′(x)=a.

令g′(x)=0，即a=0，解得x=1，

∴g(x)在(0,1)上单调递减，在(1，＋∞)上单调递增.

∴g(x)的最小值为g(1)=0，∴f(x)≥a.

(3)【解】由题意可知答案为：e＜ex，化简得＜ln x，

又x∈(1，e)，∴a＞.

令h(x)=，则h′(x)==，　

由(2)知，当x∈(1，e)时，ln x－1＋＞0，

∴h′(x)＞0，即h(x)在(1，e)上单调递增，

∴h(x)＜h(e)=e－1.∴a≥e－1.