2020届高考数学一轮复习课时训练：第3章 导数及其应用 14-2(含解析)

【课时训练】课时2　导数与函数的极值、最值

一、选择题

1.(2018山东菏泽一模)函数f(x)=ln x－x在区间(0，e]上的最大值为(　　)

A.1－e B.－1　

C.－e D.0

答案为：B

解析：因为f ′(x)=－1=，当x∈(0,1)时， f ′(x)＞0；当x∈(1，e]时， f ′(x)＜0，所以f(x)的单调递增区间是(0,1)，单调递减区间是(1，e]，所以当x=1时， f(x)取得最大值ln 1－1=－1.

2.(2018广西来宾一模)已知函数f(x)=x(x－m)2在x=1处取得极小值，则实数m=(　　)

A.0　 B.1　　

C.2 D.3

答案为：B

解析：f ′(x)=(x－m)2＋2x(x－m)=(x－m)·(3x－m).由f ′(1)=0可得m=1或m=3.当m=3时， f ′(x)=3(x－1)(x－3)，当1＜x＜3时， f ′(x)＜0；当x＜1或x＞3时， f ′(x)＞0.此时在x=1处取得极大值，不合题意.所以m=1，此时f ′(x)=(x－1)(3x－1)，当＜x＜1时， f ′(x)＜0；当x＜或x＞1时， f ′(x)＞0.此时在x=1处取得极小值.选B.

3.(2018安徽池州一模)已知函数f(x)=x3－px2－qx的图象与x轴切于点(1,0)，则f(x)的极大值、极小值分别为(　　)

A.－，0　　 B.0，－

C.，0  D.0，

答案为：C

解析：由题意知， f ′(x)=3x2－2px－q，由f ′(1)=0, f(1)=0得解得p=2，q=－1，∴f(x)=x3－2x2＋x.由f ′(x)=3x2－4x＋1=0，得x=或x=1，易知当x=时， f(x)取极大值，当x=1时， f(x)取极小值0.

4.(2018山东潍坊二模)已知函数f(x)=x3＋3x2－9x＋1，若f(x)在区间[k,2]上的最大值为28，则实数k的取值范围为(　　)

A.[－3，＋∞)　 B.(－3，＋∞)

C.(－∞，－3)  D.(－∞，－3]

答案为：D

解析：由题意知f ′(x)=3x2＋6x－9，令f ′(x)=0，解得x=1或x=－3，所以f ′(x), f(x)随x的变化情况如下表：

又f(－3)=28, f(1)=－4, f(2)=3, f(x)在区间[k,2]上的最大值为28，所以k≤－3.

5.(2018长沙模拟)已知函数f(x)=(a＞0)在[1，＋∞)上的最大值为，则a的值为(　　)

A.－1　 B.

C. D.＋1

答案为：A

解析：由f(x)=得f ′(x)=.当a＞1时，若x＞，则f ′(x)＜0, f(x)单调递减；若1＜x＜，则f ′(x)＞0, f(x)单调递增.故当x=时，函数f(x)有最大值=，得a=＜1，不合题意；当a=1时，函数f(x)在[1，＋∞)上单调递减，最大值为f(1)=，不合题意；当0＜a＜1时，函数f(x)在[1，＋∞)上单调递减，此时最大值为f(1)==，得a=－1，符合题意，故a的值为－1.选A.

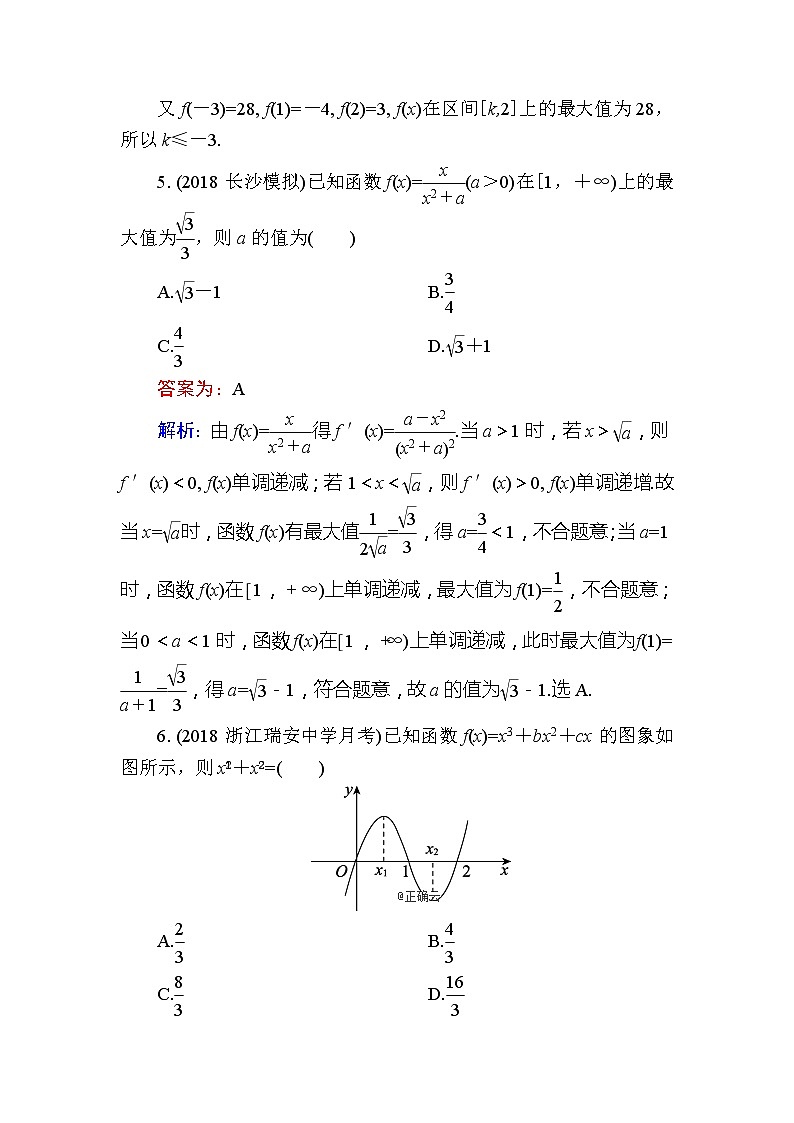
6.(2018浙江瑞安中学月考)已知函数f(x)=x3＋bx2＋cx的图象如图所示，则x＋x=(　　)

A.　 B.

C. D.

答案为：C

解析：由图象可知f(x)的图象过点(1,0)与(2,0)，因此解得b=－3，c=2，所以f(x)=x3－3x2＋2x，所以f ′(x)=3x2－6x＋2.因为x1，x2是方程f ′(x)=3x2－6x＋2=0的两根，所以x1＋x2=2，x1x2=，所以x＋x=(x1＋x2)2－2x1x2=4－=.

7.(2018福建宁德一模)若函数f(x)=x3＋x2－在区间(a，a＋5)上存在最小值，则实数a的取值范围是(　　)

A.[－5,0)　　 B.(－5,0)　

C.[－3,0) D.(－3,0)

答案为：C

解析：由题意知， f ′(x)=x2＋2x=x(x＋2)，令f ′(x)=0，解得x=0或－2，故f(x)在(－∞，－2)，(0，＋∞)上是增函数，在(－2,0)上是减函数，做出其图象如图所示.令x3＋x2－=－得，x=0或x=－3，则结合图象可知，解得 a∈[－3,0).故选C.

8.(2018湖北武汉一模)已知函数f(x)=x3－2x2－4x－7，其导函数为f ′(x)，给出以下命题：

①f(x)的单调递减区间是；

②f(x)的极小值是－15；

③当a＞2时，对任意的x＞2且x≠a，恒有f(x)＞f(a)＋f ′(a)(x－a)；

④函数f(x)有且只有一个零点.

其中真命题的个数为(　　)

A.1　　 B.2　　

C.3 D.4

答案为：C

解析：f ′(x)=3x2－4x－4=(x－2)(3x＋2).①令f ′(x)＜0，得－＜x＜2，所以f(x)的单调递减区间是；②令f ′(x)＞0，得x＜－或x＞2，结合①可知f(x)的极小值是f(2)=－15；③显然当a＞2时，对任意的x＞2且x≠a，恒有f(x)＞f(a)＋f ′(a)(x－a)不成立；④f=－＜0, f(2)=－15＜0，并结合①②易知f(x)有且只有一个零点.故选C.

二、填空题

9.(2019江苏泰州调研)函数f(x)=x3＋x2－3x－4在[0,2]上的最小值是________.

答案为：－

解析：f′(x)=x2＋2x－3，令f′(x)=0得x=1(x=－3舍去).又f(0)=－4, f(1)=－， f(2)=－，故f(x)在[0,2]上的最小值是f(1)=－.

10.(2018广州模拟)已知函数f(x)=x3＋3ax2＋bx＋a2在x=－1时有极值0，则a－b=________.

答案为：－7

解析：由题意得f ′(x)=3x2＋6ax＋b，则解得或经检验当a=1，b=3时，函数f(x)单调递增无法取得极值，而a=2，b=9满足题意，故a－b=－7.

11.(2018广西柳州模拟)已知函数f(x)=x3＋mx2＋(m＋6)x＋1既存在极大值又存在极小值，则实数m的取值范围是________.

答案为：(－∞，－3)∪(6，＋∞)

解析：对函数f(x)求导得f ′(x)=3x2＋2mx＋m＋6，要使函数f(x)既存在极大值又存在极小值，则f ′(x)=0有两个不同的根，所以判别式Δ＞0，即4m2－12(m＋6)＞0，所以m2－3m－18＞0，解得m＞6或m＜－3.

12.(2018内蒙古包头联考)已知函数f(x)=x3－6x2＋9x－abc，a＜b＜c，且f(a)=f(b)=f(c)=0.现给出如下结论：

①f(0)f(1)＞0；　　②f(0)f(1)＜0；

③f(0)f(3)＞0；　　④f(0)f(3)＜0.

其中正确结论的序号是________.

答案为：②③

解析：∵f ′(x)=3x2－12x＋9=3(x－1)·(x－3)，由f ′(x)＜0，得1＜x＜3；由f ′(x)＞0，得x＜1或x＞3.

∴f(x)在区间(1,3)上是减函数，在区间(－∞，1)，(3，＋∞)上是增函数.

又a＜b＜c, f(a)=f(b)=f(c)=0，　

∴y极大值=f(1)=4－abc＞0，y极小值=f(3)=－abc＜0，

∴0＜abc＜4.

∴a，b，c均大于零，或者a＜0，b＜0，c＞0.

又x=1，x=3为函数f(x)的极值点，∴a<0，b<0，c>0不成立，如图.

∴f(0)＜0.∴f(0)f(1)＜0, f(0)f(3)＞0，∴正确结论的序号是②③.

三、解答题

13.(2018大连双基测试)已知函数f(x)=－ex(a＞0).

(1)求函数f(x)的单调区间；

(2)求函数f(x)在[1,2]上的最大值.

【解】(1)f(x)=－ex(a＞0)，则f ′(x)=－ex.

令f ′(x)－ex=0，则x=ln .

当x变化时， f ′(x), f(x)的变化情况如下表：

故函数f(x)的单调递增区间为；单调递减区间为.

(2)当ln≥2，即0＜a≤时， f(x)max=f(2)=－e2；

当1＜ln＜2，即＜a＜时，f(x)max=f=ln－；

当ln≤1，即a≥时，f(x)max=f(1)=－e.