2020届高考数学一轮复习：课时作业48《利用向量求空间角》(含解析) 练习

课时作业48　利用向量求空间角

1．在正方体ABCD-A1B1C1D1中，点E为BB1的中点，则平面A1ED与平面ABCD所成的锐二面角的余弦值为(　B　)

A.   B.

C.   D.

解析：以A为原点，AB，AD，AA1所在直线分别为x轴，y轴，z轴建立如图所示的空间直角坐标系A-xyz，

设棱长为1，则A1(0,0,1)，E，D(0,1,0)，

∴＝(0,1，－1)，＝，

设平面A1ED的一个法向量为n1＝(1，y，z)．

则有即∴

∴n1＝(1,2,2)．

∵平面ABCD的一个法向量为n2＝(0,0,1)，∴cos〈n1，n2〉＝＝，即所成的锐二面角的余弦值为.

2．(2019·大同模拟)设正方体ABCD-A1B1C1D1的棱长为2，则点D1到平面A1BD的距离是(　D　)

A.   B.

C.   D.

解析：如图，以点D为坐标原点，DA，DC，DD1所在直线分别为x轴，y轴，z轴，建立坐标系，

则D(0,0,0)，D1(0,0,2)，A1(2,0,2)，B(2,2,0)，＝(2,0,0)，＝(2,2,0)，＝(2,0,2)，

设平面A1BD的一个法向量n＝(x，y，z)，

则∴

令z＝1，得n＝(－1,1,1)．

∴D1到平面A1BD的距离d＝＝＝.

3．(2018·全国卷Ⅰ)已知正方体的棱长为1，每条棱所在直线与平面α所成的角都相等，则α截此正方体所得截面面积的最大值为(　A　)

A.   B.

C.   D.

解析：由正方体的性质及题意可得，正方体共顶点的三条棱所在直线与平面α所成的角均相等．

如图，正方体ABCD-A1B1C1D1中，

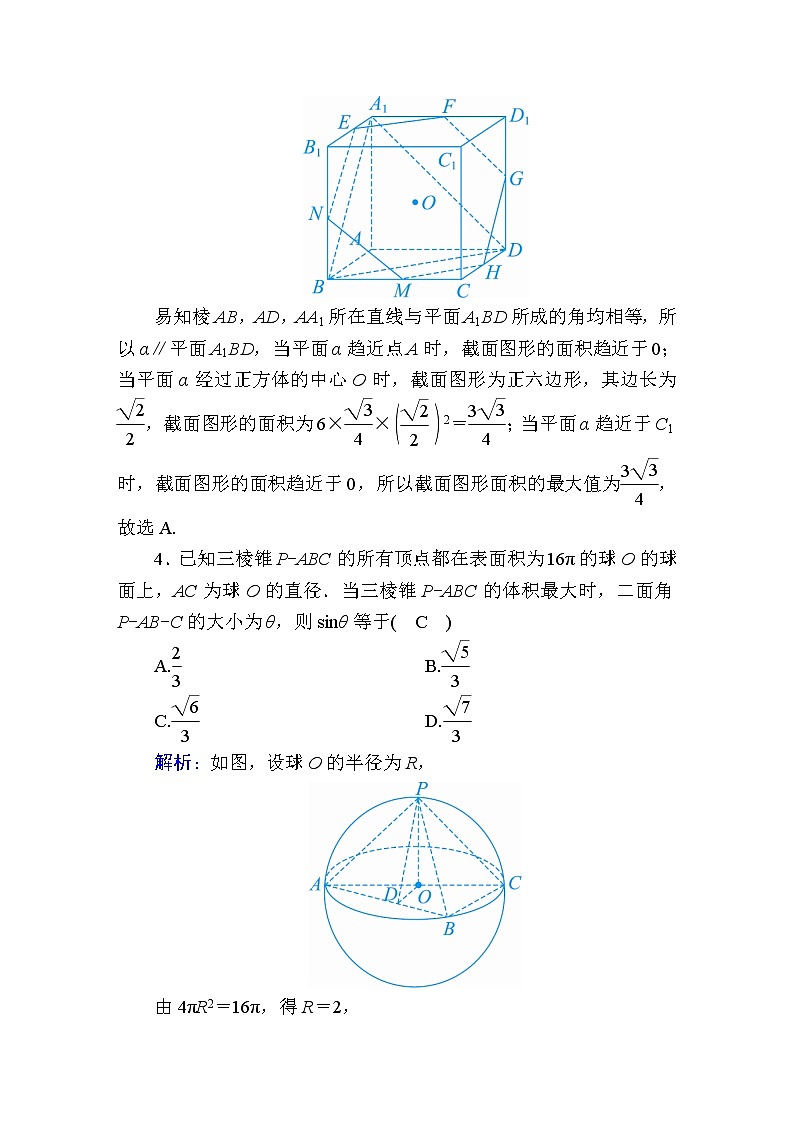
易知棱AB，AD，AA1所在直线与平面A1BD所成的角均相等，所以α∥平面A1BD，当平面α趋近点A时，截面图形的面积趋近于0；当平面α经过正方体的中心O时，截面图形为正六边形，其边长为，截面图形的面积为6××2＝；当平面α趋近于C1时，截面图形的面积趋近于0，所以截面图形面积的最大值为，故选A.

4．已知三棱锥P-ABC的所有顶点都在表面积为16π的球O的球面上，AC为球O的直径．当三棱锥P-ABC的体积最大时，二面角P-AB-C的大小为θ，则sinθ等于(　C　)

A.   B.

C.  D.

解析：如图，设球O的半径为R，

由4πR2＝16π，得R＝2，

设点P到平面ABC的距离为d，

则0＜d≤2，因为AC为球的直径，

所以AB2＋BC2＝AC2＝16，则

V三棱锥P-ABC＝AB·BC·d≤··2＝，

当且仅当AB＝BC＝2，d＝2时，V三棱锥P-ABC取得最大值，

此时平面PAC⊥平面ABC，

连接PO，因为PO⊥AC，平面PAC∩平面ABC＝AC，PO⊂平面PAC，

所以PO⊥平面ABC，过点P作PD⊥AB于D，

连接OD，因为AB⊥PO，AB⊥PD，PO∩PD＝P，

所以AB⊥平面POD，则AB⊥OD，

所以∠PDO为二面角P-AB-C的平面角，

因为OD＝BC＝，所以PD＝＝，

则sinθ＝sin∠PDO＝＝，故选C.

5．如图所示，在正方体ABCD-A1B1C1D1中，E，F分别是正方形A1B1C1D1和正方形ADD1A1的中心，则EF和CD所成的角的大小是　45°　.

解析：以D为原点，分别以DA、DC、DD1所在直线为x轴、y轴、z轴建立如图所示的空间直角坐标系D-xyz，

设正方体的棱长为1，则D(0,0,0)，C(0,1,0)，E，F，＝，＝(0,1,0)，

∴cos〈，〉＝＝－，∴〈，〉＝135°，

∴异面直线EF和CD所成的角的大小是45°.

6．如图，四边形ABCD和ADPQ均为正方形，它们所在的平面互相垂直，动点M在线段PQ上，E，F分别为AB，BC的中点．设异面直线EM与AF所成的角为θ，则cosθ的最大值为　　.

解析：建立空间直角坐标系如图所示．

设AB＝1，则＝，E.

设M(0，y,1)(0≤y≤1)，则＝.

∵θ∈，∴cosθ＝

＝＝.

则2＝1－.

令8y＋1＝t，1≤t≤9，

则＝≥，

当且仅当t＝1时取等号．

∴cosθ＝≤×＝，当且仅当y＝0时取等号．

7．如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点．

(1)证明：PB∥平面AEC；

(2)设二面角D-AE-C为60°，AP＝1，AD＝，求三棱锥E-ACD的体积．

解：(1)证明：连接BD交AC于点O，连接EO.

因为ABCD为矩形，所以O为BD的中点．

又E为PD的中点，所以EO∥PB.

又因为EO⊂平面AEC，PB⊄平面AEC，所以PB∥平面AEC.

(2)因为PA⊥平面ABCD，ABCD为矩形，所以AB，AD，AP两两垂直．

如图，以A为坐标原点，的方向为x轴的正方向，||为单位长，建立空间直角坐标系A-xyz，

则D(0，，0)，E，＝.

设B(m,0,0)(m＞0)，

则C(m，，0)，＝(m，，0)．

设n1＝(x，y，z)为平面ACE的法向量，

则即

可取n1＝.

又n2＝(1,0,0)为平面DAE的法向量，

由题设得|cos〈n1，n2〉|＝，

即 ＝，解得m＝.

因为E为PD的中点，

所以三棱锥E-ACD的高为.

三棱锥E-ACD的体积V＝××××＝.

8．(2019·江西六校联考)在如图所示的几何体中，四边形ABCD为平行四边形，∠ABD＝90°，EB⊥平面ABCD，EF∥AB，AB＝2，EB＝，EF＝1，BC＝，且M是BD的中点．

(1)求证：EM∥平面ADF；

(2)求二面角A-FD-B的余弦值的大小．

解：(1)证法一：取AD的中点N，连接MN，NF.

在△DAB中，M是BD的中点，N是AD的中点，所以MN∥AB，MN＝AB，

又因为EF∥AB，EF＝AB，

所以MN∥EF且MN＝EF.

所以四边形MNFE为平行四边形，所以EM∥FN，

又因为FN⊂平面ADF，EM⊄平面ADF，故EM∥平面ADF.

证法二：因为EB⊥平面ABD，AB⊥BD，

故以B为原点，建立如图所示的空间直角坐标系B-xyz.

由已知可得＝，＝(3，－2,0)，＝(0，－1，)，

设平面ADF的法向量是n＝(x，y，z)．

由得

令y＝3，则n＝(2,3，)．

又因为·n＝0，所以⊥n，

又EM⊄平面ADF，故EM∥平面ADF.

(2)由(1)中证法二可知平面ADF的一个法向量是n＝(2,3，)．

易得平面BFD的一个法向量是m＝(0，－，1)．

所以cos〈m，n〉＝＝－，

又二面角A-FD-B为锐角，

故二面角A-FD-B的余弦值大小为.

9．(2019·河南郑州一模)如图所示，在四棱锥P-ABCD中，PA⊥平面ABCD，△DAB≌△DCB，E为线段BD上的一点，且EB＝ED＝EC＝BC，连接CE并延长交AD于F.

(1)若G为PD的中点，求证：平面PAD⊥平面CGF；

(2)若BC＝2，PA＝3，求平面BCP与平面DCP所成锐二面角的余弦值．

解：(1)证明：在△BCD中，EB＝ED＝EC＝BC，

故∠BCD＝，∠CBE＝∠CEB＝，

连接AE，

∵△DAB≌△DCB，∴△EAB≌△ECB，

从而有∠FED＝∠BEC＝∠AEB＝，AE＝CE＝DE.

∴∠AEF＝∠FED＝.

故EF⊥AD，AF＝FD.

又PG＝GD，∴FG∥PA.

又PA⊥平面ABCD，故GF⊥平面ABCD，

∴GF⊥AD，

又GF∩EF＝F，故AD⊥平面CFG.

又AD⊂平面PAD，

∴平面PAD⊥平面CGF.

(2)以点A为坐标原点建立如图所示的空间直角坐标系，

则A(0,0,0)，B(2,0,0)，C(3，，0)，D(0，2，0)，P(0,0,3)．

故＝(1，，0)，＝(－3，－，3)，＝(－3，，0)．

设平面BCP的一个法向量为n1＝(1，y1，z1)，

则解得

即n1＝.

设平面DCP的一个法向量为n2＝(1，y2，z2)，

则解得

即n2＝(1，，2)．

从而平面BCP与平面DCP所成锐二面角的余弦值为＝＝.

10．(2017·全国卷Ⅱ)如图，四棱锥P-ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB＝BC＝AD，∠BAD＝∠ABC＝90°，E是PD的中点．

(1)证明：直线CE∥平面PAB；

(2)点M在棱PC上，且直线BM与底面ABCD所成角为45°，求二面角M-AB-D的余弦值．

解：(1)取PA的中点F，连接EF，BF.

因为E是PD的中点，

所以EF∥AD，EF＝AD.

由∠BAD＝∠ABC＝90°得BC∥AD，

又BC＝AD，所以EF綊BC，

四边形BCEF是平行四边形，CE∥BF，

又BF⊂平面PAB，CE⊄平面PAB，故CE∥平面PAB.

(2)由已知得BA⊥AD，以A为坐标原点，的方向为x轴正方向，||为单位长，建立如图所示的空间直角坐标系A-xyz，则A(0,0,0)，B(1,0,0)，C(1,1,0)，P(0,1，)，＝(1,0，－)，＝(1,0,0)．设M(x，y，z)(0＜x＜1)，则＝(x－1，y，z)，＝(x，y－1，z－)．

因为BM与底面ABCD所成的角为45°，

而n＝(0,0,1)是底面ABCD的法向量，

所以|cos〈，n〉|＝sin 45°，

＝，

即(x－1)2＋y2－z2＝0.①

又M在棱PC上，设＝λ，

则x＝λ，y＝1，z＝－λ.②

由①②解得(舍去)，或

所以M，从而＝.

设m＝(x0，y0，z0)是平面ABM的法向量，

则

即

所以可取m＝(0，－，2)．

于是cos〈m，n〉＝＝.

易知所求二面角为锐角．

因此二面角M-AB-D的余弦值为.

11．如图，在四棱锥P-ABCD中，AD∥BC，∠ADC＝∠PAB＝90°，BC＝CD＝AD，E为棱AD的中点，异面直线PA与CD所成的角为90°.

(1)在平面PAB内找一点M，使得直线CM∥平面PBE，并说明理由；

(2)若二面角P-CD-A的大小为45°，求直线PA与平面PCE所成角的正弦值．

解：(1)在梯形ABCD中，AB与CD不平行．

如图，延长AB，DC，相交于点M(M∈平面PAB)，点M即为所求的一个点．

理由如下：

由已知，BC∥ED，且BC＝ED.

所以四边形BCDE是平行四边形，从而CM∥EB.

又EB⊂平面PBE，CM⊄平面PBE，

所以CM∥平面PBE.

(说明：延长AP至点N，使得AP＝PN，则所找的点可以是直线MN上任意一点)

(2)解法一：由已知，CD⊥PA，CD⊥AD，PA∩AD＝A，

所以CD⊥平面PAD.

从而CD⊥PD.

所以∠PDA是二面角P-CD-A的平面角．所以∠PDA＝45°.

设BC＝1，则在Rt△PAD中，PA＝AD＝2.

过点A作AH⊥CE，交CE的延长线于点H，连接PH.

易知PA⊥平面ABCD，

又CE⊂平面ABCD，从而PA⊥CE.

于是CE⊥平面PAH.

所以平面PCE⊥平面PAH.

过A作AQ⊥PH于Q，则AQ⊥平面PCE.

所以∠APH是PA与平面PCE所成的角．

在Rt△AEH中，∠AEH＝45°，AE＝1，

所以AH＝.

在Rt△PAH中，PH＝＝，

所以sin∠APH＝＝.

解法二：由已知，CD⊥PA，CD⊥AD，PA∩AD＝A，

所以CD⊥平面PAD.

于是CD⊥PD.

从而∠PDA是二面角P-CD-A的平面角．

所以∠PDA＝45°.

由PA⊥AB，可得PA⊥平面ABCD.

设BC＝1，则在Rt△PAD中，PA＝AD＝2.

作Ay⊥AD，以A为原点，以，的方向分别为x轴、z轴的正方向，建立如图所示的空间直角坐标系A-xyz，

则A(0,0,0)，P(0,0,2)，C(2,1,0)，E(1,0,0)，

所以＝(1,0，－2)，＝(1,1,0)，＝(0,0,2)．

设平面PCE的法向量n＝(x，y，z)，

由得

设x＝2，解得n＝(2，－2,1)．

设直线PA与平面PCE所成角为α，

则sinα＝＝＝.

所以直线PA与平面PCE所成角的正弦值为.

12．(2019·江西南昌二中月考)如图，在等腰梯形ABCD中，∠ABC＝60°，CD＝2，AB＝4，点E为AB的中点，现将该梯形中的三角形EBC沿线段EC折起，形成四棱锥B-AECD.

(1)在四棱锥B-AECD中，求证：AD⊥BD；

(2)若平面BEC与平面AECD所成二面角的平面角为120°，求直线AE与平面ABD所成角的正弦值．

解：(1)证明：由三角形BEC沿线段EC折起前，∠ABC＝60°，CD＝2，AB＝4，点E为AB的中点，得三角形BEC沿线段EC折起后，四边形AECD为菱形，边长为2，∠DAE＝60°，如图，取EC的中点F，连接DF，BF，DE，

∵△BEC和△DEC均为正三角形，

∴EC⊥BF，EC⊥DF, 又BF∩DF＝F，

∴EC⊥平面BFD，∵AD∥EC，∴AD⊥平面BFD，

∵BD⊂平面BFD，∴AD⊥BD.

(2)以F为坐标原点，建立如图的空间直角坐标系，

由EC⊥平面BFD，知z轴在平面BFD内，

∵BF⊥EC，DF⊥EC，

∴∠BFD为平面BEC与平面AECD所成二面角的平面角，

∴∠BFD＝120°，∴∠BFz＝30°，

又∵BF＝，∴点B的横坐标为－，点B的竖坐标为.

因D(，0,0)，E(0,1,0)，A(，2,0)，

B，

故＝(－，－1,0)，＝，＝(0，－2，0)．

设平面ABD的法向量为n＝(x，y，z)，

∴

得

令x＝1，得y＝0，z＝，∴平面ABD的一个法向量为n＝(1,0，)，

∴cos〈，n〉＝＝

＝－，

∵直线AE与平面ABD所成角为锐角，

∴直线AE与平面ABD所成角的正弦值为.