2020版新一线高考文科数学（北师大版）一轮复习教学案：第7章第2节　空间图形的基本关系与公理

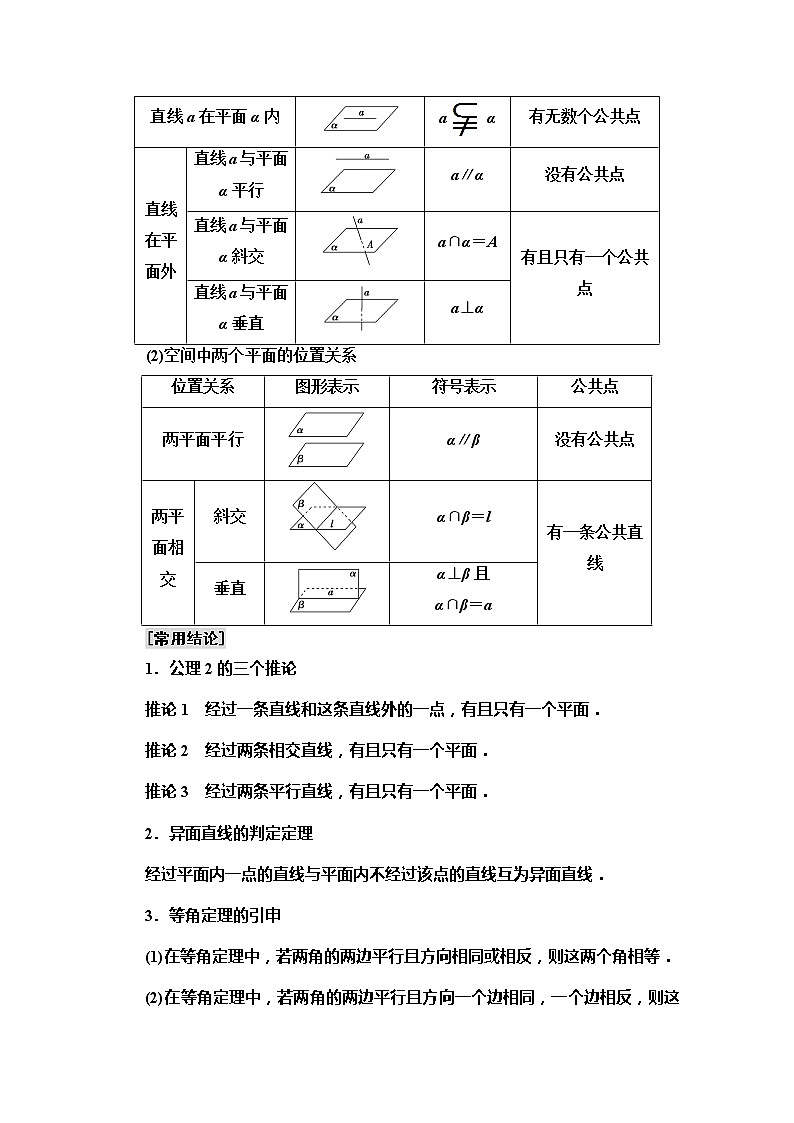
第二节　空间图形的基本关系与公理[考纲传真]　1.理解空间直线、平面位置关系的定义.2.了解可以作为推理依据的公理和定理.3.能运用公理、定理和已获得的结论证明一些空间位置关系的简单命题．1．空间图形的公理(1)公理1：过不在一条直线上的三点，有且只有一个平面(即可以确定一个平面)．(2)公理2：如果一条直线上的两点在一个平面内，那么这条直线在此平面内(即直线在平面内)．(3)公理3：如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线．(4)公理4：平行于同一条直线的两条直线平行．2．空间中两直线的位置关系(1)空间中两直线的位置关系(2)异面直线所成的角①定义：过空间任意一点P分别引两条异面直线a，b的平行线l1，l2(a∥l1，b∥l2)，这两条相交直线所成的锐角(或直角)就是异面直线a，b所成的角．②范围：.(3)定理(等角定理)空间中，如果两个角的两条边分别对应平行，那么这两个角相等或互补．3．空间中直线与平面、平面与平面的位置关系(1)空间中直线与平面的位置关系位置关系图形表示符号表示公共点直线a在平面α内aα有无数个公共点直线在平面外直线a与平面α平行a∥α没有公共点直线a与平面α斜交a∩α＝A有且只有一个公共点直线a与平面α垂直a⊥α(2)空间中两个平面的位置关系位置关系图形表示符号表示公共点两平面平行α∥β没有公共点两平面相交斜交α∩β＝l有一条公共直线垂直α⊥β且α∩β＝a1．公理2的三个推论推论1　经过一条直线和这条直线外的一点，有且只有一个平面．推论2　经过两条相交直线，有且只有一个平面．推论3　经过两条平行直线，有且只有一个平面．2．异面直线的判定定理经过平面内一点的直线与平面内不经过该点的直线互为异面直线．3．等角定理的引申(1)在等角定理中，若两角的两边平行且方向相同或相反，则这两个角相等．(2)在等角定理中，若两角的两边平行且方向一个边相同，一个边相反，则这两个角互补．[基础自测]1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”)(1)两个平面α，β有一个公共点A，就说α，β相交于过A点的任意一条直线． (　　)(2)两两相交的三条直线最多可以确定三个平面． (　　)(3)如果两个平面有三个公共点，则这两个平面重合． (　　)(4)若直线a不平行于平面α，且a⃘α，则α内的所有直线与a异面． (　　)[答案]　(1)×　(2)√　(3)×　(4)×2．(教材改编)如图所示，在正方体ABCD­A1B1C1D1中，E，F分别是AB，AD的中点，则异面直线B1C与EF所成的角的大小为(　　)A．30°　　　　 B．45°C．60° D．90°C　[连接B1D1，D1C(图略)，则B1D1∥EF，故∠D1B1C为所求的角，又B1D1＝B1C＝D1C，∴∠D1B1C＝60°.]3．(教材改编)下列命题正确的是(　　)A．经过三点确定一个平面B．经过一条直线和一个点确定一个平面C．四边形确定一个平面D．两两相交且不共点的三条直线确定一个平面D　[根据确定平面的公理和推论知选项D正确．]4．已知空间四边形的两条对角线相互垂直，顺次连接四边中点的四边形 一定是(　　)A．空间四边形 B．矩形C．菱形 D．正方形B　[四边形的相邻两边分别平行于空间四边形的两角对角线，故选B．]5．已知直线a，b分别在两个不同的平面α，β内，则“直线a和直线b相交”是“平面α和平面β相交”的(　　)A．充分不必要条件 B．必要不充分条件C．充要条件 D．既不充分也不必要条件A　[由题意知aα，bβ，若a，b相交，则a，b有公共点，从而α，β有公共点，可得出α，β相交；反之，若α，β相交，则a，b的位置关系可能为平行、相交或异面．因此“直线a和直线b相交”是“平面α和平面β相交”的充分不必要条件．故选A．]空间图形的公理及其应用 【例1】　(1)以下命题中，正确命题的个数是(　　)①不共面的四点中，其中任意三点不共线；②若点A，B，C，D共面，点A，B，C，E共面，则A，B，C，D，E共面；③若直线a，b共面，直线a，c共面，则直线b，c共面；④依次首尾相接的四条线段必共面．A．0　　   B．1　　　　C．2　　　　D．3B　[①正确，可以用反证法证明，假设任意三点共线，则四个点必共面，与不共面的四点矛盾；②中若点A，B，C在同一条直线上，则A，B，C，D，E不一定共面，故②错误；③中，直线b，c可能是异面直线，故③错误；④中，当四条线段构成空间四边形时，四条线段不共面，故④错误．](2)如图，正方体ABCD­A1B1C1D1中，E，F分别是AB和AA1的中点．求证：①E，C，D1，F四点共面；②CE，D1F，DA三线共点．[解]　①如图，连接EF，CD1，A1B．∵E，F分别是AB，AA1的中点，∴EF∥BA1.又∵A1B∥D1C，∴EF∥CD1，∴E，C，D1，F四点共面．②∵EF∥CD1，EF<CD1，∴CE与D1F必相交，设交点为P，则由P∈直线CE，CE平面ABCD，得P∈平面ABCD．同理P∈平面ADD1A1.又平面ABCD∩平面ADD1A1＝DA，∴P∈直线DA，∴CE，D1F，DA三线共点．[规律方法]　共点、共线、共面问题的证明方法(1)证明点共线问题：①公理法：先找出两个平面，然后证明这些点都是这两个平面的公共点，再根据基本公理3证明这些点都在交线上；②同一法：选择其中两点确定一条直线，然后证明其余点也在该直线上．(2)证明线共点问题：先证两条直线交于一点，再证明第三条直线经过该点．(3)证明点、直线共面问题：①纳入平面法：先确定一个平面，再证明有关点、线在此平面内；②辅助平面法：先证明有关的点、线确定平面α，再证明其余元素确定平面β，最后证明平面α，β重合． (1)如图是正方体或四面体，P，Q，R，S分别是所在棱的中点，则这四个点不共面的一个图是   (　　)A　　　　　B　　　　C　　　　DD　[根据异面直线的判定定理，选项D中PS与QR是异面直线，则四点P，Q，R，S不共面．故选D．](2)如图，在正方体ABCD­A1B1C1D1中，O为正方形ABCD的中心，H为直线B1D与平面ACD1的交点．求证：D1，H，O三点共线．[证明]　如图，连接BD，B1D1，则BD∩AC＝O，因为BB1DD1，所以四边形BB1D1D为平行四边形，又H∈B1D，B1D平面BB1D1D，则H∈平面BB1D1D，因为平面ACD1∩平面BB1D1D＝OD1，所以H∈OD1.即D1，H，O三点共线． 空间两条直线的位置关系 【例2】　(1)已知a，b，c为三条不同的直线，且a平面α，b平面β，α∩β＝c，给出下列命题：①若a与b是异面直线，则c至少与a，b中的一条相交；②若a不垂直于c，则a与b一定不垂直；③若a∥b，则必有a∥c.其中真命题有________．(填序号)(2)在图中，G，H，M，N分别是正三棱柱的顶点或所在棱的中点，则表示直线GH，MN是异面直线的图形有________(填上所有正确答案的序号)．①　　　②　　　③　　　　④(1)①③　(2)②④　[(1)对于①，若c与a，b都不相交，则c∥a，c∥b，从而a∥b，这与a与b是异面直线矛盾，故①正确．对于②，a与b可能异面垂直，故②错误．对于③，由a∥b可知a∥β，又α∩β＝c，从而a∥c，故③正确．(2)图①中，直线GH∥MN；图②中，G，H，N三点共面，但M∉平面GHN，因此直线GH与MN异面；图③中，连接MG(图略)，GM∥HN，因此GH与MN共面；图④中，G，M，N共面，但H∉平面GMN，因此GH与MN异面，所以在图②④中，GH与MN异面．][规律方法]　异面直线的判定方法 (1)已知a，b是异面直线，直线c平行于直线a，那么c与b(　　)A．一定是异面直线　　 B．一定是相交直线C．不可能是平行直线 D．不可能是相交直线(2)如图所示，正方体ABCD­A1B1C1D1中，M，N分别为棱C1D1，C1C的中点，有以下四个结论：①直线AM与CC1是相交直线；②直线AM与BN是平行直线；③直线BN与MB1是异面直线；④直线AM与DD1是异面直线．其中正确的结论为________．(把你认为正确的结论的序号都填上)(1)C　(2)③④　[(1)c与b可能相交，也可能异面，但可不能平行，故选C．(2)根据两条异面直线的判定定理知，③④正确．] 异面直线所成的角 【例3】　(1)(2018·全国卷Ⅱ)在正方体ABCD－A1B1C1D1中，E为棱CC1的中点，则异面直线AE与CD所成角的正切值为(　　)A．　　　　B．　　　　C．　　　　D．(2)如图，在长方体ABCD­A1B1C1D1中，AB＝2，BC＝1，BB1＝1，P是AB的中点，则异面直线BC1与PD所成的角等于(　　)A．30°   B．45°  C．60°   D．90°(1)C　(2)C　[(1)如图，连接BE，因为AB∥CD，所以异面直线AE与CD所成的角等于相交直线AE与AB所成的角，即∠EAB．不妨设正方体的棱长为2，则CE＝1，BC＝2，由勾股定理得BE＝.又由AB⊥平面BCC1B1可得AB⊥BE，所以tan∠EAB＝＝.故选C．(2)取CD的中点Q，连接BQ，C1Q∵P是AB的中点，∴BQ∥PD∴∠C1BQ是异面直线BC1与PD所成的角．在△C1BQ中，C1B＝BQ＝C1Q＝，∴∠C1BQ＝60°，即异面直线BC1与PD所成的角等于60°，故选C．][规律方法]　用平移法求异面直线所成的角的步骤(1)一作：根据定义作平行线，作出异面直线所成的角；(2)二证：证明作出的角是异面直线所成的角；(3)三求：解三角形，求出作出的角．如果求出的角是锐角或直角，则它就是要求的角；如果求出的角是钝角，则它的补角才是要求的角． (1)已知P是△ABC所在平面外的一点，M，N分别是AB、PC的中点，若MN＝BC＝4，PA＝4，则异面直线PA与MN所成角的大小是(　　)A．30° B．45°C．60° D．90°(2)如图，已知圆柱的轴截面ABB1A1是正方形，C是圆柱下底面弧AB的中点，C1是圆柱上底面弧A1B1的中点，那么异面直线AC1与BC所成角的正切值为________．(1)A　(2)　[(1)取AC的中点O，连接OM，ON，则OMBC，ONPA．∴∠ONM就是异面直线PA与MN所成的角．在△OMN中，MN＝4，OM＝2，ON＝2，∴cos∠ONM＝＝＝，∴∠ONM＝30°即异面直线PA与MN所成角的大小为30°，故选A．(2)取圆柱下底面弧AB的另一中点D，连接C1D，AD，因为C是圆柱下底面弧AB的中点，所以AD∥BC，所以直线AC1与AD所成角等于异面直线AC1与BC所成角，因为C1是圆柱上底面弧A1B1的中点，所以C1D⊥圆柱下底面，所以C1D⊥AD．因为圆柱的轴截面ABB1A1是正方形，所以C1D＝AD，所以直线AC1与AD所成角的正切值为，所以异面直线AC1与BC所成角的正切值为.] 1．(2017·全国卷Ⅱ)已知直三棱柱ABC­A1B1C1中，∠ABC＝120°，AB＝2，BC＝CC1＝1，则异面直线AB1与BC1所成角的余弦值为(　　)A．　　　B．　　　C．　　　D．C　[将直三棱柱ABC­A1B1C1补形为直四棱柱ABCD­A1B1C1D1，如图所示，连接AD1，B1D1，BD．由题意知∠ABC＝120°，AB＝2，BC＝CC1＝1，所以AD1＝BC1＝，AB1＝，∠DAB＝60°.在△ABD中，由余弦定理知BD2＝22＋12－2×2×1×cos 60°＝3，所以BD＝，所以B1D1＝.又AB1与AD1所成的角即为AB1与BC1所成的角θ，所以cos θ＝＝＝.故选C．]2．(2016·全国卷Ⅰ)平面α过正方体ABCD­A1B1C1D1的顶点A，α∥平面CB1D1，α∩平面ABCD＝m，α∩平面ABB1A1＝n，则m，n所成角的正弦值为(　　)A．　　　　B．　　　　C．　　　　D．A　[根据平面与平面平行的性质，将m，n所成的角转化为平面CB1D1与平面ABCD的交线及平面CB1D1与平面ABB1A1的交线所成的角．设平面CB1D1∩平面ABCD＝m1.∵平面α∥平面CB1D1，∴m1∥m.又平面ABCD∥平面A1B1C1D1，且平面CB1D1∩平面A1B1C1D1＝B1D1，∴B1D1∥m1.∴B1D1∥m.∵平面ABB1A1∥平面DCC1D1，且平面CB1D1∩平面DCC1D1＝CD1，同理可证CD1∥n.因此直线m与n所成的角即直线B1D1与CD1所成的角．在正方体ABCD­A1B1C1D1中，△CB1D1是正三角形，故直线B1D1与CD1所成角为60°，其正弦值为.]