

还剩12页未读,
继续阅读
2020版高考数学新设计一轮复习浙江专版讲义:第七章第二节空间几何体的表面积与体积
展开
第二节空间几何体的表面积与体积
1.圆柱、圆锥、圆台的侧面展开图及侧面积公式
圆柱
圆锥
圆台
侧面展开图
侧面积公式
S圆柱侧=2πrl
S圆锥侧=πrl
S圆台侧=π(r+r′)l
2.空间几何体的表面积与体积公式
名称
几何体
表面积
体积
柱体(棱柱和圆柱)
S表面积=S侧+2S底
V=Sh
锥体(棱锥和圆锥)
S表面积=S侧+S底
V=Sh
台体(棱台和圆台)
S表面积=S侧+S上+S下
V=(S上+S下+)h
球
S=4πR2
V=πR3
[小题体验]
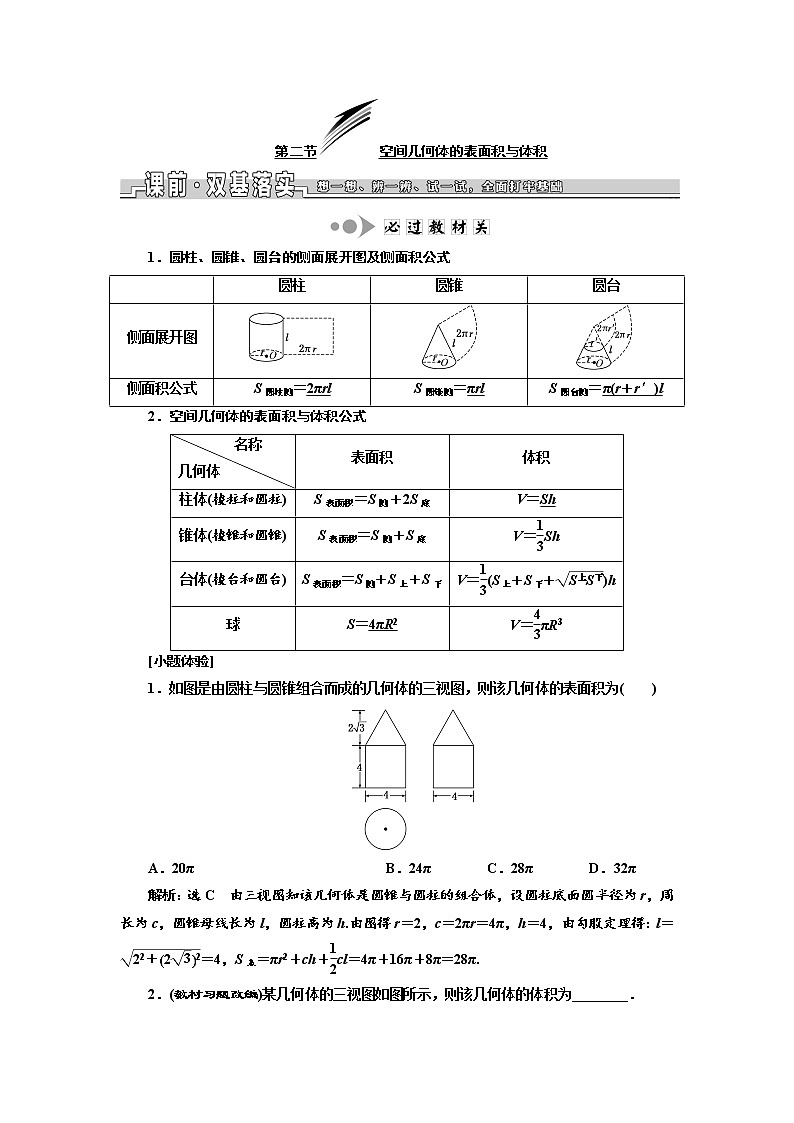
1.如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )
A.20π B.24π C.28π D.32π
解析:选C 由三视图知该几何体是圆锥与圆柱的组合体,设圆柱底面圆半径为r,周长为c,圆锥母线长为l,圆柱高为h.由图得r=2,c=2πr=4π,h=4,由勾股定理得:l==4,S表=πr2+ch+cl=4π+16π+8π=28π.
2.(教材习题改编)某几何体的三视图如图所示,则该几何体的体积为________.
解析:由三视图可知,该几何体是一个直三棱柱,其底面为侧视图,该侧视图是底边为2,高为的三角形,正视图的长为三棱柱的高,故h=3,所以该几何体的体积V=S·h=×3=3.
答案:3
3.若球O的表面积为4π,则该球的体积为________.
解析:由题可得,设该球的半径为r,则其表面积为S=4πr2=4π,解得r=1.所以其体积为V=πr3=π.
答案:π
1.求组合体的表面积时,组合体的衔接部分的面积问题易出错.
2.由三视图计算几何体的表面积与体积时,由于几何体的还原不准确及几何体的结构特征认识不准易导致失误.
3.易混侧面积与表面积的概念.
[小题纠偏]
1.(教材习题改编)圆柱的底面直径与高都等于球的直径,则球的体积与圆柱体积之比为________,球的表面积与圆柱的侧面积之比为________.
答案:2∶3 1∶1
2.若某几何体的三视图如图所示,则此几何体的表面积是________.
解析:由三视图可知,该几何体由一个正四棱柱和一个棱台组成,其表面积S=3×4×2+2×2×2+4×2×2+4×6+×(2+6)×2×2=72+16.
答案:72+16
[题组练透]
1.某几何体的三视图如图所示,则该几何体的表面积等于( )
A.8+2
B.11+2
C.14+2
D.15
解析:选B 由三视图知,该几何体是一个直四棱柱,上、下底面为直角梯形,如图所示.直角梯形斜腰长为=,所以底面周长为4+,侧面积为2×(4+)=8+2,两底面的面积和为2××1×(1+2)=3,所以该几何体的表面积为8+2+3=11+2.
2.(2018·浙江新高考联盟高三期初联考)如图是某四棱锥的三视图,则该几何体的表面积等于( )
A.34+6 B.44+12
C.34+6 D.32+6
解析:选A 由三视图知几何体底面是一个长为6,宽为2的矩形,高为4的四棱锥,所以该几何体的表面积为×6×2+×6×4+2××2×5+6×2=34+6,故选A.
3.如图,网格纸上小正方形的边长为1,粗线是一个棱锥的三视图,则该棱锥的表面积为( )
A.6+4+2
B.8+4
C.6+6
D.6+2+4
解析:选A 由三视图可知该棱锥为如图所示的四棱锥PABCD,S△PAB=S△PAD=S△PDC=×2×2=2,S△PBC=×2×2×sin 60°=2,S四边形ABCD=2×2=4,故该棱锥的表面积为6+4+2.
[谨记通法]
几何体的表面积的求法
(1)求表面积问题的思路是将立体几何问题转化为平面问题,即空间图形平面化,这是解决立体几何的主要出发点.
(2)求不规则几何体的表面积时,通常将所给几何体分割成基本的柱、锥、台体,先求这些柱、锥、台体的表面积,再通过求和或作差求得几何体的表面积.注意衔接部分的处理.
[典例引领]
1.(2018·金华高三期末考试)某几何体的三视图如图所示,则该几何体的体积为( )
A. B.
C. D.
解析:选D 由三视图可知该几何体是一个以俯视图为底面的四棱锥,其直观图如图所示.底面ABCD的面积为2×2=4,高PO=,故该几何体的体积V=×4×=.
2.(2018·宁波十校联考)某几何体的三视图如图所示,则该几何体的体积等于________,表面积等于________.
解析:如图,由三视图可知该几何体是底面半径为2,高为3的圆柱的一半,故该几何体的体积为×π×22×3=6π,
表面积为2××π×22+4×3+π×2×3=10π+12.
答案:6π 12+10π
[由题悟法]
有关几何体体积的类型及解题策略
常见类型
解题策略
球的体积问题
直接利用球的体积公式求解,在实际问题中要根据题意作出图形,构造直角三角形确定球的半径
锥体、柱体的体积问题
根据题设条件求出所给几何体的底面积和高,直接套用公式求解
以三视图为载体的几何体体积问题
将三视图还原为几何体,利用空间几何体的体积公式求解
不规则几何体的体积问题
常用分割或补形的思想,若几何体的底不规则,也需采用同样的方法,将不规则的几何体或平面图形转化为规则的几何体或平面图形,易于求解
[即时应用]
1.(2018·杭州高级中学模拟)一个几何体的三视图如图所示,则该几何体的体积为( )
A.1 B.
C. D.
解析:选C 由题可得,该几何体是一个四棱锥,底面是上下底边分别为1和2,高为1的直角梯形,又四棱锥的高为1.所以该几何体的体积为V=××(1+2)×1×1=.
2.(2019·台州高三适考)如图是一个几何体的三视图,则该几何体的体积为________,几何体中最长棱的长是________.
解析:由三视图可知,该几何体是棱长为2的正方体ABCDA1B1C1D1中的三棱锥MA1B1N,如图所示,M是棱AB上靠近点A的一个三等分点,N是棱C1D1的中点,所以VMA1B1N=××2×2×2=.又A1B1=2,A1N=B1N==,A1M==,B1M==,MN==
,所以该几何体中最长棱的长是.
答案:
3.(2018·温州高三一模)如图,一个简单几何体的三视图的正视图与侧视图都是边长为1的正三角形,其俯视图的轮廓为正方形,则该几何体的体积为________,表面积为________.
解析:如图,还原三视图为正四棱锥,易得正四棱锥的高为,底面积为1,体积V=×1×=;易得正四棱锥侧面的高为=1,所以表面积S=4××1×1+1=3.
答案: 3
[锁定考向]
与球相关的切、接问题是高考命题的热点,也是考生的难点、易失分点,命题角度多变.
常见的命题角度有:
(1)球与柱体的切、接问题;
(2)球与锥体的切、接问题.
[题点全练]
角度一:球与柱体的切、接问题
1.如图,已知球O是棱长为1的正方体ABCDA1B1C1D1的内切球,则平面ACD1截球O的截面面积为( )
A.π B.
C. D.π
解析:选C 平面ACD1截球O的截面为△ACD1的内切圆.因为正方体的棱长为1,所以AC=CD1=AD1=,所以内切圆的半径r=×tan 30°=,
所以S=πr2=π×=π.
2.(2018·金华一模)一个圆柱的轴截面是正方形,在圆柱内有一个球O,该球与圆柱的上、下底面及母线均相切.记球O的体积为V1,圆柱内除了球之外的几何体体积为V2,则的值为________.
解析:如图,设圆柱的底面半径为r,则圆柱的高为2r,球O的半径为r,∴球O的体积V1=πr3,圆柱内除了球之外的几何体体积 V2=πr2×2r-πr3=πr3,
∴==2.
答案:2
角度二:球与锥体的切、接问题
3.(2018·绍兴质检)四棱锥PABCD的底面ABCD是边长为6的正方形,且PA=PB=PC=PD,若一个半径为1的球与此四棱锥所有面都相切,则该四棱锥的高是( )
A.6 B.5
C. D.
解析:选D 过点P作PH⊥平面ABCD于点H.由题知,四棱锥PABCD是正四棱锥,内切球的球心O应在四棱锥的高PH上.过正四棱锥的高作组合体的轴截面如图,其中PE,PF是斜高,M为球面与侧面的一个切点.设PH=h,易知Rt△PMO∽Rt△PHF,所以=,即=,解得h=.
4.(2018·嘉兴一模)如图是某几何体的三视图,正视图是等边三角形,侧视图和俯视图为直角三角形,则该几何体外接球的表面积为( )
A. B.8π
C.9π D.
解析:选D 如图,该几何体为三棱锥ABCD,设三棱锥外接球的球心为O,O1,O2分别为△BCD,△ABD的外心,依题意得,OO1=AB=,O1D=CD=,∴球的半径R== ,∴该几何体外接球的表面积S=4πR2=.
[通法在握]
解决与球有关的切、接问题,其通法是作截面,将空间几何问题转化为平面几何问题求解,其解题的思维流程是:
[演练冲关]
1.一个六棱柱的底面是正六边形,侧棱垂直于底面,所有棱的长都为1,顶点都在同一个球面上,则该球的体积为( )
A.20π B.
C.5π D.
解析:选D 由题意知六棱柱的底面正六边形的外接圆半径r=1,其高h=1,∴球半径为R===,∴该球的体积V=πR3=×3π=.
2.(2018·镇海期中)一个棱长为6的正四面体纸盒内放一个正方体,若正方体可以在纸盒内任意转动,则正方体体积的最大值为________.
解析:由题可得,要使正方体可以在纸盒内任意转动,则只需该正方体在正四面体的内接球内即可.因为正四面体的棱长为6,所以其底面正三角形的高为3,正四面体的高为2,则该正四面体的内球的半径为,设该正方体的边长为a,要满足条件,则a≤,即a≤.所以正方体的最大体积为V=a3≤2.
答案:2
一抓基础,多练小题做到眼疾手快
1.(2018·浙江名校联考)“某几何体的三视图完全相同”是“该几何体为球”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解析:选B 由题可得,球的三个视图都是圆,所以三视图完全相同;三视图完全相同的几何体除了球,还有正方体,所以是必要不充分条件.
2.(2018·长兴中学适应性测试)一个几何体的三视图如图所示,则该几何体的体积为( )
A.64 B.72
C.80 D.112
解析:选C 由题可得,该几何体是一个棱长为4的正方体与一个底面是边长为4的正方形,高为3的四棱锥的组合体,所以其体积为V=43+×42×3=80.
3.(2019·杭二月考)一个几何体的三视图如图所示,则该几何体的体积为( )
A.π+ B.2π+
C.2π+ D.π+
解析:选A 由三视图知,该几何体的上半部分是一个三棱锥,下半部分是一个圆柱.由题图中的数据知V圆柱=π×12×1=π,三棱锥垂直于底面的侧面是边长为2的等边三角形,故其高即为三棱锥的高,故三棱锥的高为,由于三棱锥底面为一等腰直角三角形,且斜边长为2,因此两直角边长都是,则底面三角形的面积是××=1,故V三棱锥=×1×=,故该几何体的体积为π+.
4.(2018·嘉兴模拟)如图是一个几何体的三视图,若它的体积是3,则a=________,该几何体的表面积为________.
解析:由题可得,该几何体是一个水平放置的三棱柱,其底面是一个底边长为2、高为a的等腰三角形,高为3.因为其体积为3,所以V=×2a×3=3a=3,解得a=.所以该几何体的表面积为S=2××2×+2×3×3=2+18.
答案: 2+18
5.(2018·丽水模拟)若三棱锥PABC的最长的棱PA=2,且各面均为直角三角形,则此三棱锥的外接球的体积是________,表面积是________.
解析:如图,根据题意,可把该三棱锥补成长方体,则该三棱锥的外接球即该长方体的外接球,易得外接球的半径R=PA=1,所以该三棱锥的外接球的体积V=×π×13=π,表面积S=4πR2=4π.
答案:π 4π
二保高考,全练题型做到高考达标
1.圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面的半径为( )
A.7 B.6
C.5 D.3
解析:选A 设圆台较小底面半径为r,
则另一底面半径为3r.
由S=π(r+3r)·3=84π,解得r=7.
2.(2018·全国卷Ⅰ)已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( )
A.12π B.12π
C.8π D.10π
解析:选B 设圆柱的轴截面的边长为x,
则x2=8,得x=2,
∴S圆柱表=2S底+S侧=2×π×()2+2π××2
=12π.故选B.
3.(2018·温州十校联考)已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的体积是( )
A.4 B.
C.8 D.
解析:选B 由题可得,该几何体是一个底面为长方形的四棱锥,所以其体积为V=×4×2×2=.
4.(2018·兰州实战考试)一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个等腰直角三角形,则该几何体外接球的体积为( )
A.π B.
C.3π D.3
解析:选A 由题意得,该几何体为四棱锥,且该四棱锥的外接球即为棱长为1的正方体的外接球,其半径为,故体积为π3=π,故选A.
5.(2018·宁波十校联考)如图,某多面体的三视图中正视图、侧视图和俯视图的外轮廓分别为直角三角形、直角梯形和直角三角形,则该多面体的各条棱中,最长的棱的长度为( )
A.2 B.
C.2 D.
解析:选C 由题可得,该几何体是水平放置的四棱锥,其底面是一个直角梯形.所以其最长的棱的长度为=2.
6.(2018·宁波一模)某空间几何体的三视图如图所示,则该几何体的体积为( )
A.
B.
C.
D.
解析:选B 由三视图得,该几何体是从四棱锥PABCD中挖去半个圆锥后剩余的部分,四棱锥的底面是以2为边长的正方形、高是2,圆锥的底面半径是1、高是2,则所求的体积V=×2×2×2-×π×12×2=.
7.(2018·衢州调研)已知某几何体的三视图如图所示,则此几何体的体积是________;表面积是________.
解析:该几何体是一个三棱锥,其高为2,其底面是一个等腰直角三角形,腰长为,所以其体积为V=××()2×2=,表面积为S=×2×+×()2+×2×2+××=3++.
答案: 3++
8.(2018·杭州模拟)已知矩形ABCD的顶点都在半径为4的球O的球面上,且AB=3,BC=2,则棱锥OABCD的体积为________.
解析:依题意得,球心O在底面ABCD上的射影是矩形ABCD的中心,因此棱锥OABCD的高等于=,
所以棱锥OABCD的体积等于×3×2×=.
答案:
9.(2019·舟山六校联考)某四面体的三视图如图所示,其中侧视图与俯视图都是腰长为2的等腰直角三角形,正视图是边长为2的正方形,则此四面体的体积为________.
解析:由三视图可知,该四面体是四面体ABCD,如图,其中,BE⊥底面ACD,AD=DC=BE=2,则该四面体的体积为××2×2×2=.
答案:
10.(2018·武汉调研)已知正四棱锥的顶点都在同一球面上,且该棱锥的高为4,底面边长为2,则该球的表面积为________.
解析:如图,正四棱锥PABCD的外接球的球心O在它的高PO1上,设球的半径为R,为底面边长为2,所以AC=4.在Rt△AOO1中,R2=(4-R)2+22,所以R=,所以球的表面积S=4πR2=25π.
答案:25π
三上台阶,自主选做志在冲刺名校
1.(2018·广西质检)高为4的直三棱柱被削去一部分后得到一个几何体,它的直观图和三视图中的侧视图、俯视图如图所示,则该几何体的体积与原直三棱柱的体积的比值为( )
A. B.
C. D.
解析:选C 由侧视图、俯视图知该几何体是高为2、底面积为×2×(2+4)=6的四棱锥,其体积为4.易知直三棱柱的体积为8,则该几何体的体积与原直三棱柱的体积的比值为,故选C.
2.(2018·温州一模)三棱锥的三视图如图所示,则该三棱锥外接球的体积为( )
A.4π B.2π
C.4π D.2π
解析:选A 三棱锥的直观图如图,设H为三棱锥PABC外接球的球心,O1为△PAC外接圆的圆心,O2为△ABC外接圆的圆心,取AC的中点O,连接PO,HO1,O2H,HB,结合三视图易知OO1=PO=,O2B=AB=×=.∵平面PAC⊥平面ABC,HO2⊥平面ABC,HO2⊄平面PAC,∴HO2∥平面PAC,∵PO⊥平面ABC,∴OO1∥HO2,连接OO2,易知OO2∥HO1,∴四边形HO1OO2为平行四边形,∴HO2=OO1=.在Rt△HO2B中,HB==,即三棱锥PABC外接球的半径为,故所求体积为×π×()3=4π.
3.已知A,B,C是球O的球面上三点,且AB=AC=3,BC=3,D为该球面上的动点,球心O到平面ABC的距离为球半径的一半,求三棱锥D ABC体积的最大值.
解:如图,在△ABC中,
∵AB=AC=3,BC=3,
∴由余弦定理可得
cos A==-,
∴sin A=.
设△ABC外接圆O′的半径为r,
则=2r,得r=3.
设球的半径为R,连接OO′,BO′,OB,则R2=2+32,解得R=2.
由图可知,当点D到平面ABC的距离为R时,三棱锥D ABC的体积最大,
∵S△ABC=×3×3×=,
∴三棱锥D ABC体积的最大值为××3=.
1.圆柱、圆锥、圆台的侧面展开图及侧面积公式
圆柱
圆锥
圆台
侧面展开图
侧面积公式
S圆柱侧=2πrl
S圆锥侧=πrl
S圆台侧=π(r+r′)l
2.空间几何体的表面积与体积公式
名称
几何体
表面积
体积
柱体(棱柱和圆柱)
S表面积=S侧+2S底
V=Sh
锥体(棱锥和圆锥)
S表面积=S侧+S底
V=Sh
台体(棱台和圆台)
S表面积=S侧+S上+S下
V=(S上+S下+)h
球
S=4πR2
V=πR3
[小题体验]
1.如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )
A.20π B.24π C.28π D.32π
解析:选C 由三视图知该几何体是圆锥与圆柱的组合体,设圆柱底面圆半径为r,周长为c,圆锥母线长为l,圆柱高为h.由图得r=2,c=2πr=4π,h=4,由勾股定理得:l==4,S表=πr2+ch+cl=4π+16π+8π=28π.
2.(教材习题改编)某几何体的三视图如图所示,则该几何体的体积为________.
解析:由三视图可知,该几何体是一个直三棱柱,其底面为侧视图,该侧视图是底边为2,高为的三角形,正视图的长为三棱柱的高,故h=3,所以该几何体的体积V=S·h=×3=3.
答案:3
3.若球O的表面积为4π,则该球的体积为________.
解析:由题可得,设该球的半径为r,则其表面积为S=4πr2=4π,解得r=1.所以其体积为V=πr3=π.
答案:π
1.求组合体的表面积时,组合体的衔接部分的面积问题易出错.
2.由三视图计算几何体的表面积与体积时,由于几何体的还原不准确及几何体的结构特征认识不准易导致失误.
3.易混侧面积与表面积的概念.
[小题纠偏]
1.(教材习题改编)圆柱的底面直径与高都等于球的直径,则球的体积与圆柱体积之比为________,球的表面积与圆柱的侧面积之比为________.
答案:2∶3 1∶1
2.若某几何体的三视图如图所示,则此几何体的表面积是________.
解析:由三视图可知,该几何体由一个正四棱柱和一个棱台组成,其表面积S=3×4×2+2×2×2+4×2×2+4×6+×(2+6)×2×2=72+16.
答案:72+16
[题组练透]
1.某几何体的三视图如图所示,则该几何体的表面积等于( )
A.8+2
B.11+2
C.14+2
D.15
解析:选B 由三视图知,该几何体是一个直四棱柱,上、下底面为直角梯形,如图所示.直角梯形斜腰长为=,所以底面周长为4+,侧面积为2×(4+)=8+2,两底面的面积和为2××1×(1+2)=3,所以该几何体的表面积为8+2+3=11+2.
2.(2018·浙江新高考联盟高三期初联考)如图是某四棱锥的三视图,则该几何体的表面积等于( )
A.34+6 B.44+12
C.34+6 D.32+6
解析:选A 由三视图知几何体底面是一个长为6,宽为2的矩形,高为4的四棱锥,所以该几何体的表面积为×6×2+×6×4+2××2×5+6×2=34+6,故选A.
3.如图,网格纸上小正方形的边长为1,粗线是一个棱锥的三视图,则该棱锥的表面积为( )
A.6+4+2
B.8+4
C.6+6
D.6+2+4
解析:选A 由三视图可知该棱锥为如图所示的四棱锥PABCD,S△PAB=S△PAD=S△PDC=×2×2=2,S△PBC=×2×2×sin 60°=2,S四边形ABCD=2×2=4,故该棱锥的表面积为6+4+2.
[谨记通法]
几何体的表面积的求法
(1)求表面积问题的思路是将立体几何问题转化为平面问题,即空间图形平面化,这是解决立体几何的主要出发点.
(2)求不规则几何体的表面积时,通常将所给几何体分割成基本的柱、锥、台体,先求这些柱、锥、台体的表面积,再通过求和或作差求得几何体的表面积.注意衔接部分的处理.
[典例引领]
1.(2018·金华高三期末考试)某几何体的三视图如图所示,则该几何体的体积为( )
A. B.
C. D.
解析:选D 由三视图可知该几何体是一个以俯视图为底面的四棱锥,其直观图如图所示.底面ABCD的面积为2×2=4,高PO=,故该几何体的体积V=×4×=.
2.(2018·宁波十校联考)某几何体的三视图如图所示,则该几何体的体积等于________,表面积等于________.
解析:如图,由三视图可知该几何体是底面半径为2,高为3的圆柱的一半,故该几何体的体积为×π×22×3=6π,
表面积为2××π×22+4×3+π×2×3=10π+12.
答案:6π 12+10π
[由题悟法]
有关几何体体积的类型及解题策略
常见类型
解题策略
球的体积问题
直接利用球的体积公式求解,在实际问题中要根据题意作出图形,构造直角三角形确定球的半径
锥体、柱体的体积问题
根据题设条件求出所给几何体的底面积和高,直接套用公式求解
以三视图为载体的几何体体积问题
将三视图还原为几何体,利用空间几何体的体积公式求解
不规则几何体的体积问题
常用分割或补形的思想,若几何体的底不规则,也需采用同样的方法,将不规则的几何体或平面图形转化为规则的几何体或平面图形,易于求解
[即时应用]
1.(2018·杭州高级中学模拟)一个几何体的三视图如图所示,则该几何体的体积为( )
A.1 B.
C. D.
解析:选C 由题可得,该几何体是一个四棱锥,底面是上下底边分别为1和2,高为1的直角梯形,又四棱锥的高为1.所以该几何体的体积为V=××(1+2)×1×1=.
2.(2019·台州高三适考)如图是一个几何体的三视图,则该几何体的体积为________,几何体中最长棱的长是________.
解析:由三视图可知,该几何体是棱长为2的正方体ABCDA1B1C1D1中的三棱锥MA1B1N,如图所示,M是棱AB上靠近点A的一个三等分点,N是棱C1D1的中点,所以VMA1B1N=××2×2×2=.又A1B1=2,A1N=B1N==,A1M==,B1M==,MN==
,所以该几何体中最长棱的长是.
答案:
3.(2018·温州高三一模)如图,一个简单几何体的三视图的正视图与侧视图都是边长为1的正三角形,其俯视图的轮廓为正方形,则该几何体的体积为________,表面积为________.
解析:如图,还原三视图为正四棱锥,易得正四棱锥的高为,底面积为1,体积V=×1×=;易得正四棱锥侧面的高为=1,所以表面积S=4××1×1+1=3.
答案: 3
[锁定考向]
与球相关的切、接问题是高考命题的热点,也是考生的难点、易失分点,命题角度多变.
常见的命题角度有:
(1)球与柱体的切、接问题;
(2)球与锥体的切、接问题.
[题点全练]
角度一:球与柱体的切、接问题
1.如图,已知球O是棱长为1的正方体ABCDA1B1C1D1的内切球,则平面ACD1截球O的截面面积为( )
A.π B.
C. D.π
解析:选C 平面ACD1截球O的截面为△ACD1的内切圆.因为正方体的棱长为1,所以AC=CD1=AD1=,所以内切圆的半径r=×tan 30°=,
所以S=πr2=π×=π.
2.(2018·金华一模)一个圆柱的轴截面是正方形,在圆柱内有一个球O,该球与圆柱的上、下底面及母线均相切.记球O的体积为V1,圆柱内除了球之外的几何体体积为V2,则的值为________.
解析:如图,设圆柱的底面半径为r,则圆柱的高为2r,球O的半径为r,∴球O的体积V1=πr3,圆柱内除了球之外的几何体体积 V2=πr2×2r-πr3=πr3,
∴==2.
答案:2
角度二:球与锥体的切、接问题
3.(2018·绍兴质检)四棱锥PABCD的底面ABCD是边长为6的正方形,且PA=PB=PC=PD,若一个半径为1的球与此四棱锥所有面都相切,则该四棱锥的高是( )
A.6 B.5
C. D.
解析:选D 过点P作PH⊥平面ABCD于点H.由题知,四棱锥PABCD是正四棱锥,内切球的球心O应在四棱锥的高PH上.过正四棱锥的高作组合体的轴截面如图,其中PE,PF是斜高,M为球面与侧面的一个切点.设PH=h,易知Rt△PMO∽Rt△PHF,所以=,即=,解得h=.
4.(2018·嘉兴一模)如图是某几何体的三视图,正视图是等边三角形,侧视图和俯视图为直角三角形,则该几何体外接球的表面积为( )
A. B.8π
C.9π D.
解析:选D 如图,该几何体为三棱锥ABCD,设三棱锥外接球的球心为O,O1,O2分别为△BCD,△ABD的外心,依题意得,OO1=AB=,O1D=CD=,∴球的半径R== ,∴该几何体外接球的表面积S=4πR2=.
[通法在握]
解决与球有关的切、接问题,其通法是作截面,将空间几何问题转化为平面几何问题求解,其解题的思维流程是:
[演练冲关]
1.一个六棱柱的底面是正六边形,侧棱垂直于底面,所有棱的长都为1,顶点都在同一个球面上,则该球的体积为( )
A.20π B.
C.5π D.
解析:选D 由题意知六棱柱的底面正六边形的外接圆半径r=1,其高h=1,∴球半径为R===,∴该球的体积V=πR3=×3π=.
2.(2018·镇海期中)一个棱长为6的正四面体纸盒内放一个正方体,若正方体可以在纸盒内任意转动,则正方体体积的最大值为________.
解析:由题可得,要使正方体可以在纸盒内任意转动,则只需该正方体在正四面体的内接球内即可.因为正四面体的棱长为6,所以其底面正三角形的高为3,正四面体的高为2,则该正四面体的内球的半径为,设该正方体的边长为a,要满足条件,则a≤,即a≤.所以正方体的最大体积为V=a3≤2.
答案:2
一抓基础,多练小题做到眼疾手快
1.(2018·浙江名校联考)“某几何体的三视图完全相同”是“该几何体为球”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解析:选B 由题可得,球的三个视图都是圆,所以三视图完全相同;三视图完全相同的几何体除了球,还有正方体,所以是必要不充分条件.
2.(2018·长兴中学适应性测试)一个几何体的三视图如图所示,则该几何体的体积为( )
A.64 B.72
C.80 D.112
解析:选C 由题可得,该几何体是一个棱长为4的正方体与一个底面是边长为4的正方形,高为3的四棱锥的组合体,所以其体积为V=43+×42×3=80.
3.(2019·杭二月考)一个几何体的三视图如图所示,则该几何体的体积为( )
A.π+ B.2π+
C.2π+ D.π+
解析:选A 由三视图知,该几何体的上半部分是一个三棱锥,下半部分是一个圆柱.由题图中的数据知V圆柱=π×12×1=π,三棱锥垂直于底面的侧面是边长为2的等边三角形,故其高即为三棱锥的高,故三棱锥的高为,由于三棱锥底面为一等腰直角三角形,且斜边长为2,因此两直角边长都是,则底面三角形的面积是××=1,故V三棱锥=×1×=,故该几何体的体积为π+.
4.(2018·嘉兴模拟)如图是一个几何体的三视图,若它的体积是3,则a=________,该几何体的表面积为________.
解析:由题可得,该几何体是一个水平放置的三棱柱,其底面是一个底边长为2、高为a的等腰三角形,高为3.因为其体积为3,所以V=×2a×3=3a=3,解得a=.所以该几何体的表面积为S=2××2×+2×3×3=2+18.
答案: 2+18
5.(2018·丽水模拟)若三棱锥PABC的最长的棱PA=2,且各面均为直角三角形,则此三棱锥的外接球的体积是________,表面积是________.
解析:如图,根据题意,可把该三棱锥补成长方体,则该三棱锥的外接球即该长方体的外接球,易得外接球的半径R=PA=1,所以该三棱锥的外接球的体积V=×π×13=π,表面积S=4πR2=4π.
答案:π 4π
二保高考,全练题型做到高考达标
1.圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面的半径为( )
A.7 B.6
C.5 D.3
解析:选A 设圆台较小底面半径为r,
则另一底面半径为3r.
由S=π(r+3r)·3=84π,解得r=7.
2.(2018·全国卷Ⅰ)已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( )
A.12π B.12π
C.8π D.10π
解析:选B 设圆柱的轴截面的边长为x,
则x2=8,得x=2,
∴S圆柱表=2S底+S侧=2×π×()2+2π××2
=12π.故选B.
3.(2018·温州十校联考)已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的体积是( )
A.4 B.
C.8 D.
解析:选B 由题可得,该几何体是一个底面为长方形的四棱锥,所以其体积为V=×4×2×2=.
4.(2018·兰州实战考试)一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个等腰直角三角形,则该几何体外接球的体积为( )
A.π B.
C.3π D.3
解析:选A 由题意得,该几何体为四棱锥,且该四棱锥的外接球即为棱长为1的正方体的外接球,其半径为,故体积为π3=π,故选A.
5.(2018·宁波十校联考)如图,某多面体的三视图中正视图、侧视图和俯视图的外轮廓分别为直角三角形、直角梯形和直角三角形,则该多面体的各条棱中,最长的棱的长度为( )
A.2 B.
C.2 D.
解析:选C 由题可得,该几何体是水平放置的四棱锥,其底面是一个直角梯形.所以其最长的棱的长度为=2.
6.(2018·宁波一模)某空间几何体的三视图如图所示,则该几何体的体积为( )
A.
B.
C.
D.
解析:选B 由三视图得,该几何体是从四棱锥PABCD中挖去半个圆锥后剩余的部分,四棱锥的底面是以2为边长的正方形、高是2,圆锥的底面半径是1、高是2,则所求的体积V=×2×2×2-×π×12×2=.
7.(2018·衢州调研)已知某几何体的三视图如图所示,则此几何体的体积是________;表面积是________.
解析:该几何体是一个三棱锥,其高为2,其底面是一个等腰直角三角形,腰长为,所以其体积为V=××()2×2=,表面积为S=×2×+×()2+×2×2+××=3++.
答案: 3++
8.(2018·杭州模拟)已知矩形ABCD的顶点都在半径为4的球O的球面上,且AB=3,BC=2,则棱锥OABCD的体积为________.
解析:依题意得,球心O在底面ABCD上的射影是矩形ABCD的中心,因此棱锥OABCD的高等于=,
所以棱锥OABCD的体积等于×3×2×=.
答案:
9.(2019·舟山六校联考)某四面体的三视图如图所示,其中侧视图与俯视图都是腰长为2的等腰直角三角形,正视图是边长为2的正方形,则此四面体的体积为________.
解析:由三视图可知,该四面体是四面体ABCD,如图,其中,BE⊥底面ACD,AD=DC=BE=2,则该四面体的体积为××2×2×2=.
答案:
10.(2018·武汉调研)已知正四棱锥的顶点都在同一球面上,且该棱锥的高为4,底面边长为2,则该球的表面积为________.
解析:如图,正四棱锥PABCD的外接球的球心O在它的高PO1上,设球的半径为R,为底面边长为2,所以AC=4.在Rt△AOO1中,R2=(4-R)2+22,所以R=,所以球的表面积S=4πR2=25π.
答案:25π
三上台阶,自主选做志在冲刺名校
1.(2018·广西质检)高为4的直三棱柱被削去一部分后得到一个几何体,它的直观图和三视图中的侧视图、俯视图如图所示,则该几何体的体积与原直三棱柱的体积的比值为( )
A. B.
C. D.
解析:选C 由侧视图、俯视图知该几何体是高为2、底面积为×2×(2+4)=6的四棱锥,其体积为4.易知直三棱柱的体积为8,则该几何体的体积与原直三棱柱的体积的比值为,故选C.
2.(2018·温州一模)三棱锥的三视图如图所示,则该三棱锥外接球的体积为( )
A.4π B.2π
C.4π D.2π
解析:选A 三棱锥的直观图如图,设H为三棱锥PABC外接球的球心,O1为△PAC外接圆的圆心,O2为△ABC外接圆的圆心,取AC的中点O,连接PO,HO1,O2H,HB,结合三视图易知OO1=PO=,O2B=AB=×=.∵平面PAC⊥平面ABC,HO2⊥平面ABC,HO2⊄平面PAC,∴HO2∥平面PAC,∵PO⊥平面ABC,∴OO1∥HO2,连接OO2,易知OO2∥HO1,∴四边形HO1OO2为平行四边形,∴HO2=OO1=.在Rt△HO2B中,HB==,即三棱锥PABC外接球的半径为,故所求体积为×π×()3=4π.
3.已知A,B,C是球O的球面上三点,且AB=AC=3,BC=3,D为该球面上的动点,球心O到平面ABC的距离为球半径的一半,求三棱锥D ABC体积的最大值.
解:如图,在△ABC中,
∵AB=AC=3,BC=3,
∴由余弦定理可得
cos A==-,
∴sin A=.
设△ABC外接圆O′的半径为r,
则=2r,得r=3.
设球的半径为R,连接OO′,BO′,OB,则R2=2+32,解得R=2.
由图可知,当点D到平面ABC的距离为R时,三棱锥D ABC的体积最大,
∵S△ABC=×3×3×=,
∴三棱锥D ABC体积的最大值为××3=.
相关资料
更多








