2020年高考数学一轮复习教案：第7章 第2节　空间几何体的表面积与体积(含解析)

第二节　空间几何体的表面积与体积

[考纲传真]　了解球、棱柱、棱锥、台的表面积和体积的计算公式．

1．多面体的表(侧)面积

因为多面体的各个面都是平面，所以多面体的侧面积就是所有侧面的面积之和，表面积是侧面积与底面面积之和．

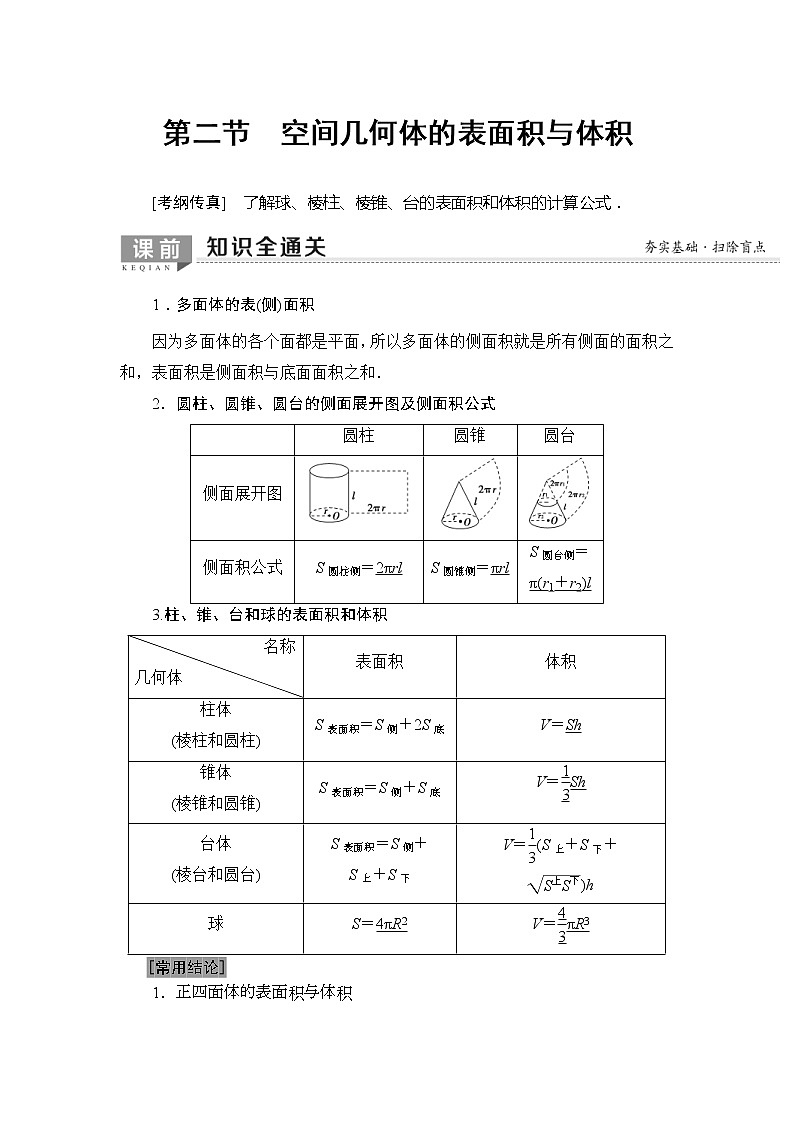
2．圆柱、圆锥、圆台的侧面展开图及侧面积公式

3.柱、锥、台和球的表面积和体积

1．正四面体的表面积与体积

棱长为a的正四面体，其表面积为a2，体积为a3.

2．几个与球有关的切、接常用结论

(1)正方体的棱长为a，球的半径为R，

①若球为正方体的外接球，则2R＝a；

②若球为正方体的内切球，则2R＝a；

③若球与正方体的各棱相切，则2R＝a.

(2)若长方体的同一顶点的三条棱长分别为a，b，c，外接球的半径为R，则2R＝.

(3)正四面体的外接球与内切球的半径之比为3∶1，棱长为a的正四面体，其内切球半径R内＝a，外接球半径R外＝a.

[基础自测]

1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”)

(1)锥体的体积等于底面面积与高之积． (　　)

(2)球的体积之比等于半径比的平方． (　　)

(3)台体的体积可转化为两个锥体的体积之差． (　　)

(4)已知球O的半径为R，其内接正方体的边长为a，则R＝a. (　　)

[答案]　(1)×　(2)×　(3)√　(4)√

2．(教材改编)已知圆锥的表面积等于12π cm2，其侧面展开图是一个半圆，则底面圆的半径为(　　)

A．1 cm　　　B．2 cm　　　C．3 cm　　　D. cm

B　[S表＝πr2＋πrl＝πr2＋πr·2r＝3πr2＝12π，∴r2＝4，

∴r＝2(cm)．]

3．圆柱的底面直径与高都等于球的直径，则球的体积与圆柱的体积比V球∶V柱为(　　)

A．1∶2         B．2∶3   C．3∶4   D．1∶3

B　[设球的半径为R.则＝＝.]

4．(教材改编)某几何体的三视图如图所示：则该几何体的体积为(　　)

A．6         B．3   C．2   D．3

B　[由三视图可知，该几何体是一个直三棱柱，其底面为侧视图，该侧视图是底边为2，高为的三角形，正视图的长为三棱柱的高，故h＝3，所以几何体的体积V＝S·h＝×3＝3.]

5．如图，将一个长方体用过相邻三条棱的中点的平面截出一个棱锥，则该棱锥的体积与剩下的几何体体积的比为________．

1∶47　[设长方体的相邻三条棱长分别为a，b，c，它截出棱锥的体积为V1＝××a×b×c＝abc，剩下的几何体的体积V2＝abc－abc＝abc，所以V1∶V2＝1∶47.]

【例1】　(1)若某空间几何体的三视图如图所示，则该几何体的表面积是(　　)

A．48＋π　　　　　 B．48－π

C．48＋2π   D．48－2π

(2)(2018·全国卷Ⅰ)已知圆柱的上、下底面的中心分别为O1，O2，过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为(　　)

A．12π          B．12π

C．8π   D．10π

(1)A　(2)B　[(1)该几何体是正四棱柱挖去了一个半球，正四棱柱的底面是正方形(边长为2)，高为5，半球的半径是1，那么该几何体的表面积为S＝2×2×2＋2×4×5－π×12＋2π×12＝48＋π，故选A.

(2)因为过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形，所以圆柱的高为2，底面圆的直径为2，所以该圆柱的表面积为2×π×()2＋2π××2＝12π.]

(1)一个四面体的三视图如图所示，则该四面体的表面积是(　　)

A．1＋          B．1＋2

C．2＋   D．2

(2)(2016·全国卷Ⅲ)如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的表面积为(　　)

A．18＋36

B．54＋18

C．90

D．81

(1)C　(2)B　[(1)由题意知题中的几何图形就是如图所示的四面体，其中AB＝AD＝CB＝CD＝，BD＝2，且平面ABD⊥平面CBD.所以△ABD与△CBD都是等腰直角三角形，而△ABC与△CAD都是边长是的等边三角形．所以表面积是×××2＋×()2×2＝2＋，故选C.

(2)由三视图可知该几何体是底面为正方形的斜四棱柱，其中有两个侧面为矩形，另两个侧面为平行四边形，则表面积为(3×3＋3×6＋3×3)×2＝54＋18.故选B.]

►考法1　公式法求体积

【例2】　(1)某几何体的三视图如图所示(单位：cm)，则该几何体的体积(单位：cm3)是(　　)

A.＋1　　　　　 B.＋3

C.＋1   D.＋3

(2)(2018·江苏高考)如图所示，正方体的棱长为2，以其所有面的中心为顶点的多面体的体积为________．

(1)A　(2)　[(1)由三视图可知该几何体是由底面半径为1，高为3的半个圆锥和三棱锥S ­ABC组成的，

如图，三棱锥的高为3，底面△ABC中，AB＝2，OC＝1，AB⊥OC.故其体积V＝××π×12×3＋××2×1×3＝＋1.故选A.

(2)正方体的棱长为2，以其所有面的中心为顶点的多面体是正八面体，其中正八面体的所有棱长都是，则该正八面体的体积为×()2×1×2＝.]

►考法2　割补法求体积

【例3】　(1)(2017·全国卷Ⅱ)如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为(　　)

A．90π          B．63π

C．42π   D．36π

(2)如图所示，在多面体ABCDEF中，已知ABCD是边长为1的正方形，且△ADE，△BCF均为正三角形，EF∥AB，EF＝2，则该多面体的体积为(　　)

A.   B.

C.   D.

(1)B　(2)A　[(1)法一：(割补法)如图所示，由几何体的三视图，可知该几何体是一个圆柱被截去上面虚线部分所得．

将圆柱补全，并将圆柱体从点A处水平分成上下两部分．由图可知，该几何体的体积等于下部分圆柱的体积加上上部分圆柱体积的，所以该几何体的体积V＝π×32×4＋π×32×6×＝63π.

故选B.

法二：(估值法)由题意，知V圆柱＜V几何体＜V圆柱．又V圆柱＝π×32×10＝90π，∴45π＜V几何体＜90π.观察选项可知只有63π符合．

故选B.

(2)法一：如图所示，分别过A，B作EF的垂线，垂足分别为G，H，连接DG，CH，则原几何体分割为两个三棱锥和一个直三棱柱，

因为三棱锥高为，直三棱柱高为1，AG＝＝，

取AD的中点M，则MG＝，

所以S△AGD＝×1×＝，

所以V＝×1＋2×××＝.

法二：如图所示，取EF的中点P，则原几何体分割为两个三棱锥和一个四棱锥，易知三棱锥P­AED和三棱锥P­BCF都是棱长为1的正四面体，四棱锥P­ABCD为棱长为1的正四棱锥．所以V＝×12×＋2×××＝.]

►考法3　等积法求体积

【例4】　如图所示，已知三棱柱ABC­A1B1C1的所有棱长均为1，且AA1⊥底面ABC，则三棱锥B1­ABC1的体积为(　　)

A.   B.

C.   D.

A　[三棱锥B1­ABC1的体积等于三棱锥A­B1BC1的体积，三棱锥A­B1BC1的高为，底面积为，故其体积为××＝.]

(1)(2019·洛阳模拟)一个几何体的三视图如图所示，则该几何体的体积为(　　)

A．2　　　　B．1   C.　　　　D.

(2)(2018·天津高考)如图，已知正方体ABCD­A1B1C1D1的棱长为1，则四棱锥A1­BB1D1D的体积为________．

(1)C　(2)　[(1)几何体如图，由三视图得底面为对角线为2的正方形，高为1，所以体积为××2×1×2×1＝，故选C.

(2)法一：连接A1C1交B1D1于点E(图略)，则A1E⊥B1D1，A1E⊥BB1，则A1E⊥平面BB1D1D，所以A1E为四棱锥A1­BB1D1D的高，且A1E＝，矩形BB1D1D的长和宽分别为，1，故VA1­BB1D1D＝×1××＝.

法二：连接BD1(图略)，则四棱锥A1­BB1D1D分成两个三棱锥B­A1DD1与B­A1B1D1，VA1­BB1D1D＝VB­A1DD1＋VB­A1B1D1＝××1×1×1＋××1×1×1＝.]

►考法1　外接球

【例5】　(1)(2017·全国卷Ⅲ)已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为(　　)

A．π　　 　B.　　 　C.　　 　D.

(2)(2018·全国卷Ⅲ)设A，B，C，D是同一个半径为4的球的球面上四点，△ABC为等边三角形且其面积为9，则三棱锥D­ABC体积的最大值为(　　)

A．12         B．18   C．24   D．54

(1)B　(2)B　[(1)设圆柱的底面半径为r，球的半径为R，且R＝1，由圆柱两个底面的圆周在同一个球的球面上可知，r，R及圆柱的高的一半构成直角三角形．

∴r＝＝.

∴圆柱的体积为V＝πr2h＝π×1＝.

故选B.

(2)如图，E是AC中点，M是△ABC的重心，O为球心，连接BE，OM，OD，BO.因为S△ABC＝AB2＝9，所以AB＝6，BM＝BE＝＝2.易知OM⊥平面ABC，所以在Rt△OBM中，OM＝＝2，所以当D，O，M三点共线且DM＝OD＋OM时，三棱锥D­ABC的体积取得最大值，且最大值Vmax＝S△ABC×(4＋OM)＝×9×6＝18.故选B.

]

►考法2　内切球

【例6】　(1)(2017·江苏高考)如图，在圆柱O1O2内有一个球O，该球与圆柱的上、下底面及母线均相切，记圆柱O1O2的体积为V1，球O的体积为V2，则的值是________．

(2)已知棱长为a的正四面体，则此正四面体的表面积S1与其内切球的表面积S2的比值为________．

(1)　(2)　[(1)设球O的半径为R，

∵球O与圆柱O1O2的上、下底面及母线均相切，

∴圆柱O1O2的高为2R，底面半径为R.

∴＝＝.

(2)正四面体的表面积为S1＝4××a2＝a2，其内切球半径r为正四面体高的，即r＝×a＝a，因此内切球表面积为S2＝4πr2＝，则＝＝.]

(1)一块石材表示的几何体的三视图如图所示，将该石材切削、打磨、加工成球，则能得到的最大球的半径等于(　　)

A．1　　　　B．2　　　　C．3　　　　D．4

(2)正四棱锥P­ABCD的侧棱和底面边长都等于2，则它的外接球的表面积是(　　)

A．16π         B．12π   C．8π   D．4π

(1)B　(2)A　[(1)由三视图可知该几何体是一个直三棱柱，底面为直角三角形，高为12，如图所示，其中AC＝6，BC＝8，∠ACB＝90°，则AB＝10.要使该石材加工成的球的半径最大，只需球与直三棱柱的三个侧面都相切，则半径r等于直角三角形ABC的内切圆半径，即r＝＝2，故能得到的最大球的半径为2，故选B.

(2)设正四棱锥的外接球半径为R，顶点P在底面上的射影为O(图略)，因为OA＝AC＝＝＝2，所以PO＝＝＝2.又OA＝OB＝OC＝OD＝2，由此可知R＝2，于是S球＝4πR2＝16π.]

1．(2016·全国卷Ⅱ)如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为(　　)

A．20π　　　　　　 B．24π

C．28π   D．32π

C　[由三视图可知，该几何体是由一个圆柱和一个圆锥组成的组合体，上面是一个圆锥，圆锥的高是2，底面半径是2，因此其母线长为4，下面圆柱的高是4，底面半径是2，因此该几何体的表面积是S＝π×22＋2π×2×4＋π×2×4＝28π，故选C.]

2．(2015·全国卷Ⅰ)《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺．问：积及为米几何？”其意思为：“在屋内墙角处堆放米(如图，米堆为一个圆锥的四分之一)，米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米约有(　　)

A．14斛          B．22斛

C．36斛   D．66斛

B　[设米堆的底面半径为r尺，则r＝8，所以r＝，所以米堆的体积为V＝×π·r2·5＝×2×5≈(立方尺)．故堆放的米约有÷1.62≈22(斛)．故选B.]

3．(2018·全国卷Ⅰ)在长方体ABCD­A1B1C1D1中，AB＝BC＝2，AC1与平面BB1C1C所成的角为30°，则该长方体的体积为(　　)

A．8          B．6

C．8   D．8

C　[连接BC1，AC1，AC.因为AB⊥平面BB1C1C，所以∠AC1B＝30°，AB⊥BC1，所以△ABC1为直角三角形．又AB＝2，所以BC1＝2.又B1C1＝2，所以BB1＝＝2，故该长方体的体积V＝2×2×2＝8.]

4．(2017·全国卷Ⅱ)长方体的长、宽、高分别为3,2,1，其顶点都在球O的球面上，则球O的表面积为________．

14π　[∵长方体的顶点都在球O的球面上，

∴长方体的体对角线的长度就是其外接球的直径．

设球的半径为R，

则2R＝＝.

∴球O的表面积为S＝4πR2＝4π×＝14π.]