冀教版23.3 方差评优课ppt课件

这是一份冀教版23.3 方差评优课ppt课件，共22页。PPT课件主要包含了学习目标等内容，欢迎下载使用。

01 知道方差是刻画数据相对于平均数的离散程度的一个统计量.
03 会用方差刻画一组数据的波动大小.
02 能正确计算一组数据的方差.
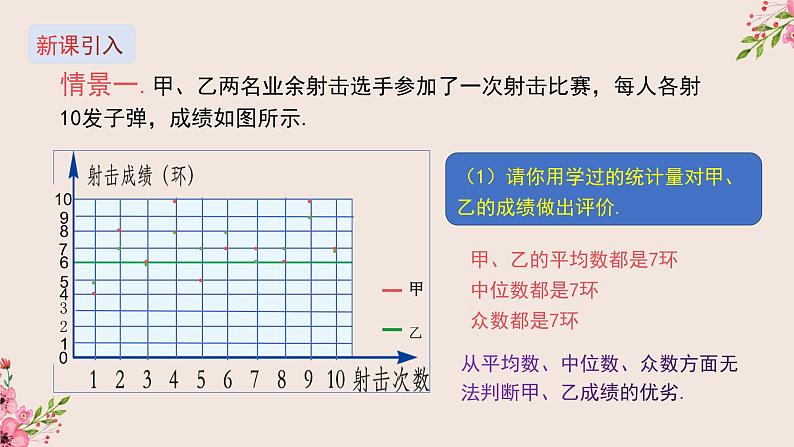
情景一.甲、乙两名业余射击选手参加了一次射击比赛，每人各射10发子弹，成绩如图所示.
（1）请你用学过的统计量对甲、乙的成绩做出评价.
甲、乙的平均数都是7环中位数都是7环 众数都是7环
从平均数、中位数、众数方面无法判断甲、乙成绩的优劣.
甲的成绩波动大，稳定性差，但有2次10环成绩，得高分概率大.
（2）两人的射击水平相同吗？说出你的看法.
乙的成绩波动小，稳定性较好，但没有10环成绩，得高分的概率小.
观点一：选甲，甲有2次10环成绩，说明甲的潜力较大，有可能夺冠.
（3）如果要从甲、乙两人中选一人去市里参加比赛，你认为应选谁？
观点二：选乙，两人平均成绩相同，乙的成绩更稳定，拿奖牌的可能性更大.
（4）如何用计算的方法得出甲的成绩波动比乙的大？
设一组数据为x1，x2，…，xn，各数据与平均数 之差的平方的平均值，叫做这组数据的方差，记做 s2。
我们计算前置中甲和乙的方差
结论：当数据分布比较分散时，方差较大，即数据波动大；当数据分布比较集中时，方差小，数据波动小.
问题一：小明的四次数学成绩分别为60,70,65,65，经计算其方差为12.5； 小红的4次数学成绩分别为80，100,100,80，经计算其方差为100.
小明的成绩比小红好，因为小明成绩的方差小，成绩稳定.
你同意这种说法吗？为什么？
注意：由于方差是刻画一组数据相对于平均数的离散程度，因此一般地，在平均数相等或很接近的前提下，比较两组数据的方差才有意义.
不同意.因为小红的平均分为90分，小明的平均分为65分，小红的成绩要远远高于小明.
问题二：甲班4名女生的身高分别为155,165,162,158 乙班4名女生的身高分别为160,160,157,163 （单位：cm）学校欲选一个班的女生参加学校的礼仪队，请你从统计学的角度，给学校提出建议.
思考：礼仪队对身高会有什么要求呢？题中考察了哪些统计量呢？
当要求整齐时，选择方差小的
问题三：学校为了选拔4名播音员，对20名学生进行了两次普通话水平测试，满分10分，测试结果如下表：
（1）利用计算器分别计算两次测试成绩的方差.
（2）那次测试结果对选拔播音员更有参考意义.
（2）方差大时，区分度更好，所以第二次测试结果更具有参考意义.
对于有选拔要求时，选择方差较大的.
1.讨论：方差越大越好吗？方差越小越好吗？
结论：方差是反映一组数据相对于平均数的离散程度.当我们需要的是一组较“整齐”的数据时，选择方差小的数据更合适；当我们需要数据有比较大的区分度，方差较大的数据更有参考意义.
注意：当一组数据的方差较大时，其平均数对数据的代表性较差，当一组数据的方差较小时，其平均数对数据的代表性较好.
2.请你在独立思考的基础上，与小组成员共同完成下列问题，并说出你的发现.
已知数据a1，a2，a3，…，an的平均数为x，方差为y, 则①数据a1+3，a2 + 3，a3 +3 ，…，an +3的平均数为--------， 方差为-------②数据a1-3，a2 -3，a3 -3 ，…，an -3的平均数为 ----------， 方差为-------- ③数据3a1，3a2 ，3a3 ，…，3an的平均数为-----------， 方差为----------. ④数据2a1-3，2a2 -3，2a3 -3 ，…，2an -3的平均数为 ----------， 方差为---------.
当一组数据中的每一个数据都加或减同一个数a，平均数也相应地加或减这一个数a，方差不变；
当一组数据中的每一个数都同时扩大或缩小为原来的a倍时，平均数也变为原来的a倍，方差变为原来的a的平方倍.
一组数据发生变化时，平均数与方差的变化规律
（1）观察图形，直接写出甲、乙这10成绩射击成绩的方差哪个大？
（2）如果其他班级参赛选手的射击成绩都在7环左右，本班应该选（ ）参赛更合适；如果其他班级参赛选手的射击成绩都在9环左右，本班应该选（ ）参赛更合适.
经计算甲和乙的平均成绩均为8环，试解决下列问题：
1.甲、乙两名战士在射击训练中，打靶的次数相同，射击成绩的平均数也相同，如果甲的射击成绩比较稳定，那么方差的大小关系是:S2甲_____S2乙。
2.已知一组数据的方差是2，如果每个数据都乘3得到组新数据，则新数据的方差是 . 。
4.绝对值小于π所有整数的方差是______.
3.已知一组数据的方差是2，如果每个数据都加3得到一新数据，则新数据的方差是 . 。
2.两组数据平均数相同或接近时比较方差，方差较大，数据波动大；方差小，数据波动小.
3.当一组数据中的每一个数据都加或减同一个数a，平均数也相应地加或减这一个数a，方差不变；当一组数据中的每一个数都同时扩大或缩小为原来的a倍时，平均数也变为原来的a倍，方差变为原来的a的平方倍.