





人教版七年级下册5.1.1 相交线优质课ppt课件
展开1. 借助两直线相交所形成的角初步理解邻补角、对顶角的概念.
2. 会根据邻补角、对顶角的性质去求一个角的度数.
3. 掌握邻补角与对顶角的性质,并能运用它们解决简单实际问题.
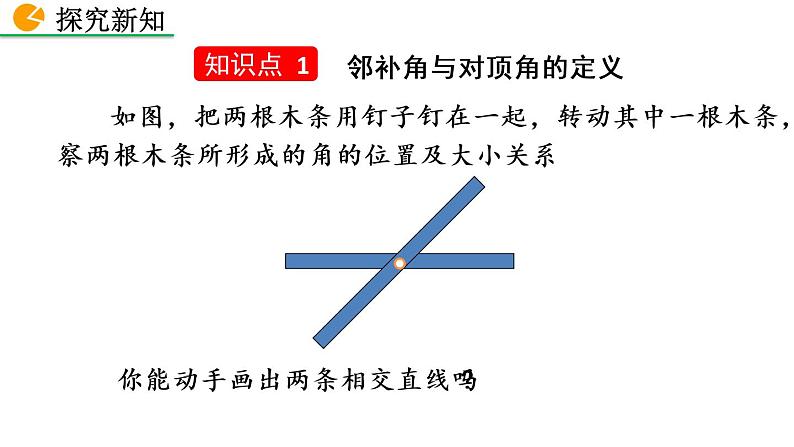
如图,把两根木条用钉子钉在一起,转动其中一根木条,观察两根木条所形成的角的位置及大小关系.
你能动手画出两条相交直线吗?
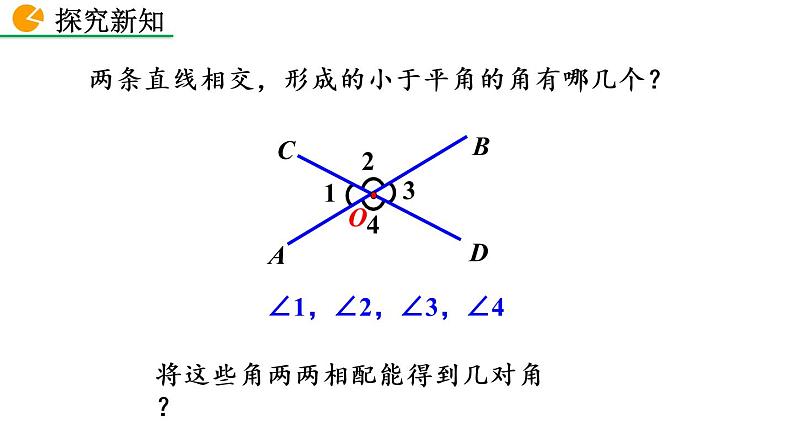
∠1,∠2,∠3,∠4
两条直线相交,形成的小于平角的角有哪几个?
将这些角两两相配能得到几对角?
你能根据这几对角的位置关系,对它们进行分类吗?
3.另一边互为反向延长线
3.两边互为反向延长线
观察∠1和∠2的顶点和两边,有怎样的位置关系?
如图,∠1与∠2有一条公共边OC,它们的另一边互为反向延长线( ∠1与∠2 互补),具有这种位置关系的两个角,互为邻补角.
类比∠1和∠2,看∠1和∠3有怎样的位置关系?
如图,∠1与∠3有一个公共顶点O,并且∠1的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
例 下列各图中,∠1与∠2是对顶角的是( )
提示:对顶角是由两条相交直线构成的,只有两条直线相交时,才能构成对顶角.
下列各组角中,∠1与∠2是对顶角的为( )
问题:∠1 与∠3在数量上又有什么关系呢?
【讨论】你能利用有关知识来验证∠1与∠3的数量关系吗?
在上学期我们已经知道互为补角的两个角的和为180°,因而互为邻补角的两个角的和为180°.
已知:直线AB与CD相交于O点(如图),求证:∠1=∠3, ∠2=∠4.
证明:∵直线AB与CD相交于O点,
∴∠1+∠2=180° ∠2+∠3=180°,
符号语言:∵直线AB与CD相交于O点, ∴∠1=∠3,∠2=∠4.
量一量:图中是对顶角量角器,你能说出用它测量角的度数的原理吗?
∠1和∠2、∠2和∠3、∠3和∠4、∠4和∠1
∠1和∠3、∠2和∠4、
考虑角的位置关系可从角的顶点和角的边入手!
例1 如图,直线a、b相交,∠1=40°,求 ∠2、∠3、∠4的度数.
变式1:若∠1= 32°20′,求∠2、∠3、∠4的度数.
解:由邻补角的定义可知
∠2=180°-∠1 =180°-40°=140°;
由对顶角相等可得
∠3=∠1=40°,∠4=∠2=140°.
利用对顶角、领补角的性质求角的度数
解:设∠1=x°,则∠2=3x°,
变式3:若∠2是∠1的3倍,求∠3的度数?
根据邻补角的定义,得 x+3x=180,
根据对顶角相等,可得∠3=∠1=45°.
变式2:若∠1+∠3 = 50°,则∠3= , ∠2= .
(3)若 1: 2 = 2: 7 ,则∠1,∠2,∠3,∠4的度数分别为________________________.
(2)若∠2是∠3的 3倍,则∠1,∠2,∠3,∠4的度数分别为________________________.
(1)若∠1+∠3= 60º ,则∠1,∠2,∠3,∠4的度数分别为________________________ .
30º 、150º 、30º、150º
45º、 135º、 45º、 135º
40º、140º、40º 、140º
如图所示,直线a和b相交于点O,完成下列各题:
例2 如图,直线AB、CD,EF相交于点O,∠1=40°,∠BOC=110°,求∠2的度数.
解:∵∠1=40°, ∠BOC=110°(已知),∴∠BOF=∠BOC-∠1 =110°-40°=70°.∵∠BOF=∠2(对顶角相等), ∴∠2=70°(等量代换).
提示:隐含条件“对顶角相等”.
利用隐含条件求角的度数
如图,直线AB、CD、EF、MN相交,若∠2=∠5,找出图中与∠2 互补的角.
解:∵ EF与AB相交,∠1+∠2=180°, ∠2+∠3= 180°,
∴∠2的补角有∠1和∠3;
∵ CD与MN相交,∠5+∠8=180°, ∠5+∠6=180 °且∠2=∠5,
∴∠2的补角有∠6和∠8;
∴∠2的补角有∠1、∠3、∠6和∠8.
如图,下列各组角中,互为对顶角的是( )A.∠1和∠2 B.∠1和∠3 C.∠2和∠4 D.∠2和∠5
1.下列各图中∠1、∠2是邻补角吗?为什么?
∠1=140° ∠1=120° ∠1=130° ∠2=40° ∠2=60° ∠2=50°
(1) (2) (3)
2.下列各图中∠1、∠2是对顶角吗?为什么?
3.如图两堵墙围一个角AOB,但人不能进入围墙,我们如何去测量这个角的大小呢?
AOB=180°-∠AOC
4.找出图中∠AOE的邻补角及对顶角,若没有请画出.
解:邻补角是∠EOB和∠AOF; 对顶角是∠BOF.
5.如图,直线AB,CD,EF相交于点O. (1)写出∠AOC, ∠BOE的邻补角; (2)写出∠DOA, ∠EOC的对顶角; (3)如果∠AOC =50°,求∠BOD ,∠COB的度数.
解:(1)∠AOC的邻补角是∠AOD和∠COB; ∠BOE的邻补角是∠EOA和∠BOF.
(2)∠DOA的对顶角是∠COB; ∠EOC的对顶角是∠DOF.
(3)∠BOD=∠AOC= 50°; ∠COB=180°-∠AOC=130°.
6.如图,直线AB,CD相交于点O, ∠EOC=70°, OA平分∠EOC,求∠BOD的度数.
解:∵OA平分∠EOC, ∴∠AOC= ∠EOC=35°, ∴∠BOD=∠AOC=35°.
如图,直线AB、CD、EF相交,若∠1 +∠5=180°,找出图中与∠1 相等的角.
解:∵∠1= ∠3(对顶角相等),
∠5+∠8=180 °且∠1 +∠5=180°,
∵∠8= ∠6(对顶角相等),
与∠1 相等的角有:∠3、∠8、∠6.
观察下列各图,寻找对顶角(不含平角)
(1)如图a,图中共有 对对顶角;(2)如图b,图中共有 对对顶角;(3) 如图c,图中共有 对对顶角;(4)研究⑴~⑶小题中直线条数与对顶角的对数之间的关系,猜测:若有n条直线相交于一点,则可形成 对对顶角;(5) 若有10条直线相交于一点,则可形成 对对顶角.
①两条直线相交形成的角;
①都是两条直线相交而成的角;
②两直线相交时,对顶角只有两对,邻补角有四对.
七年级下册5.1.1 相交线精品课件ppt: 这是一份七年级下册5.1.1 相交线精品课件ppt,共20页。PPT课件主要包含了人教版七年级下,1相交线,反向延长线,∠2∠3,邻补角,∠1和∠2互补,对顶角,∠1∠3,请大胆猜想验证,已知角等内容,欢迎下载使用。
人教版七年级下册5.1.1 相交线一等奖教学课件ppt: 这是一份人教版七年级下册5.1.1 相交线一等奖教学课件ppt,文件包含《511相交线》精品课件pptx、《511相交线》精品教学方案doc、《511相交线》精品同步习题doc等3份课件配套教学资源,其中PPT共19页, 欢迎下载使用。
人教版七年级下册5.1.1 相交线优秀ppt课件: 这是一份人教版七年级下册5.1.1 相交线优秀ppt课件,文件包含精品原创人教版数学七年级下册511《相交线》课件pptx、精品原创人教版数学七年级下册511《相交线》练习docx、精品原创人教版数学七年级下册511《相交线》教案docx等3份课件配套教学资源,其中PPT共25页, 欢迎下载使用。













