初中数学人教版九年级下册第二十六章 反比例函数26.2 实际问题与反比例函数获奖课件ppt

这是一份初中数学人教版九年级下册第二十六章 反比例函数26.2 实际问题与反比例函数获奖课件ppt，共29页。PPT课件主要包含了素养目标，吨／天，千米时，连接中考，反比例等内容，欢迎下载使用。
你吃过拉面吗？你知道在做拉面的过程中渗透着数学知识吗？
（1）体积为20cm3的面团做成拉面，面条的总长度y（单位：cm）与面条粗细（横截面积）s（单位：cm2）有怎样的函数关系？
（2）某家面馆的师傅手艺精湛，他拉的面条粗1mm2，面条总长是多少？
1. 灵活运用反比例函数的意义和性质解决实际问题.
2. 能从实际问题中寻找变量之间的关系，建立数学模型，解决实际问题.
3. 能够根据实际问题确定自变量的取值范围.
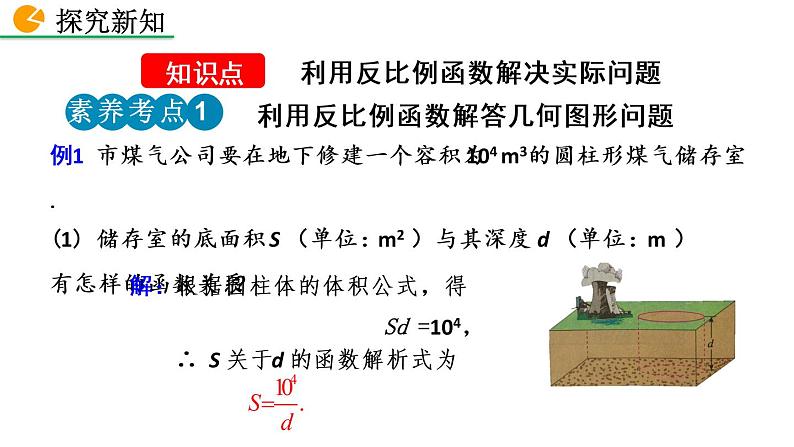
例1 市煤气公司要在地下修建一个容积为104 m3的圆柱形煤气储存室.(1) 储存室的底面积 S （单位：m2 ）与其深度 d （单位：m ）有怎样的函数关系?
解：根据圆柱体的体积公式，得 Sd =104，
∴ S 关于d 的函数解析式为
利用反比例函数解决实际问题
利用反比例函数解答几何图形问题
(2) 公司决定把储存室的底面积 S 定为 500 m2，施工队施工时应该向地下掘进多深?
解得 d = 20 （m） .如果把储存室的底面积定为 500 m²，施工时应向地下掘进 20 m 深.
(3) 当施工队按 (2) 中的计划掘进到地下 15 m 时，公司临时改变计划，把储存室的深度改为 15 m. 相应地，储存室的底面积应改为多少 (结果保留小数点后两位)?
解得 S≈666.67(m²).
当储存室的深度为15 m 时，底面积应改为 666.67 m².
第（1）问的解题思路是什么？第（2）问和第（3）问与过去所学的解分式方程和求代数式的值的问题有何联系？
方法点拨：第（1）问首先要弄清此题中各数量间的关系，然后根据圆柱的体积公式：圆柱的体积＝底面积×高，由题意知S是函数，d是自变量，改写后所得的函数关系式是反比例函数的形式.第（2）问实际上是已知函数S的值，求自变量d的取值，第（3）问则是与第（2）问相反．
我们学习过反比例函数，例如，当矩形面积一定时，长a是宽b的反比例函数，其函数关系式可以写为 （s为常数，s≠0）． 请你仿照上例另举一个在日常生活、生产或学习中具有反比例函数关系的量的实例，并写出它的函数关系式． 实例： ； 函数关系式： ．
如图，某玻璃器皿制造公司要制造一种容积为1L (1L＝1dm3)的圆锥形漏斗．（1）漏斗口的面积 S (单位：dm2)与漏斗的深 d (单位：dm) 有怎样的函数关系?
（2）如果漏斗的深为10 cm，那么漏斗口的面积为多少 dm2？
解：10cm=1dm，把 d =1 代入解析式，得 S =3.所以漏斗口的面积为 3 dm2.
(3) 如果漏斗口的面积为60 cm2，则漏斗的深为多少?
解：60 cm2 = 0.6 dm2，把 S =0.6 代入解析式，得 d =5. 所以漏斗的深为 5 dm.
例2 码头工人每天往一艘轮船上装载30吨货物，装载完毕恰好用了8天时间.(1) 轮船到达目的地后开始卸货，平均卸货速度v (单位：吨/天)与卸货天数 t 之间有怎样的函数关系?
解：设轮船上的货物总量为 k 吨，根据已知条件得k =30×8=240， 所以 v 关于 t 的函数解析式为
利用反比例函数解答运输问题
分析：根据“平均装货速度×装货天数=货物的总量”，可以求出轮船装载货物的总量；再根据“平均卸货速度=货物的总量÷卸货天数”，得到v 关于t 的函数解析式.
(2) 由于遇到紧急情况，要求船上的货物不超过5天卸载完毕，那么平均每天至少要卸载多少吨?
从结果可以看出，如果全部货物恰好用 5 天卸载完，则平均每天卸载 48 吨.而观察求得的反比例函数的解析式可知，t 越小，v 越大.这样若货物不超过 5 天卸载完，则平均每天至少要卸载 48 吨.
【讨论】题目中蕴含的等量关系是什么？我们知道“至少”对应于不等号“≥”，那么需要用不等式来解决第（2）问吗？
方法点拨：此题类似应用题中的“工程问题”，关系式为工作总量＝工作速度×工作时间，题目中货物总量是不变的，两个变量分别是速度v和时间t，因此具有反比关系．第（2）问涉及了反比例函数的增减性，即当自变量t取最大值时，函数值v取最小值．
学校锅炉旁建有一个储煤库，开学时购进一批煤，现在知道：按每天用煤0.6吨计算，一学期（按150天计算）刚好用完.若每天的耗煤量为x吨，那么这批煤能维持y天.（1）则y与x之间有怎样的函数关系？（2）画出函数图象；（3）若每天节约0.1吨，则这批煤能维持多少天？
解：（1）煤的总量为：0.6×150=90（吨）， ∵x•y=90，∴ ．（2）函数的图象为：（3）∵每天节约0.1吨煤，∴每天的用煤量为0.6-0.1=0.5（吨）， ∴ （天），∴这批煤能维持180天．
例3 一司机驾驶汽车从甲地去乙地，他以 80千米/时的平均速度用 6 小时到达乙地. （1） 甲、乙两地相距多少千米？
解：80×6=480 （千米）答：甲、乙两地相距 480 千米.
（2）当他按原路匀速返回时，汽车的速度 v 与时间 t 有怎样的函数关系？
解：由题意得 vt =480，
利用反比例函数解答行程问题
A、B两城市相距720千米，一列火车从A城去B城.（1） 火车的速度 v （千米/时） 和行驶的时间 t （时）之间的函数关系是 ．（2） 若到达目的地后，按原路匀速返回，并要求 在 3 小时内回到 A 城，则返回的速度不能低于 ．
已知一艘轮船上装有100吨货物，轮船到达目的地后开始卸货．设平均卸货速度为v（单位：吨/小时），卸完这批货物所需的时间为t（单位：小时）．（1）求 v 关于 t 的函数表达式．（2）若要求不超过5小时卸完船上的这批货物，那么平均每小时至少要卸货多少吨？
解：（1）由题意可得：100=vt，则 ；（2）∵不超过5小时卸完船上的这批货物，∴t≤5，则 ，答：平均每小时至少要卸货20吨．
2. 体积为 20 cm3 的圆柱体，圆柱体的高为 y (单位：cm） 与圆柱的底面积 S (单位：cm2） 的函数关系 ，若圆柱的底面面积为 10 mm2，则圆柱的高是 cm.
刘东家离工作单位的距离为7200 米，他每天骑自行车上班时的速度为 v 米/分，所需时间为 t 分钟．(1) 速度 v 与时间 t 之间有怎样的函数关系？
(2) 若刘东到单位用 30 分钟，那么他骑车的平均速度是多少？
解：把 t =30代入函数的解析式，得：答：他骑车的平均速度是 240 米/分.
(3) 如果刘东骑车的速度最快为 300 米/分，那他至少需要几分钟到达单位?
解：把 v =300 代入函数解析式得： 解得：t =24．答：他至少需要 24 分钟到达单位．
在某村河治理工程施工过程中，某工程队接受一项开挖水渠的工程，所需天数 y（天）与每天完成的工程量 x（ m/天） 的函数关系图象如图所示（1）请根据题意，求 y 与 x 之间的函数表达式；
(2) 若该工程队有 2 台挖掘机，每台挖掘机每天能够开挖水渠 15 m，问该工程队需用多少天才能完成此项任务？
解：由图象可知共需开挖水渠 24×50=1200 (m)， 2 台挖掘机需要 1200÷(2×15)=40 (天).
(3) 如果为了防汛工作的紧急需要，必须在一个月内 (按 30 天计算)完成任务，那么每天至少要完成多少 m？
解：1200÷30=40 (m)， 故每天至少要完成40 m．
实际问题中的反比例函数
过程：分析实际情境→建立函数模型→明确数学问题
注意：实际问题中的两个变量往往都只能取非负值；作实际问题中的函数图象时，横、纵坐标的单位长度不一定相同.